- 「固有値」「固有ベクトル」「寄与率」…似た言葉が多すぎて混乱
- 公式は覚えたけど、「なぜこの式なの?」がわからない
- 計算はできても、結果の「意味」が説明できない
- 4つの用語の違いが「宝探し」のたとえでスッキリわかる
- 公式の意味をイメージで説明できるようになる
- QC検定1級の計算問題が自信を持って解ける
目次
まず全体像をつかもう|4つの用語の関係マップ
いきなり個別の用語を覚えようとすると混乱します。まずは「4つの用語がどう関係しているか」を見てみましょう。
主成分分析は「宝探しゲーム」に似ています。

| ①固有ベクトル | 🧭 コンパス = どの方向に宝がある? |
| ②固有値 | 💰 宝の量 = その方向にどれだけ宝がある? |
| ③寄与率 | 🥧 パイの取り分 = 全体の何%の宝? |
| ④累積寄与率 | 📊 積み上げ合計 = ここまでで何%集まった? |
この関係を頭に入れてから、それぞれの用語を見ていきましょう。
用語①:固有ベクトル|「どの方向に宝がある?」を示すコンパス
宝探しをするとき、最初に必要なのは「どの方向に進めばいいか」ですよね。
固有ベクトルは、まさにその「方向を示すコンパス」の役割をします。

固有ベクトル = データが一番「広がっている方向」を指す矢印
データを散布図にプロットすると、点の集まりは楕円形に広がることが多いです。
その楕円の「長い方向」が第1固有ベクトル、「短い方向」が第2固有ベクトルになります。
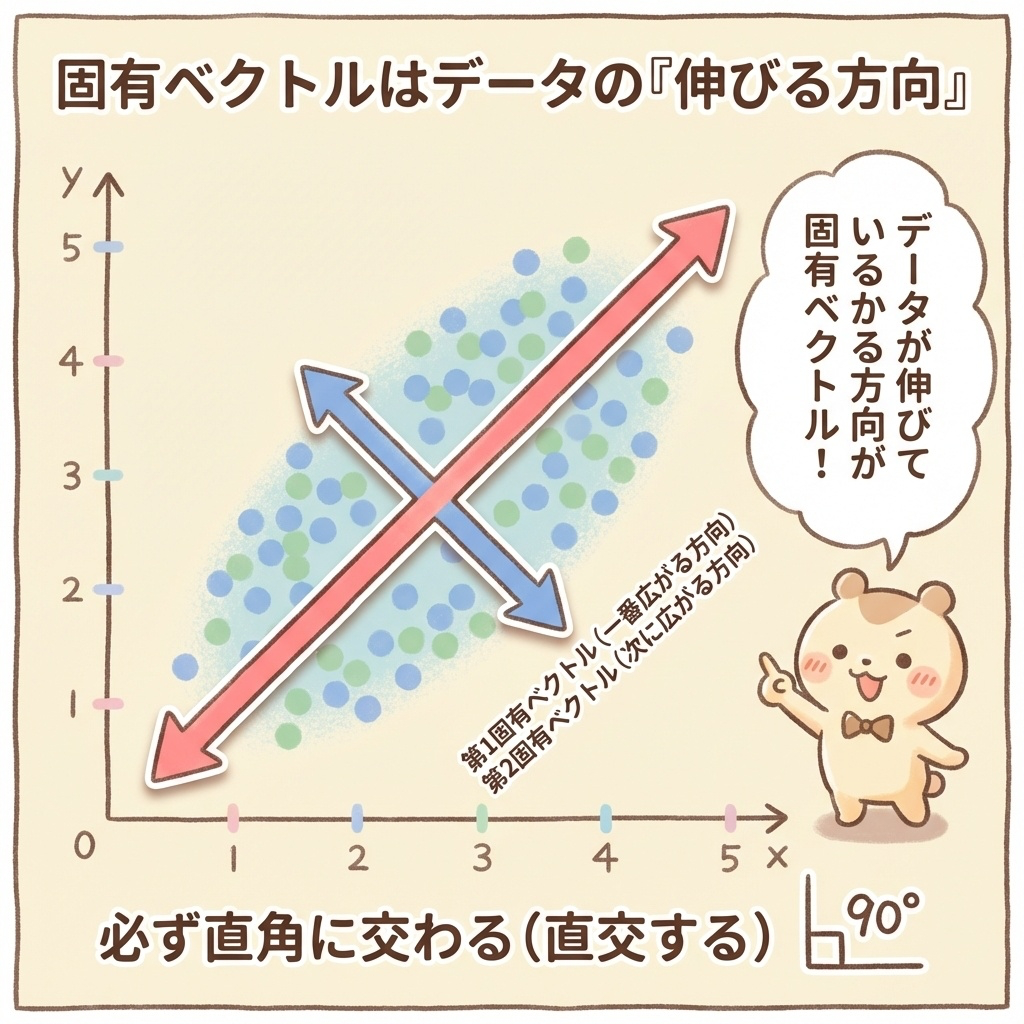
固有ベクトルの重要な性質|必ず直角に交わる
固有ベクトルには大事な性質があります。
固有ベクトル同士は必ず直角(90°)に交わる。
これを「直交する」と言います。
なぜ直角なのか?それは、「すでに説明した方向とは違う情報を取り出すため」です。
第1主成分で「東西方向の広がり」を見たなら、第2主成分では「南北方向の広がり」を見る。同じ方向を2回見ても意味がないですよね。
用語②:固有値(λ)|「その方向にどれだけ宝がある?」
固有ベクトルが「方向」を示すなら、固有値は「その方向にある宝の量」です。

固有値 = その方向にデータがどれだけ広がっているか(分散)
同じ距離を歩いても、方向によって見つかる宝の量は違います。
データも同じ。ある方向から見るとデータが大きく広がって見え(固有値が大きい)、別の方向から見ると狭くまとまって見える(固有値が小さい)。
なぜ「固有値=分散」なの?|イメージで理解する
これはとても大事なポイントです。
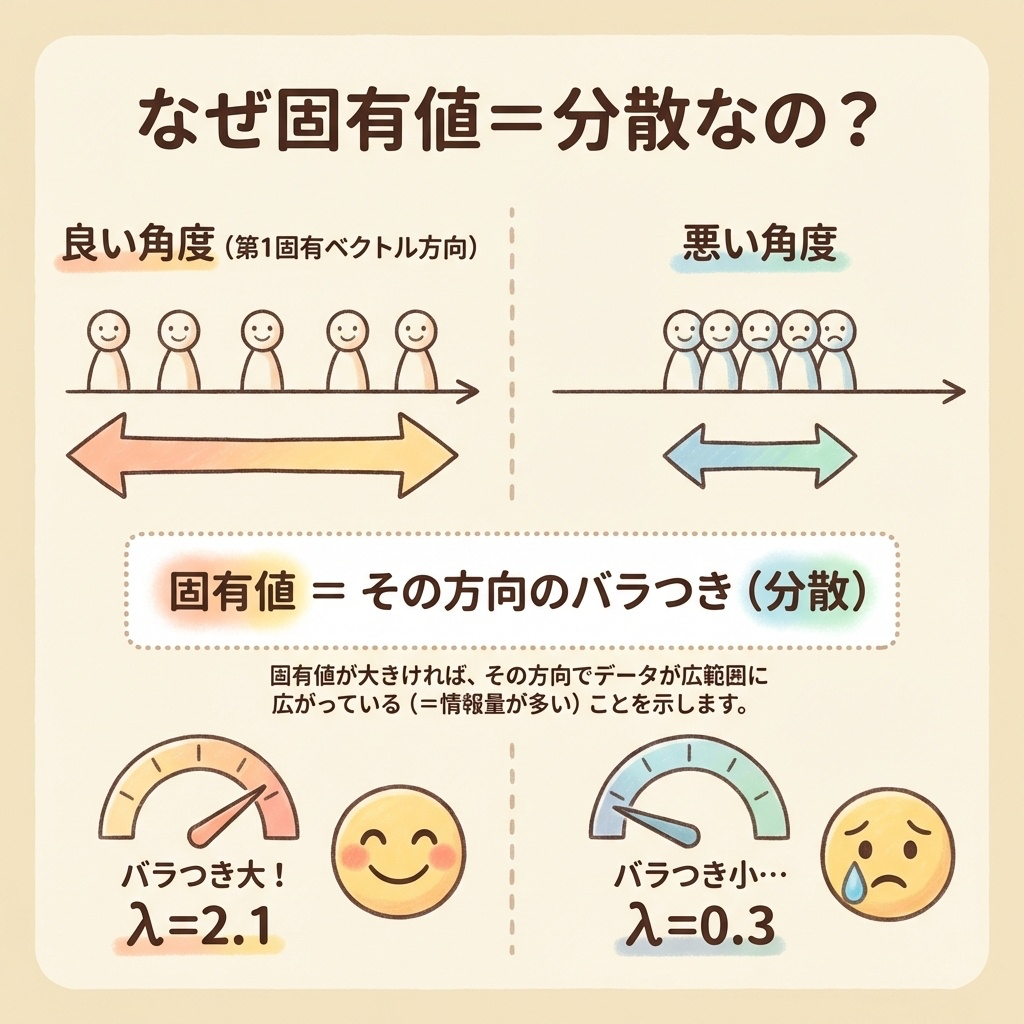
5人を一列に並べて写真を撮ることを想像してください。
良い角度から撮ると、5人がバラバラに広がって見える(バラつき=分散が大きい)。
悪い角度から撮ると、5人が重なって見える(バラつき=分散が小さい)。
この「バラつきの大きさ」が固有値です。だから固有値=分散なのです。
固有値(λ)= その主成分の分散 = Var(Z)
これはQC検定で必ず出る公式です!
固有ベクトルと固有値はセット!|方向と大きさ
ここで大事なことを確認しましょう。

| 用語 | 役割 | 宝探しで例えると |
|---|---|---|
| 固有ベクトル | 方向を示す | 🧭 コンパス「北へ進め!」 |
| 固有値 | 大きさを示す | 💰 宝箱「2.1kg分の金貨!」 |
この2つは必ずペアで登場します。「どの方向に」「どれだけの情報があるか」を一緒に表しているからです。
固有値の大きさで重要度がわかる
固有値を大きい順に並べると、主成分の重要度ランキングになります。

例えば、3つの変数で主成分分析をした結果:
| 順位 | 主成分 | 固有値(λ) | 解釈 |
|---|---|---|---|
| 🥇 | 第1主成分 | 2.1 | 一番重要! |
| 🥈 | 第2主成分 | 0.7 | 2番目に重要 |
| 🥉 | 第3主成分 | 0.2 | あまり重要でない |
でも、「2.1」「0.7」「0.2」という数字だけ見ても、「全体の中でどれくらい重要なの?」がわかりにくいですよね。
そこで登場するのが寄与率です。
用語③:寄与率|「全体の何%の宝?」パイの取り分
寄与率は、「その主成分が全体の情報のうち何%を占めているか」を表します。
ホールケーキ(パイ)を切り分けるイメージです。

寄与率 = その主成分が「全体の宝」の何%を持っているか
寄与率の公式|なぜこの式になるの?
- λᵢ:その主成分の固有値(自分の宝)
- Σλ:全部の固有値の合計(全部の宝)
この公式、難しそうに見えますが、実は小学校で習う「割合」の計算と同じです。

【日常の例】クラス30人のうち、赤い服を着ている人は21人。割合は?
→ 21 ÷ 30 × 100% = 70%
【寄与率】全部の固有値の合計が3.0で、第1主成分の固有値が2.1。割合は?
→ 2.1 ÷ 3.0 × 100% = 70%
考え方は全く同じです!「全体のうち、どれだけの割合か」を計算しているだけ。
寄与率の計算を実際にやってみよう
先ほどの例(λ₁=2.1, λ₂=0.7, λ₃=0.2)で計算してみましょう。

Step 1:全部の固有値を足す
Σλ = 2.1 + 0.7 + 0.2 = 3.0
Step 2:それぞれの固有値を合計で割って×100%
- 第1主成分:2.1 ÷ 3.0 × 100% = 70%
- 第2主成分:0.7 ÷ 3.0 × 100% = 23%
- 第3主成分:0.2 ÷ 3.0 × 100% = 7%
Step 3:確認(全部足すと100%になるか?)
70% + 23% + 7% = 100% ✓ OK!
寄与率を全部足すと必ず100%になります。
もし100%にならなかったら、どこかで計算ミスしています!
用語④:累積寄与率|「ここまでで何%集まった?」
累積寄与率は、第1主成分から順番に寄与率を足し算していった合計です。
コインを積み上げていくイメージで考えましょう。

累積寄与率 = 上から順に寄与率を足していった合計(%)
累積寄与率の計算|足し算するだけ!
| 主成分 | 固有値(λ) | 寄与率 | 累積寄与率 | 計算方法 |
|---|---|---|---|---|
| 第1 | 2.1 | 70% | 70% | 70% |
| 第2 | 0.7 | 23% | 93% ✓ | 70% + 23% |
| 第3 | 0.2 | 7% | 100% | 70% + 23% + 7% |
累積寄与率の使い方|「何個の主成分を使う?」の判断基準
累積寄与率の一番大事な使い方は、「何個の主成分を採用するか」を決めることです。

累積寄与率が 80% を超えたら、そこでストップ!
上の例では、第2主成分までで累積寄与率93%なので、2つの主成分で十分です。
第3主成分(7%)は無視しても、ほとんど情報を失いません。
問題によっては「80%以上」「70%以上」「90%以上」など基準が指定されることがあります。
問題文をよく読んで、指定された基準を使いましょう!
実践!QC検定で出る計算問題を解いてみよう
ここまでの知識を使って、実際の問題を解いてみましょう。

5つの変数について主成分分析を行ったところ、以下の固有値が得られた。
λ₁=2.5, λ₂=1.2, λ₃=0.8, λ₄=0.3, λ₅=0.2
(1) 各主成分の寄与率を求めよ
(2) 累積寄与率が80%を超えるのは第何主成分までか
解答の手順
Step 1:固有値の合計を計算
Σλ = 2.5 + 1.2 + 0.8 + 0.3 + 0.2 = 5.0
Step 2:各主成分の寄与率を計算
| 主成分 | 固有値(λ) | 寄与率の計算 | 寄与率 | 累積寄与率 |
|---|---|---|---|---|
| 第1 | 2.5 | 2.5÷5.0×100% | 50% | 50% |
| 第2 | 1.2 | 1.2÷5.0×100% | 24% | 74% |
| 第3 | 0.8 | 0.8÷5.0×100% | 16% | 90% ✓ |
| 第4 | 0.3 | 0.3÷5.0×100% | 6% | 96% |
| 第5 | 0.2 | 0.2÷5.0×100% | 4% | 100% |
(1) 寄与率:第1=50%, 第2=24%, 第3=16%, 第4=6%, 第5=4%
(2) 累積寄与率が80%を超えるのは第3主成分まで(累積90%)
よくある間違い3選|ここで点を落とさない!

間違い:λ₁ ÷ λ₂ = 2.1 ÷ 0.7 = 3.0
正解:λ₁ ÷ Σλ(全部の合計) = 2.1 ÷ 3.0 = 0.7 → 70%
分母は必ず「全部の固有値の合計」です!
間違い:2.1 ÷ 3.0 = 0.7(単位なし)
正解:2.1 ÷ 3.0 × 100 = 70%
寄与率はパーセント(%)で表します!
固有ベクトル = 方向(コンパス)「どっちに進む?」
固有値 = 大きさ(宝の量)「どれだけある?」
全く別物です!名前が似ているので注意!
まとめ|4つの用語を完全マスター!
| 用語 | イメージ | 公式・意味 | 覚え方 |
|---|---|---|---|
| 固有ベクトル | 🧭 コンパス | データが広がる方向 | 直角に交わる! |
| 固有値(λ) | 💰 宝箱 | λ = 分散 = 情報量 | 大きいほど重要! |
| 寄与率 | 🥧 パイの取り分 | λᵢ ÷ Σλ × 100% | 全部で100%! |
| 累積寄与率 | 📊 積み上げ | 上から順に足す | 80%超えでOK! |
- 固有ベクトルと固有値はセット(方向と大きさ)
- 寄与率は「割合を%で出す」いつもの計算と同じ
- 累積寄与率80%を超えたら、そこで主成分数を決定
- 計算したら合計100%になるか確認!
📚 次に読むべき記事
主成分の「意味」を解釈する方法を学ぶ。寄与率の次はこれ!
各データの「新しい成績表」を計算する方法を解説。
固有値・固有ベクトルの数学的な導出を詳しく学びたい方はこちら。
主成分分析を徹底解説!データを効率的に分析する3つの目的 →
【完全版】統計学の勉強ロードマップ|初心者が「データ分析」を武器にするまでの全手順 →
