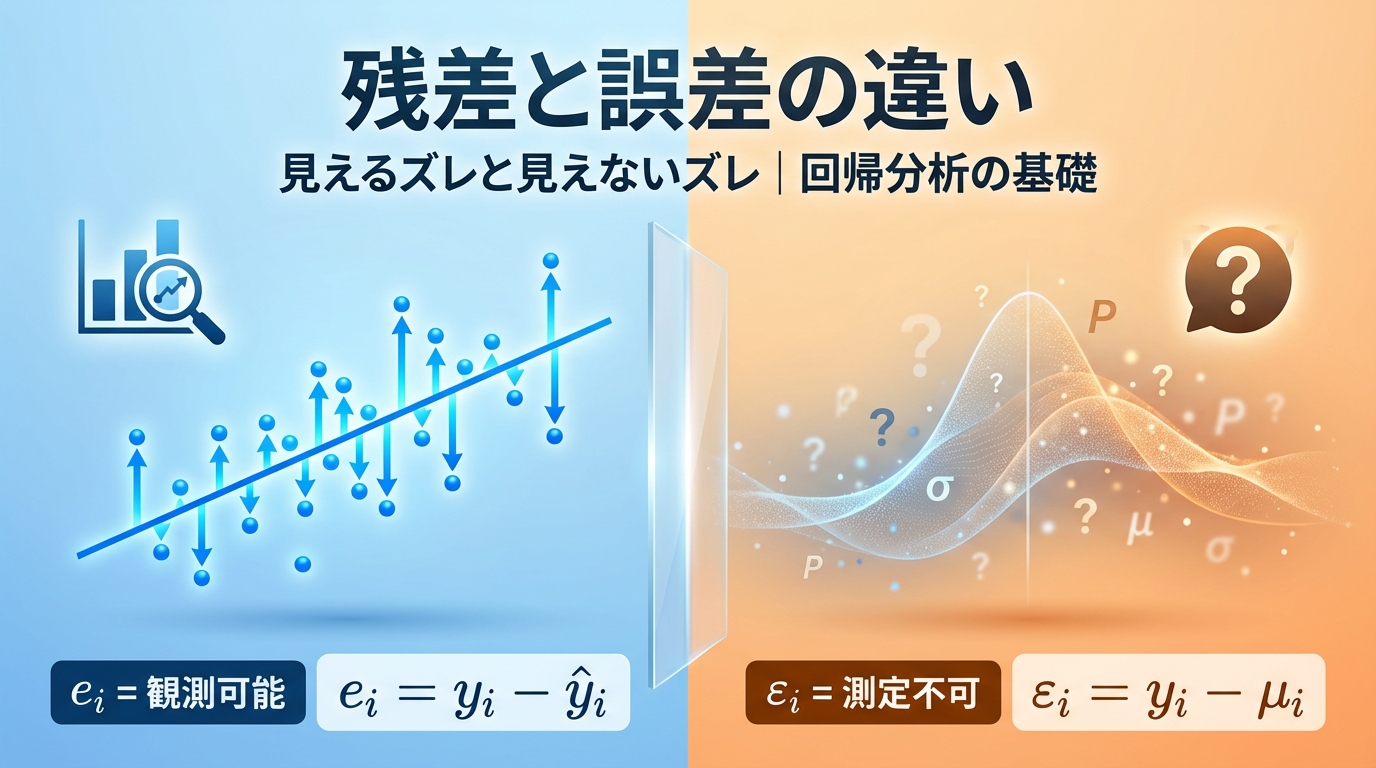
「残差」と「誤差」、どちらも「ズレ」を表す言葉ですが、実はまったく違う世界を見ています。
📊 残差 = 手元のデータで計算できる「見えるズレ」
❓ 誤差 = 理論上の概念で計算できない「見えないズレ」
この違いを理解すれば、回帰分析の精度が劇的にアップします!
📌 この記事で分かること
- 残差と誤差の決定的な違いを一枚の図で理解
- 残差の計算方法を3ステップで完全マスター
- 残差プロットでモデルの問題点を診断する方法
- 誤差の4つの仮定と残差を使った確認方法
回帰分析を勉強していると、必ず出てくる2つの用語があります。
それが「残差(Residual)」と「誤差(Error)」です。
「モデルの当てはまりを確かめるために残差を見ましょう」と聞いて、
「それって"誤差"と同じじゃないの?」と感じたことはありませんか?
💡 実はこの2つ、見ている世界が違うので、混同すると理解が一気に難しくなります。
この記事では、統計学において超重要なこの2つの概念を、初心者でも完全に理解できるよう、図解をたっぷり使って徹底解説します。
目次
残差と誤差の違いを一枚で理解
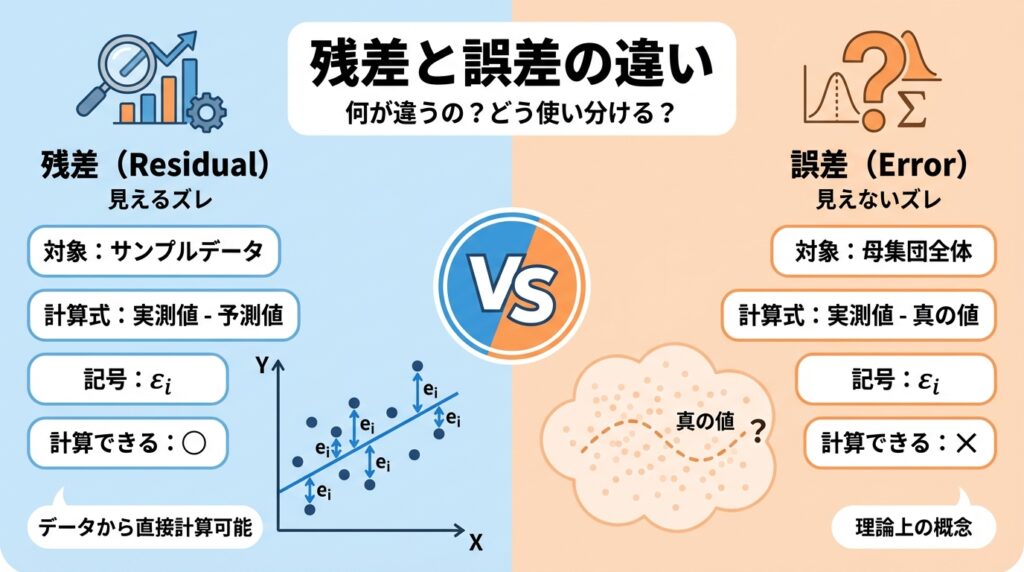
まずは、残差と誤差の違いを一覧表で整理しましょう。
この表を見れば、2つの概念がどう違うのか一目瞭然です。
💡 ポイント
- 残差は「観測できるズレ」で、実際に計算できる
- 誤差は「理想の世界と現実のズレ」で、直接は測れない
- 残差は誤差の"見える化"に相当し、解析後の健康診断に使う
つまり、残差は「見える世界」、誤差は「見えない世界」なのです。
でも、残差を調べることで、見えない誤差の性質を推測できるというわけですね!
☕ コーヒーブレイク
「誤差」は英語で"Error"ですが、これは「間違い」という意味ではありません。
むしろ「モデルでは説明しきれない、ランダムな要因」を指します。
だから、誤差があること自体は悪いことではないんです!
残差が生まれるまで:3ステップでイメージ
それでは、残差がどうやって生まれるのかを、具体例を使って3ステップで見ていきましょう。
ここでは、「勉強時間」と「テスト点数」の関係を分析する例を考えます。
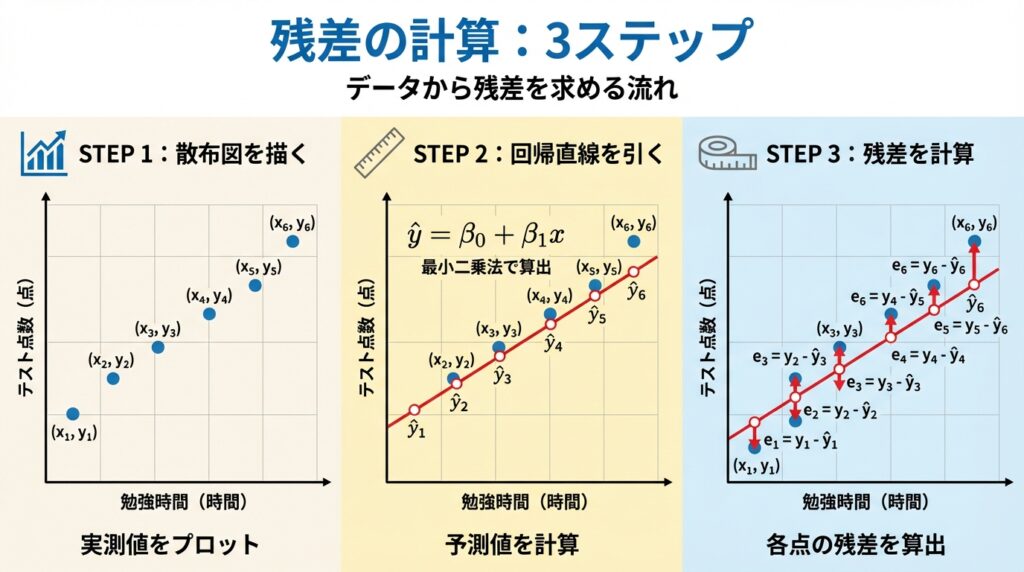
📈 STEP 1:散布図を描く
まず、横軸に勉強時間(x)、縦軸にテスト点数(y)をとって、データの点をプロットします。
点の「雲」を観察すると、右肩上がりの関係がありそうだと感覚的につかめますね。
📐 STEP 2:回帰直線を引く
次に、最小二乗法を使って、データに最もよく当てはまる直線を引きます。
ŷ = β0 + β1x
この直線が「予測モデル」になります。
ここまでが"モデル作り"の段階です。
📏 STEP 3:残差を計算
各データ点について、以下の式で残差(ei)を計算します。
ei = yi − ŷi
(実測値 − 予測値 = 残差)
図を見ると、縦方向の短い矢印が残差を表しています。
矢印が上下に散っていれば、モデルにまだ吸収しきれない要因が潜んでいる合図です。
🔍 残差の意味を深掘り
- プラスの残差:実測値が予測値より上(モデルが過小評価)
- マイナスの残差:実測値が予測値より下(モデルが過大評価)
- ゼロに近い残差:予測が的中!
残差プロットで分かる4つのこと
残差を計算したら、次は「残差プロット」を作ります。
これは、横軸に予測値(ŷ)、縦軸に残差(e)をとった散布図です。
このプロットを見れば、モデルの問題点が一目瞭然になります!
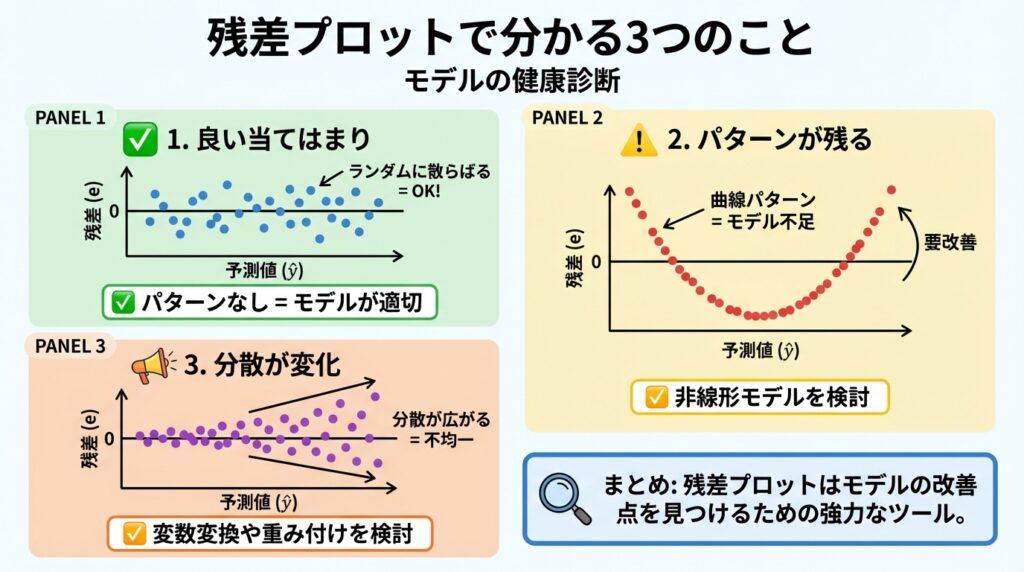
✅ 1. モデルの当てはまり
残差がランダムに散らばっているなら、モデルは良い当てはまりを示しています。
逆に、残差に曲線的なパターンが見えるなら、直線モデルでは不十分かもしれません。
その場合は、非線形モデル(2次関数など)を検討しましょう。
⚠️ 2. パターンの検出
残差プロットにU字型やS字型のパターンが現れたら要注意。
これは、モデルが重要な非線形関係を見逃している可能性があります。
⚠️ 対処法:変数変換(対数変換、平方根変換など)や、多項式回帰を試してみましょう。
📢 3. 等分散性の確認
残差の散らばり具合が、予測値に関わらず一定かをチェックします。
もし、予測値が大きくなるにつれて残差の散らばりも大きくなる「漏斗(ろうと)型」になっていたら、等分散性の仮定が破れています。
🚨 対処法:加重最小二乗法や、変数変換を検討しましょう。
🎯 4. 外れ値の検出
他の点から大きく飛び出した残差は、外れ値の候補です。
外れ値は、データ入力ミスの可能性もあれば、重要な特殊ケースの可能性もあります。
クック距離などで影響の大きさを数値化し、慎重に判断しましょう。
💡 ワンポイントアドバイス
外れ値を見つけたら、すぐに削除するのではなく、「なぜこのデータが外れているのか?」を考えましょう。
ビジネス的に意味がある点なら、残す判断も重要です!
誤差の4つの仮定と残差を使った確認方法
回帰分析では、「誤差(ε)」に関する4つの仮定を置いています。
これらの仮定が満たされていないと、推定結果が信頼できなくなります。
でも安心してください!残差を調べることで、誤差の性質を推測できます。
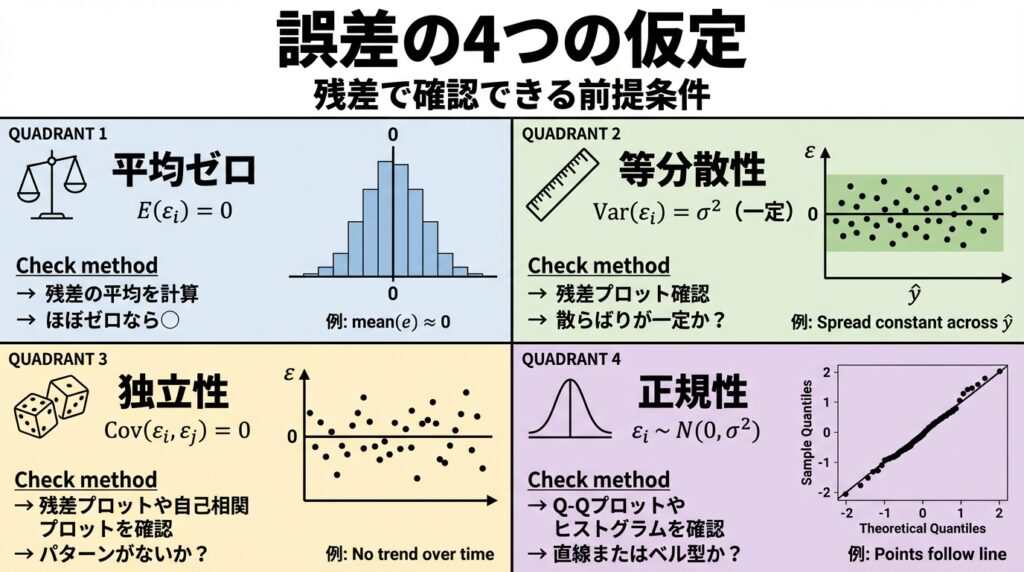
💡 重要なポイント
残差は誤差の"代理"なので、残差を調べれば誤差の性質が分かります!
ただし、サンプルサイズが小さいと判断が難しいので、できるだけ多くのデータを集めましょう。
よくある誤解と正しい見方
残差と誤差について、初心者がよく陥る誤解をまとめました。
あなたも当てはまっていませんか?
まとめ:残差は"モデルの健康診断レポート"
📝 この記事のまとめ
- 残差は「データ」と「モデル予測」のズレを数値化した"健康診断レポート"
- 誤差は未知の真のモデルとのズレで直接は測れないが、残差を通じて姿を推測できる
- 残差プロットでパターン・分散・外れ値をチェックすれば、モデルの問題点が見える
- 誤差の4つの仮定を残差で確認することで、信頼できる推定結果が得られる
- 残差を活かせば、モデルの説得力と予測精度が大幅アップ!
残差と誤差の違い、理解できましたか?
この知識があれば、回帰分析の精度を格段に高めることができます。
次は、実際に残差プロットを作って、あなたのモデルを診断してみましょう!
🔗 あわせて読みたい関連記事
📊 単回帰分析の基礎
回帰分析の基本をゼロから学ぶならこちら
記事を読む →
📈 決定係数(R²)の見方
モデルの当てはまりを数値で評価
記事を読む →
🎯 外れ値の検出と対処
データの異常値をどう扱うか
記事を読む →
📚 統計学をもっと学びたいあなたへ
当サイトでは、統計学の基礎から実践まで、初心者でも分かりやすく解説しています。
ぜひ他の記事もチェックしてみてください!