こんにちは、シラスです。
統計を勉強していると、ふと奇妙なことに気づきませんか?
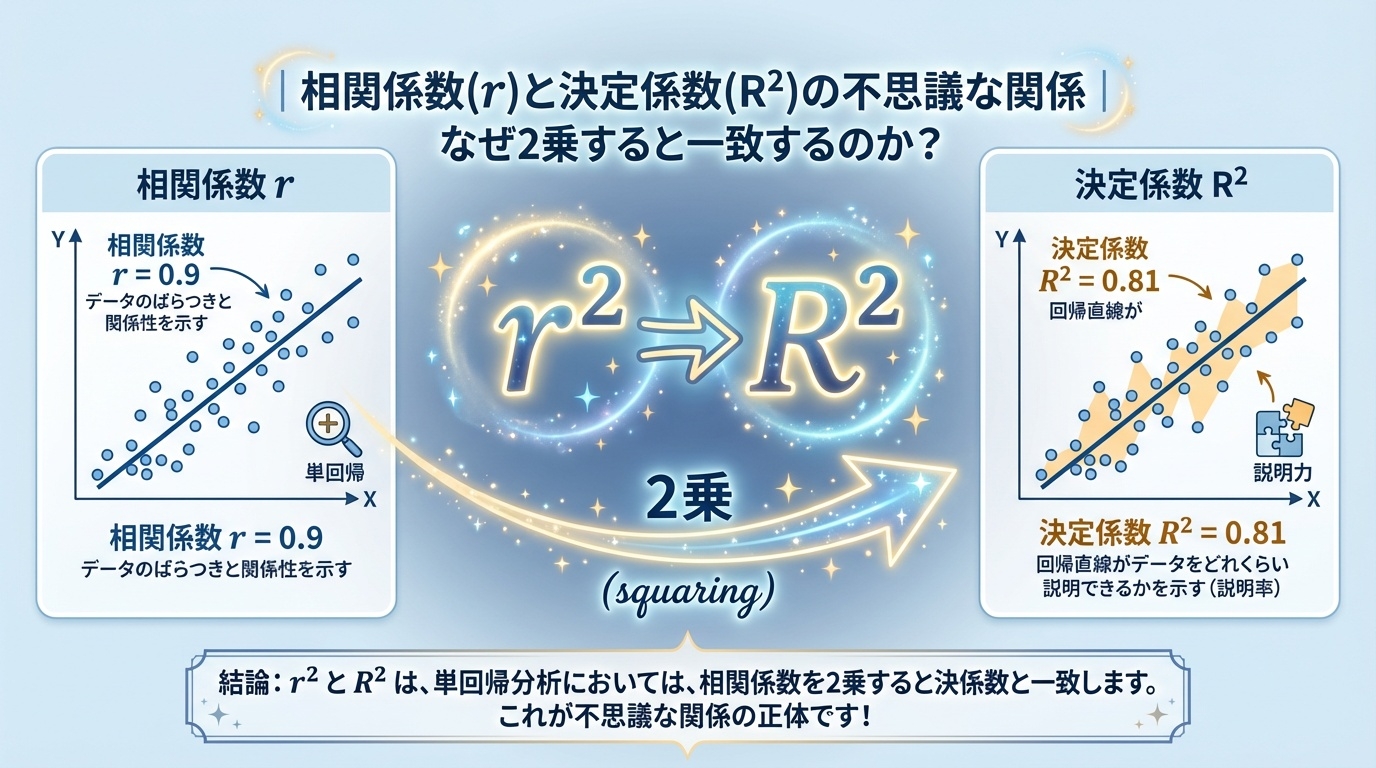
相関係数 $r$ を2乗すると、
なぜか決定係数 $R^2$ と同じ数字になる。
例えば、相関係数が $0.9$ なら、決定係数は $0.9 \times 0.9 = 0.81$。
これは偶然ではありません。実は、単回帰分析(1対1の関係)においてのみ成立する、数学的な魔法なのです。
今回は、なぜこの2つが繋がっているのか、その「数学的な正体」を視覚的に紐解きます。
1. まずは「記号」で納得する
難しい理屈の前に、記号の見た目を見てみましょう。
統計学者がこの記号を選んだ時点で、答えは書いてあります。
相関係数 $r$ には「プラスとマイナス」があります(右上がりか、右下がりか)。
しかし、決定係数 $R^2$ は「予測がどれくらい当たっているか(精度)」の話なので、右上がりだろうが右下がりだろうが関係ありません。
だから、2乗してプラスマイナスの情報を消してしまうのです。
2. 数学的な理由:「標準化」の世界
ここからが本題です。なぜピッタリ一致するのでしょうか?
その鍵は、データを扱いやすくする「標準化(平均0、分散1に変換すること)」にあります。
あらゆるデータを標準化された世界(単位のない世界)に連れて行くと、驚くべきことが起きます。
① 回帰直線の「傾き」が、そのまま相関係数 $r$ になる。
通常、$y = ax+b$ の傾き $a$ は複雑な計算が必要ですが、標準化すると、なんと「傾き = $r$」になります。
② 決定係数 $R^2$ は、「傾き」の2乗で求まる。
この世界では、分散(データの広がり)が「1」です。
数学的に、「説明できた分散」は「(傾き)² × (Xの分散)」になります。
Xの分散は1なので、決定係数 = (傾き)² になります。
💡 つまり、こういうこと!
論理をつなげると、こうなります。
※あくまで「単回帰分析(xとyが1つずつ)」の場合に限ります。
3. 直感イメージ:重なり具合
数式が苦手な方は、このイメージだけ持ち帰ってください。
相関係数とは、2つのデータが「どれくらい同じ方向を向いているか」を表す矢印のようなものです。
-
相関係数 ($r$):
データの「結びつきの強さ」そのもの。
例:身長と体重はかなり強く結びついている ($r=0.7$) -
決定係数 ($R^2$):
その結びつきを使って「どれくらい説明できるか」というパワー。
例:結びつき($0.7$)を2回掛けると、説明力($0.49$)になる。
なぜ2回掛けるのか?
それは、「確率」のようなものだからです。「あやふやさ($r$)」が2つ重なると、説明できる範囲($R^2$)は掛け算で小さくなるのです。
まとめ
Excelで分析するとき、「相関が0.8もある!」と喜んでも、決定係数で見ると「0.64(64%しか説明できていない)」と冷静になれるのは、この「2乗の法則」があるからなのです。