- 偏回帰係数が有意なのはわかった。でも「5.0」ってどのくらい信頼できるの?
- 信頼区間って聞いたことあるけど、どう計算するの?
- 95%信頼区間の「95%」って何を意味してるの?
- 区間推定が「点推定」より優れている理由
- 95%信頼区間の計算方法を具体的な数値例で完全理解
- 信頼区間から「有意かどうか」も判定できる裏技
「広告費の偏回帰係数は5.0で、有意だった。じゃあ、広告費を1万円増やすと売上は5万円増えるんだね?」
…ちょっと待ってください。
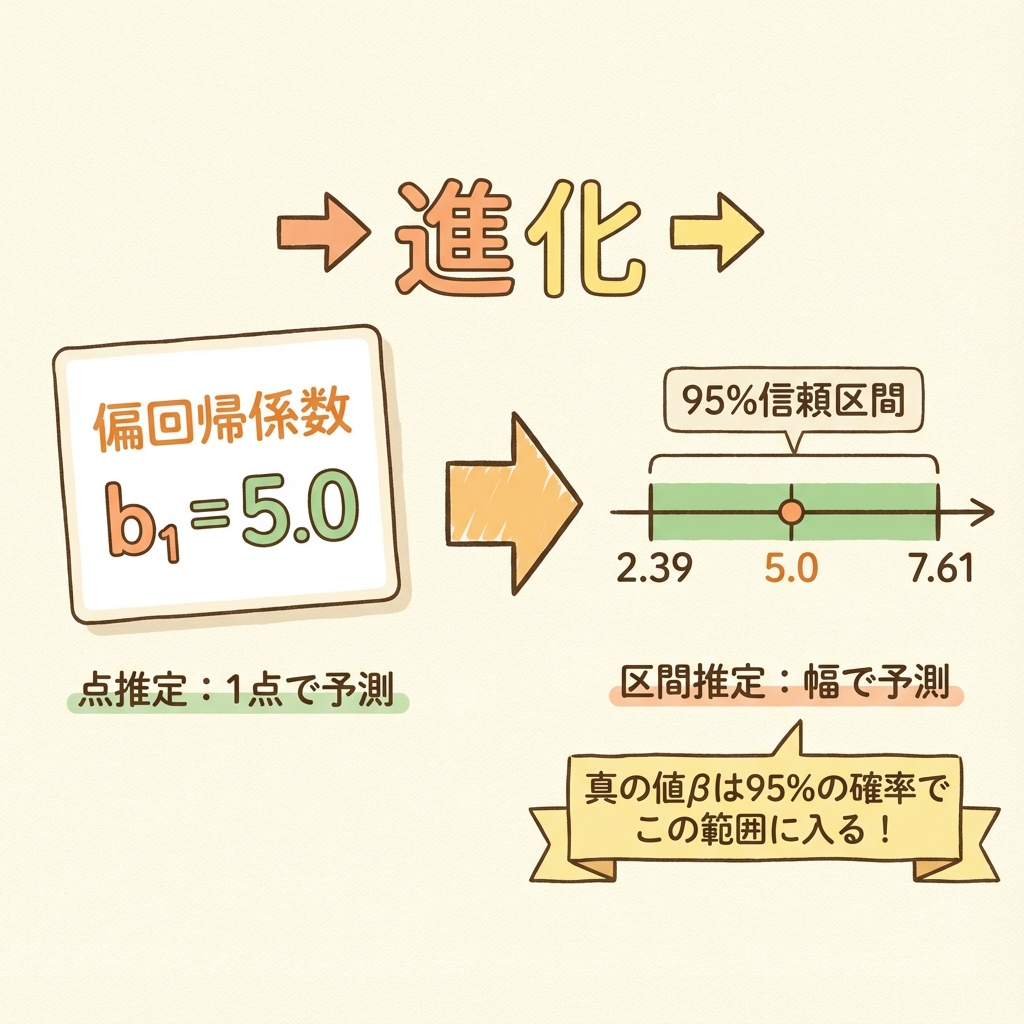
その「5.0」はサンプルから計算した推定値です。別のサンプルで計算したら「4.0」かもしれないし「6.0」かもしれません。
つまり、「5.0」という1点だけを信じるのは危険なんです。
そこで登場するのが「区間推定」です。
区間推定を使えば、「真の偏回帰係数βは、95%の確率で2.39〜7.61の範囲にある」といった形で、推定の"幅"を示すことができます。
この記事では、偏回帰係数の信頼区間の考え方から計算方法まで、具体的な数値例を使って徹底解説します。
目次
なぜ「点推定」だけでは不十分なのか?
点推定の限界|「当たり」か「外れ」かの二択になってしまう
偏回帰係数 b = 5.0 という値は、「点推定」と呼ばれます。
点推定とは、母集団のパラメータ(真の値β)を1つの値で推定すること。ダーツの的に向かって「ここだ!」と1点を狙うイメージです。
でも、よく考えてみてください。
ダーツの的の中心(真の値β)に、ピッタリ当たる確率ってどのくらいでしょう?
…ほぼゼロですよね。
点推定では、「真の値βがちょうど5.0である確率」は限りなくゼロに近いのです。
点推定だけでは、推定の「不確かさ」がわかりません。
「5.0」という値が…
・ほぼ確実に正しいのか?(4.9〜5.1くらい?)
・かなり不確かなのか?(1.0〜9.0くらい?)
…これがわからないと、ビジネス判断に使えませんよね。
区間推定の発想|「網」を張って真の値を捕まえる
そこで登場するのが「区間推定」です。
区間推定とは、母集団のパラメータ(真の値β)を「幅」で推定すること。ダーツの的に「網」を張って、「この範囲のどこかに真ん中がある」と言うイメージです。
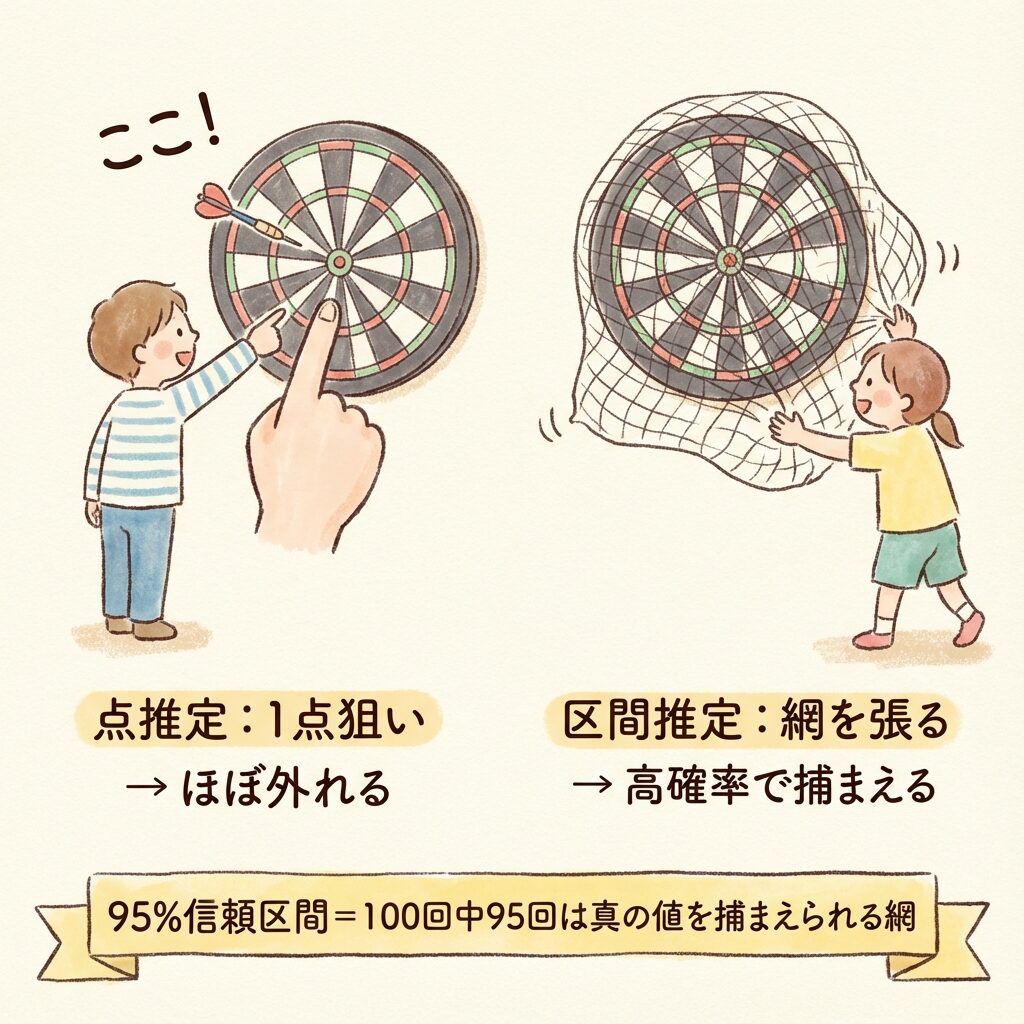
点推定:「的の中心はここだ!」と1点を指さす → ほぼ外れる
区間推定:「的の中心はこの範囲にある」と網を張る → 高確率で当たる
「95%信頼区間」なら、100回網を張ったら95回は真の値を捕まえられます。
| 推定方法 | 表現方法 | メリット |
|---|---|---|
| 点推定 | 「β = 5.0」 | シンプルでわかりやすい |
| 区間推定 | 「β は 2.39〜7.61 の範囲」 | 不確かさがわかる |
95%信頼区間の意味を正しく理解する
よくある誤解:「真の値がこの範囲にある確率が95%」ではない
「95%信頼区間」という言葉、直感的には「真の値βがこの範囲にある確率が95%」と思いがちですよね。
でも、これは厳密には正しくありません。
正しい解釈はこうです。
同じ方法でサンプリングと区間推定を100回繰り返したら、
そのうち95回は真の値βを含む区間が得られる。
つまり、「この1回の区間」が真の値を含んでいるかどうかは、実は「含んでいる」か「含んでいない」かの二択なんです。確率95%で揺らいでいるわけではありません。
…とはいえ、日常的には「真の値がこの範囲にある確率が高い」くらいの理解でOKです。
「95%信頼区間が 2.39〜7.61」とは…
「真の偏回帰係数βは、おそらく 2.39〜7.61 のどこかにある。
ただし、5%の確率で外れている可能性もある」
このくらいの理解で、ビジネス判断には十分使えます。
信頼水準を変えると何が変わる?
信頼区間は「95%」だけでなく、「90%」や「99%」で計算することもあります。
信頼水準を変えると、区間の幅が変わります。
| 信頼水準 | 区間の幅 | イメージ |
|---|---|---|
| 90% | 狭い | 小さい網 → 外れやすいが、当たれば精度高い |
| 95% | 中くらい | バランス型(最もよく使われる) |
| 99% | 広い | 大きい網 → 当たりやすいが、精度は粗い |
「確実に当てたい」なら99%、「精度を高めたい」なら90%…ですが、通常は95%がスタンダードです。特に理由がなければ95%を使いましょう。
信頼区間の計算式
公式:点推定値 ± t × 標準誤差
偏回帰係数の信頼区間は、次の公式で計算します。
bⱼ:偏回帰係数の点推定値
SE(bⱼ):偏回帰係数の標準誤差
t(φ, α/2):自由度φ、有意水準α/2のt分布の臨界値
βⱼ:真の偏回帰係数(推定したい値)
シンプルに言うと、こういうことです。
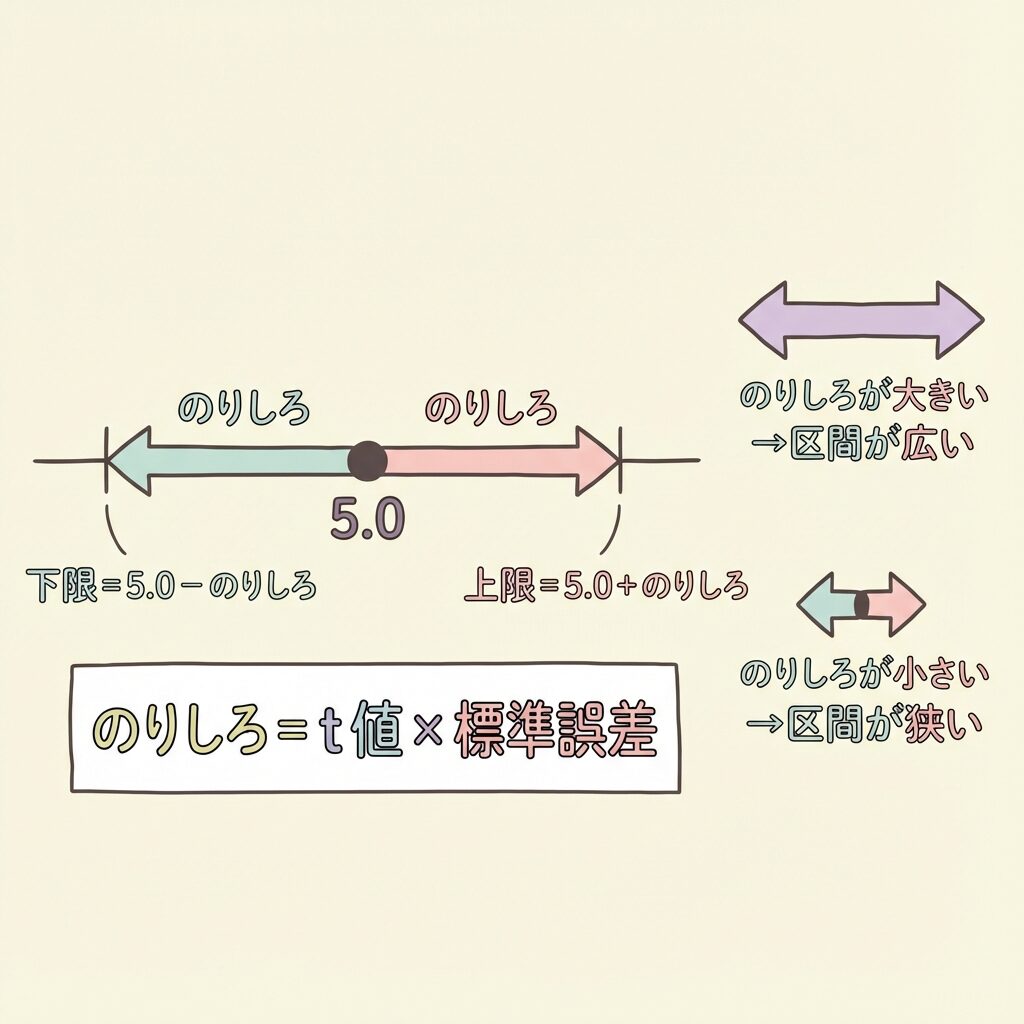
信頼区間 = 点推定値 ± 「のりしろ」
「のりしろ」= t値 × 標準誤差
点推定値を中心に、上下に「のりしろ」分だけ広げた範囲が信頼区間です。
「のりしろ」を決める2つの要素
「のりしろ」(= t値 × 標準誤差)の大きさは、2つの要素で決まります。
| 要素 | 大きいと… | 小さいと… |
|---|---|---|
| t値 (信頼水準で決まる) |
信頼水準が高い(99%など) → 区間が広がる |
信頼水準が低い(90%など) → 区間が狭まる |
| 標準誤差 (データの質で決まる) |
推定の不確かさが大きい → 区間が広がる |
推定の不確かさが小さい → 区間が狭まる |
区間を狭くしたい(精度を上げたい)なら、サンプルサイズを増やすのが王道です。サンプルが増えると標準誤差が小さくなり、区間が狭くなります。
【計算例】95%信頼区間を実際に求めてみよう
問題設定:売上を予測するモデル(前回の続き)
これまでと同じ例を使います。売上(y)を「広告費(x₁)」と「店舗面積(x₂)」で予測するモデルです。
- サンプルサイズ:n = 15
- 説明変数の数:k = 2
- 残差の自由度:φ = n − k − 1 = 12
| 変数 | 偏回帰係数 bⱼ | 標準誤差 SE(bⱼ) | t検定の結果 |
|---|---|---|---|
| 広告費 x₁ | 5.0 | 1.2 | 有意 ✓ |
| 店舗面積 x₂ | 2.0 | 1.5 | 有意でない ✗ |
この情報から、各変数の95%信頼区間を計算していきます。
ステップ1:t分布表からt値を求める
まず、95%信頼区間に必要なt値を求めます。
t分布表は、次の2つの情報で引きます。
t(12, 0.025) = 2.179
これが「のりしろ」を決めるt値です。
ステップ2:広告費(x₁)の信頼区間を計算
広告費の95%信頼区間を計算しましょう。
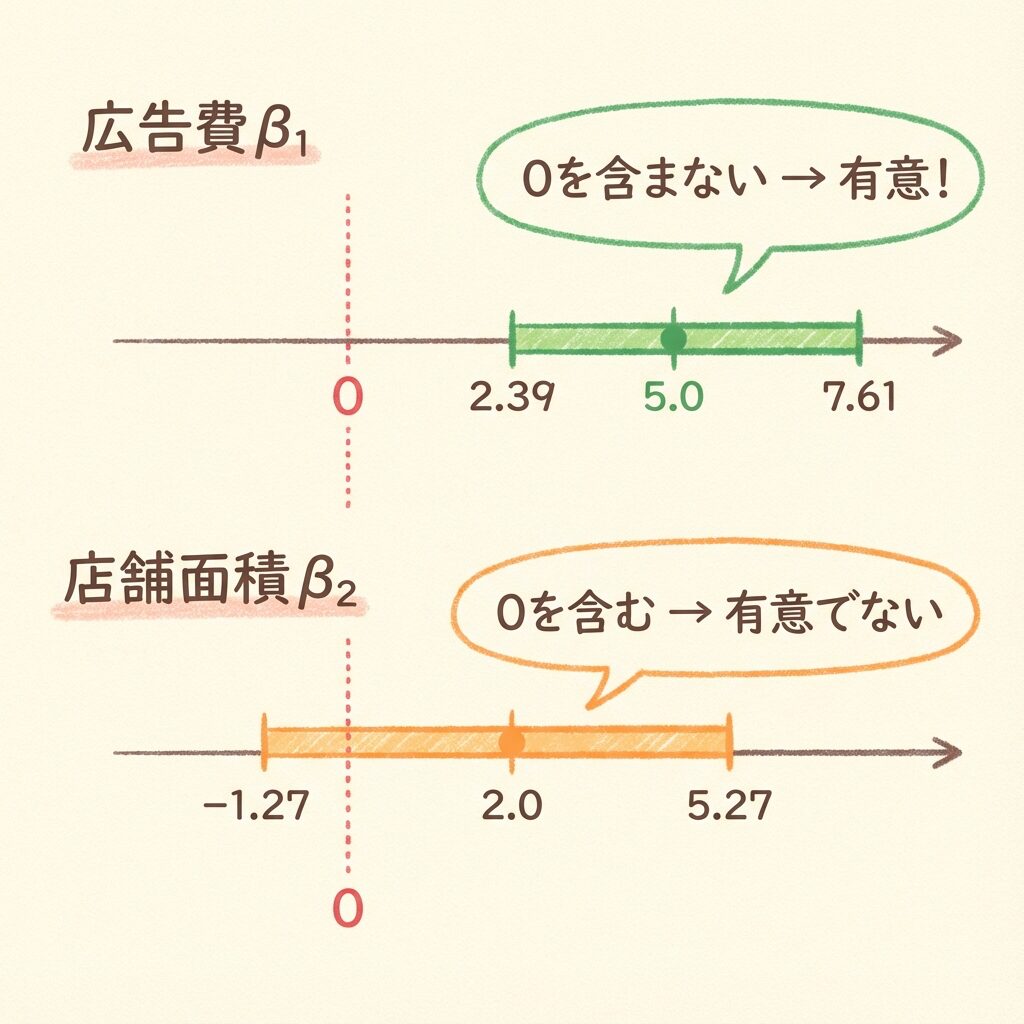
2.39 ≦ β₁ ≦ 7.61
これは何を意味するでしょうか?
「広告費を1万円増やすと、売上は2.39万円〜7.61万円増える」
点推定では「5万円増える」でしたが、区間推定では「2.39〜7.61万円のどこか」と幅を持たせています。
この方が現実的で、意思決定に使いやすいですよね。
ステップ3:店舗面積(x₂)の信頼区間を計算
同様に、店舗面積の95%信頼区間を計算します。
−1.27 ≦ β₂ ≦ 5.27
ここで重要なポイントに気づきましたか?
店舗面積の信頼区間は「0」を含んでいます(−1.27〜5.27)。
これは何を意味するでしょうか?
信頼区間から「有意性」も判定できる
裏技:信頼区間が「0」を含むかどうかでt検定と同じ判定ができる
実は、信頼区間を見るだけでt検定と同じ判定ができます。
信頼区間が0を含まない → 有意(その変数は効いている)
信頼区間が0を含む → 有意でない(効いているとは言えない)
なぜこれでわかるのでしょうか?
帰無仮説は「βⱼ = 0(この変数は効いていない)」でしたよね。
信頼区間が0を含まないということは、「真の値βⱼが0である可能性は95%の確率で否定される」ということ。つまり、帰無仮説を棄却できるのです。
今回の例で確認してみよう
| 変数 | 95%信頼区間 | 0を含む? | 判定 |
|---|---|---|---|
| 広告費 x₁ | 2.39 〜 7.61 | 含まない | 有意 ✓ |
| 店舗面積 x₂ | −1.27 〜 5.27 | 含む | 有意でない ✗ |
前回のt検定の結果と完全に一致していますね。
t検定:「有意かどうか」だけがわかる(Yes/No)
区間推定:「有意かどうか」+「効果の大きさの範囲」がわかる
区間推定の方が情報量が多いので、両方報告するのがベストです。
99%信頼区間も計算してみよう
信頼水準を上げると区間はどう変わる?
参考として、99%信頼区間も計算してみましょう。
99%信頼区間に必要なt値は、α = 0.01 → α/2 = 0.005 で引きます。
t(12, 0.005) = 3.055
95%のときの t = 2.179 より大きくなっていますね。これで「のりしろ」が広がります。
広告費(x₁)の99%信頼区間
下限 = 5.0 − 3.67 = 1.33
上限 = 5.0 + 3.67 = 8.67
1.33 ≦ β₁ ≦ 8.67
店舗面積(x₂)の99%信頼区間
下限 = 2.0 − 4.58 = −2.58
上限 = 2.0 + 4.58 = 6.58
−2.58 ≦ β₂ ≦ 6.58
95%と99%の比較
| 変数 | 95%信頼区間 | 99%信頼区間 | 区間の幅 |
|---|---|---|---|
| 広告費 x₁ | 2.39 〜 7.61 (幅 5.22) |
1.33 〜 8.67 (幅 7.34) |
広がった |
| 店舗面積 x₂ | −1.27 〜 5.27 (幅 6.54) |
−2.58 〜 6.58 (幅 9.16) |
広がった |
信頼水準を95%から99%に上げると、区間の幅が約1.4倍に広がりました。
「確実に当てたい」なら99%ですが、その分「精度」は落ちます。このトレードオフを理解して、目的に応じて使い分けましょう。

信頼区間を狭くするには?
サンプルサイズを増やすのが王道
「信頼区間が広すぎて、意思決定に使えない…」
そんなときは、サンプルサイズを増やすのが最も効果的です。
サンプルサイズnが増えると、次の2つの効果があります。
| 効果 | 理由 |
|---|---|
| 標準誤差が小さくなる | データが増えると推定の精度が上がるため |
| t値が小さくなる | 自由度が増えるとt分布が正規分布に近づくため |
「のりしろ = t値 × 標準誤差」なので、両方が小さくなれば区間は確実に狭くなります。
サンプルサイズを4倍にすると、標準誤差は約半分になります。
(標準誤差は √n に反比例するため)
例:n = 15 → n = 60 にすると、区間の幅がおよそ半分に。
その他の方法
- 信頼水準を下げる(99% → 95% → 90%):ただしリスクは増える
- 測定精度を上げる:データのバラつきを減らす
- 説明変数を増やす:残差の分散が減れば標準誤差も減る(ただし多重共線性に注意)
計算手順のまとめ
- t値を求める:t分布表から t(φ, α/2) を引く
- 「のりしろ」を計算:のりしろ = t値 × 標準誤差
- 下限を計算:下限 = 点推定値 − のりしろ
- 上限を計算:上限 = 点推定値 + のりしろ
- 0を含むかチェック:含まなければ有意
まとめ
この記事では、偏回帰係数の区間推定について解説しました。
- 点推定は1点で推定、区間推定は幅で推定
- 信頼区間 = 点推定値 ± t値 × 標準誤差
- 95%信頼区間が最もよく使われる
- 信頼区間が0を含まない → 有意と判定できる
- 区間を狭くするにはサンプルサイズを増やすのが王道
区間推定をマスターしたら、次は「重回帰分析がうまくいかない原因」として有名な多重共線性(VIF)について学びましょう。
📚 次に読むべき記事
説明変数同士が相関していると何が起こるのか?
t検定の計算方法を復習したい方へ
区間推定の基礎から学びたい方へ