📝 こんな悩みはありませんか?
- 😕「ウィルコクソン検定」って名前は聞くけど、結局なにをする検定?
- 🤔t検定との違いがよくわからない…どっちを使えばいいの?
- 💭「順位」で比較するってどういうこと?イメージがわかない…
✨ この記事の結論
ウィルコクソン検定は「データを順位に変換して比較する」検定です。
正規分布を仮定しない「ノンパラメトリック検定」の代表格。
サンプルが少ないとき、外れ値があるときに威力を発揮します!
「このダイエット法、本当に効果あったのかな?」
「AグループとBグループ、どっちの成績がいいんだろう?」
こんなとき、統計的に比較したいですよね。
比較の検定といえば「t検定」が有名です。でも、t検定には「データが正規分布に従っていること」という前提条件があります。
では、正規分布に従わないデータはどうすればいいのでしょうか?
サンプル数が少なくて、正規分布かどうかもわからないときは?
そんなときに活躍するのが、「ウィルコクソンの順位検定」です。
この記事では、ウィルコクソン検定の考え方・種類・使いどころを、マラソンの順位などの身近な例を使って、初心者の方でも「なるほど!」とイメージできるように解説していきますね。
目次
🏅 ウィルコクソン検定とは?|「順位」で比較する検定
まずは「ウィルコクソン検定ってそもそも何?」というところから、やさしく説明していきます。
🔢 数値を「順位」に変換するのがポイント
ウィルコクソン検定の最大の特徴は、「データの数値そのものではなく、順位を使って比較する」ことです。
たとえば、マラソン大会を想像してみてください。
🏃 マラソンで例えると…
5人のランナーのゴールタイム:
Aさん:3時間10分、Bさん:2時間55分、Cさん:4時間20分、Dさん:3時間05分、Eさん:3時間30分
これを順位に変換すると:
Aさん:3位、Bさん:1位、Cさん:5位、Dさん:2位、Eさん:4位
タイムの「数値」ではなく「順位」で比較するのがウィルコクソン検定の考え方です。
「え、なんでわざわざ順位に変えるの?数値のまま比較した方が正確じゃない?」と思いますよね。実は、順位に変換することで大きなメリットがあるんです。
💪 順位に変換するメリット
順位に変換する最大のメリットは、「外れ値の影響を受けにくい」ことです。
😰 数値のまま比較すると…
データ:10, 12, 15, 11, 200(外れ値)
平均:49.6(外れ値に引っ張られる!)
→ 実態とかけ離れた結果に…
😊 順位に変換すると…
順位:2位, 3位, 4位, 1位, 5位
→ 外れ値も「5位」として扱われるだけ
→ 影響が小さくなる!
つまり、極端な値があっても、それはただの「最下位」や「最上位」として扱われるだけなので、全体の結果を大きく歪めないんですね。
💡 ノンパラメトリック検定とは?
ウィルコクソン検定は「ノンパラメトリック検定」の一種です。
「ノンパラメトリック」=「母集団の分布を仮定しない」という意味。
正規分布じゃなくても使えるので、幅広い場面で活躍します。
⚖️ t検定との違い
「比較の検定」といえばt検定が有名ですよね。ウィルコクソン検定とt検定、何が違うのでしょうか?
📊 t検定 vs ウィルコクソン検定
| t検定 | ウィルコクソン検定 | |
|---|---|---|
| 分布の仮定 | 正規分布が必要 | 不要(ノンパラメトリック) |
| 比較するもの | 平均値 | 順位(中央値の傾向) |
| 外れ値への強さ | 弱い(影響を受けやすい) | 強い(影響を受けにくい) |
| サンプルサイズ | ある程度必要(目安:30以上) | 小さくてもOK |
| 検出力 | 高い(条件を満たせば) | やや低い |
簡単に言うと、「条件が整っていればt検定の方が優秀」だけど、「条件が整っていなくても使えるのがウィルコクソン検定」ということですね。

🎯 2種類のウィルコクソン検定|対応あり?なし?
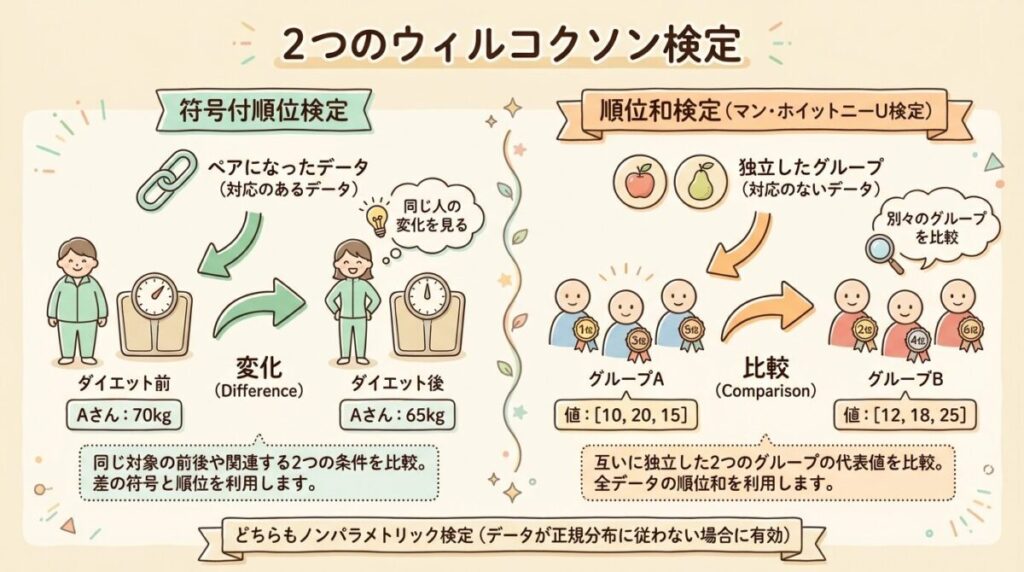
実は、「ウィルコクソン検定」と呼ばれるものには2種類あります。
「データに対応があるかどうか」で使い分けるんですね。ここが混乱しやすいポイントなので、しっかり整理しておきましょう。
①符号付順位検定
Wilcoxon Signed-Rank Test
「対応あり」のデータ用
同じ対象の「前」と「後」を比較
例:同じ人のダイエット前後の体重
対応のあるt検定の
ノンパラメトリック版
②順位和検定
Wilcoxon Rank-Sum Test(= Mann-Whitney U検定)
「対応なし」のデータ用
別々のグループを比較
例:A組とB組のテスト成績
対応のないt検定の
ノンパラメトリック版
🤔 「対応あり」「対応なし」ってどういうこと?
✅ 対応あり(ペアがある)
- 同じ人の「前」と「後」
- 同じ製品の「処理A」と「処理B」
- 夫婦や双子のペアデータ
→ 1対1で対応づけられるデータ
✅ 対応なし(独立している)
- A組の生徒 vs B組の生徒
- 男性グループ vs 女性グループ
- 新薬投与群 vs プラセボ群
→ 別々の集団を比較するデータ
📌 使い分けフローチャート
「どっちを使えばいいの?」と迷ったら、このフローチャートで確認しましょう。
YES(同じ対象の前後など)
↓(Wilcoxon Signed-Rank)
NO(別々のグループ)
↓(Mann-Whitney U)
⚠️ 名前の混乱に注意!
「順位和検定」は「マン・ホイットニーのU検定」とも呼ばれます。
実は数学的には同じ検定なんです。文献によって呼び方が違うので、混乱しないように注意しましょう。
📝 符号付順位検定のやり方|5ステップで完全理解
では、「符号付順位検定」の具体的な手順を見ていきましょう。
ダイエットプログラムの効果を検証する例で、ステップバイステップで解説しますね。
📊 例題:ダイエットプログラムの効果検証
6人がダイエットプログラムに参加しました。
「プログラム前後で体重に有意な差があるか?」を検定します。
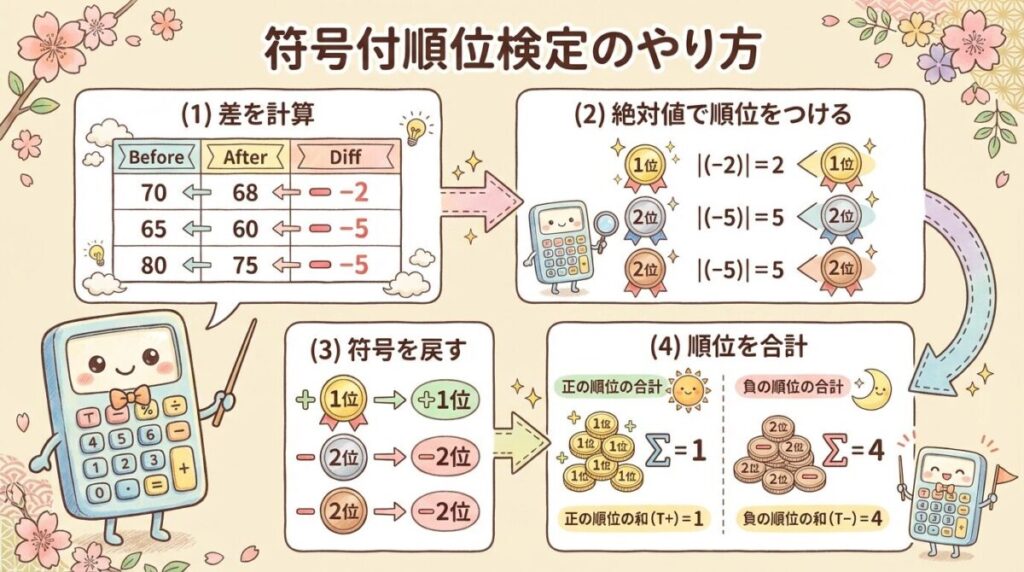
Step 1:差を計算する
まず、各参加者の「後 − 前」の差を計算します。
| 参加者 | 差(後−前) | 符号 |
|---|---|---|
| Aさん | 68 − 70 = −2 | − |
| Bさん | 64 − 65 = −1 | − |
| Cさん | 75 − 80 = −5 | − |
| Dさん | 70 − 72 = −2 | − |
| Eさん | 69 − 68 = +1 | + |
| Fさん | 71 − 75 = −4 | − |
マイナス(体重が減った)が5人、プラス(体重が増えた)が1人ですね。
Step 2:絶対値で順位をつける
次に、差の「絶対値」(プラスマイナスを無視した値)で順位をつけます。
| 参加者 | 差 | 絶対値 | 順位 |
|---|---|---|---|
| Bさん | −1 | 1 | 1.5 |
| Eさん | +1 | 1 | 1.5 |
| Aさん | −2 | 2 | 3.5 |
| Dさん | −2 | 2 | 3.5 |
| Fさん | −4 | 4 | 5 |
| Cさん | −5 | 5 | 6 |
💡 「タイ(同順位)」の処理
絶対値が同じ値(タイ)がある場合は、順位の平均をとります。
例:絶対値「1」が2つ → 1位と2位の平均で 1.5位
例:絶対値「2」が2つ → 3位と4位の平均で 3.5位
Step 3:符号を戻して、順位を合計する
順位に元の符号(+/−)を戻して、プラスの順位の合計(W+)とマイナスの順位の合計(W−)を計算します。
➕ プラスの順位和(W+)
Eさんのみ:W+ = 1.5
➖ マイナスの順位和(W−)
1.5 + 3.5 + 3.5 + 5 + 6 = W− = 19.5
Step 4:検定統計量を求める
検定統計量Wは、W+とW−の小さい方を使います。
W = min(W+, W−) = min(1.5, 19.5) = 1.5
Step 5:統計表と比較して判定
最後に、求めたWを「ウィルコクソン検定表」の臨界値と比較します。
n=6(差が0でないデータ数)、有意水準5%(両側)の場合、臨界値は0です。
判定基準:W ≦ 臨界値 なら「有意差あり」
今回:W = 1.5 > 臨界値 0
→ 有意水準5%では「有意差なし」と判定
ただし、サンプルサイズが6と非常に小さいため、検出力が低いことに注意が必要です。傾向としては体重が減っている人が多いので、サンプルを増やせば有意になる可能性があります。
📊 順位和検定(マン・ホイットニーU検定)のやり方
次に、「順位和検定」(マン・ホイットニーU検定)の手順を見ていきましょう。
こちらは「対応のない(独立した)2群」を比較する検定です。
📊 例題:2つのクラスのテスト成績比較
A組(4人)とB組(3人)のテスト成績を比較します。
「2つのクラスに成績の差があるか?」を検定します。
A組(n₁=4)
72, 85, 68, 90
B組(n₂=3)
65, 78, 70
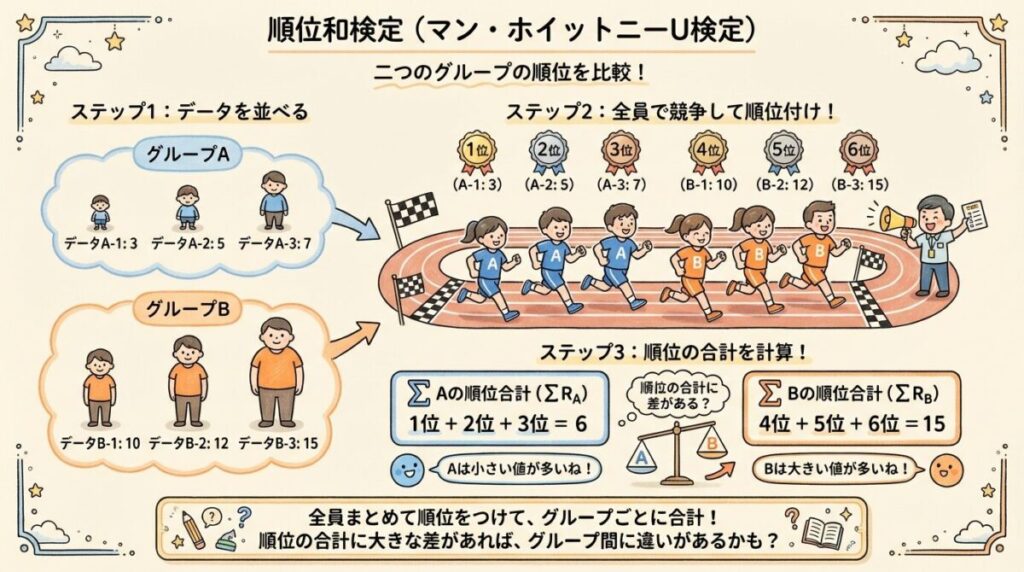
Step 1:全データをまとめて順位をつける
まず、A組とB組のデータを全部まとめて、小さい順に順位をつけます。
| 点数 | 所属 | 順位 |
|---|---|---|
| 65 | B組 | 1 |
| 68 | A組 | 2 |
| 70 | B組 | 3 |
| 72 | A組 | 4 |
| 78 | B組 | 5 |
| 85 | A組 | 6 |
| 90 | A組 | 7 |
Step 2:各グループの順位和を計算
グループごとに順位を合計します。
A組の順位和(R₁)
2 + 4 + 6 + 7 = 19
B組の順位和(R₂)
1 + 3 + 5 = 9
検算:R₁ + R₂ = 19 + 9 = 28 = 7×8÷2 = n(n+1)/2 ✓
Step 3:U統計量を計算
マン・ホイットニーのU統計量を計算します。
計算式:U₁ = n₁×n₂ + n₁(n₁+1)/2 − R₁
U₁ = 4×3 + 4×5/2 − 19 = 12 + 10 − 19 = 3
U₂ = 4×3 + 3×4/2 − 9 = 12 + 6 − 9 = 9
U = min(U₁, U₂) = min(3, 9) = 3
Step 4:統計表と比較して判定
n₁=4、n₂=3、有意水準5%(両側)の場合、臨界値は0です。
判定基準:U ≦ 臨界値 なら「有意差あり」
今回:U = 3 > 臨界値 0
→ 有意水準5%では「有意差なし」と判定
A組の方が成績上位に位置していますが、サンプルサイズが小さいため、統計的に有意とは言えませんでした。実務では、もっと多くのサンプルで検証することが重要です。
📝 まとめ|ウィルコクソン検定を使いこなそう
最後に、この記事のポイントをまとめます。
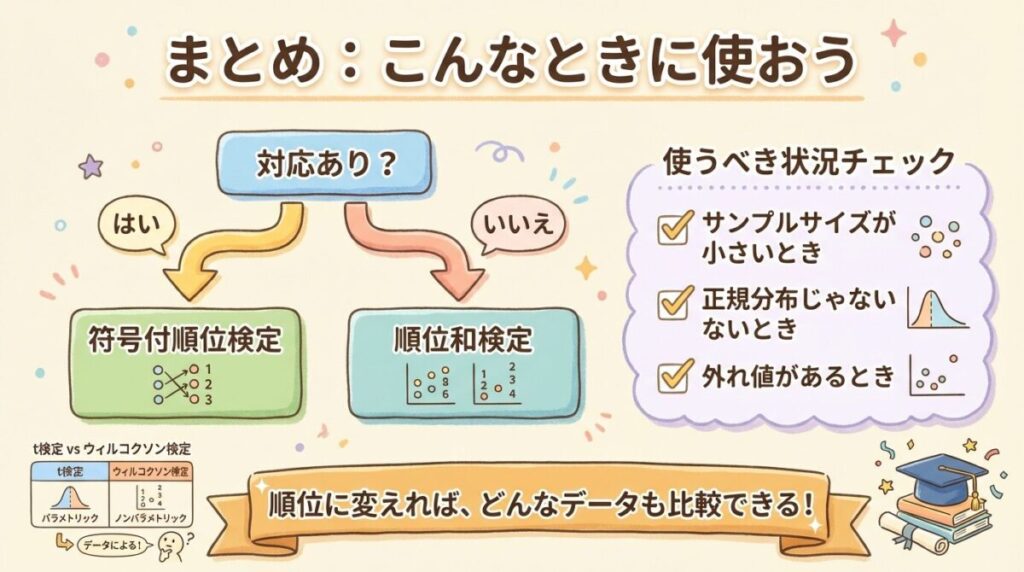
✅ この記事のまとめ
1. ウィルコクソン検定とは:データを「順位」に変換して比較するノンパラメトリック検定。正規分布を仮定しなくてOK。
2. 2種類の検定:「対応あり」なら符号付順位検定、「対応なし」なら順位和検定(マン・ホイットニーU検定)を使う。
3. メリット:外れ値に強い、サンプルサイズが小さくても使える、分布の形を気にしなくていい。
4. 使いどころ:正規分布じゃないとき、サンプルが少ないとき、順序尺度データのとき。
🎯 検定の使い分け早見表
| 状況 | 対応あり | 対応なし |
|---|---|---|
| 正規分布OK・大サンプル | 対応のあるt検定 | 対応のないt検定 |
| 正規分布NG・小サンプル | 符号付順位検定 | 順位和検定(U検定) |
ウィルコクソン検定は、「t検定が使えないとき」の強力な代替手段です。特に実務では、データが正規分布に従わないケースが多いので、ぜひ使いこなせるようになっておきましょう。
QC検定でもノンパラメトリック検定は出題されますので、しっかり理解しておいてくださいね。
📚 次に読むべき記事