- 「分散の加法性って何?なんで分散は足せるの?」
- 「標準偏差は足せないのに、分散は足せる?意味がわからない…」
- 「『独立』ってどういう意味?」
- 「V(X+Y) = V(X) + V(Y) の公式、どう使えばいいの?」
統計学で必ず登場する「分散の加法性」。QC検定や統計検定でも頻出の超重要テーマです。
でも、「なぜ分散は足せるのか」「どんな条件で使えるのか」が曖昧なまま公式を暗記していませんか?
この記事では、サイコロ2個の例を使って、分散の加法性を徹底的に図解します。読み終わる頃には「なるほど、そういうことか!」とスッキリするはずです。
- 独立な確率変数なら、分散は足し算できる
- V(X + Y) = V(X) + V(Y) ← これが「分散の加法性」
- 標準偏差は足せない(2乗してから足して、ルートを取る)
- 引き算でもV(X − Y) = V(X) + V(Y)(プラスになる!)
目次
🎲 サイコロ2個で考えよう
分散の加法性を理解するために、サイコロを2個振るケースを考えましょう。
サイコロ1個の出目をX、もう1個の出目をYとします。
2個の合計はX + Yですね。
🎯 サイコロ1個の統計量
まず、サイコロ1個の期待値と分散を確認しましょう。
| 出目 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 確率 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
では、サイコロを2個振ったとき、合計X + Yの分散はどうなるでしょうか?

🔗 「独立」とは?分散の加法性の条件
分散の加法性が成り立つには、「独立」という条件が必要です。
「独立」とは、一方の結果がもう一方に影響しないことを意味します。
サイコロXで「6」が出たからといって、サイコロYの出目は変わりませんよね。
Xの結果とYの結果はお互いに影響しない。
これが「独立」です。
✅ 独立の例
| 独立な例 ✅ | 独立でない例 ❌ |
|---|---|
| サイコロ2個を振る | 身長と体重(相関がある) |
| コイン2枚を投げる | 気温とアイスの売上 |
| 工程Aと工程Bの誤差(別機械) | 同じ機械の連続測定 |
➕ 分散の加法性の公式
XとYが独立なら、以下の公式が成り立ちます。
V(X + Y) = V(X) + V(Y)
※ XとYが独立の場合に限る
サイコロ2個の合計の分散を計算してみましょう。
V(X + Y) = V(X) + V(Y) = 2.92 + 2.92 = 5.84
はい、分散は単純に足せます!これが分散の加法性です。
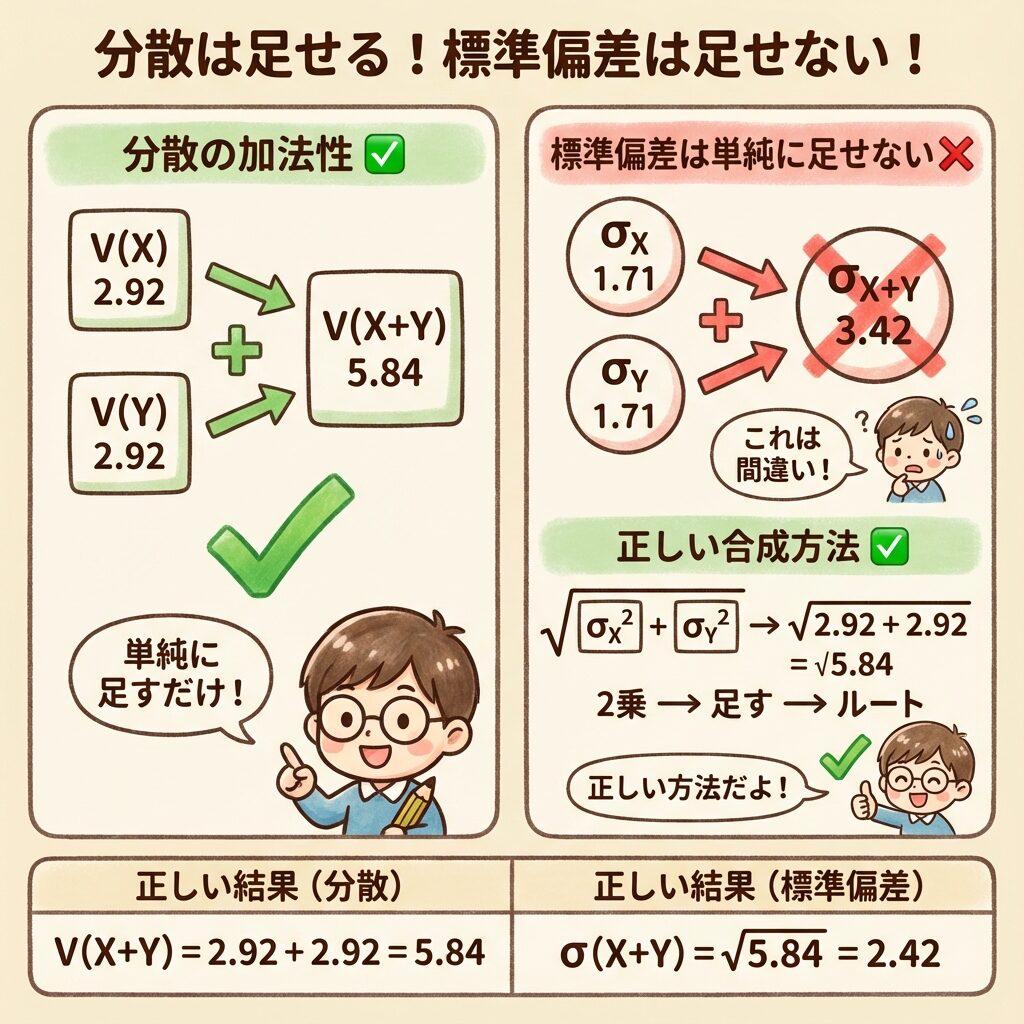
⚠️ 注意!標準偏差は足せない
ここで重要な注意点があります。標準偏差は単純に足せません。
| 計算 | 正しい? | 結果 |
|---|---|---|
| σX + σY = 1.71 + 1.71 | ❌ 間違い | 3.42 |
| √(V(X) + V(Y)) = √5.84 | ✅ 正しい | 2.42 |
標準偏差を合成するには、2乗→足す→ルートの3ステップ!
σX+Y = √(σX² + σY²) = √(V(X) + V(Y))
➖ 引き算でも分散は「足す」!
ここで、多くの人が間違えるポイントがあります。
X − Yの分散はどうなるでしょうか?「引き算だから分散も引く」と思いがちですが…
V(X − Y) = V(X) + V(Y)
※ マイナスではなくプラス!
なぜプラスになるのでしょうか?
🤔 なぜ引き算でもプラス?
分散は「バラつき」を表す量です。バラつきに「マイナス」はありません。
AさんとBさんがそれぞれ的を狙って投げます。
二人の差を考えるとき、バラつきは増えるんです。
なぜなら、Aさんがズレて、Bさんもズレると、
差のバラつきは両方のズレが重なるから!
数学的には、V(−Y) = V(Y) となります。マイナスの符号は分散には影響しないんです。
V(X − Y) = V(X + (−Y)) = V(X) + V(−Y) = V(X) + V(Y)
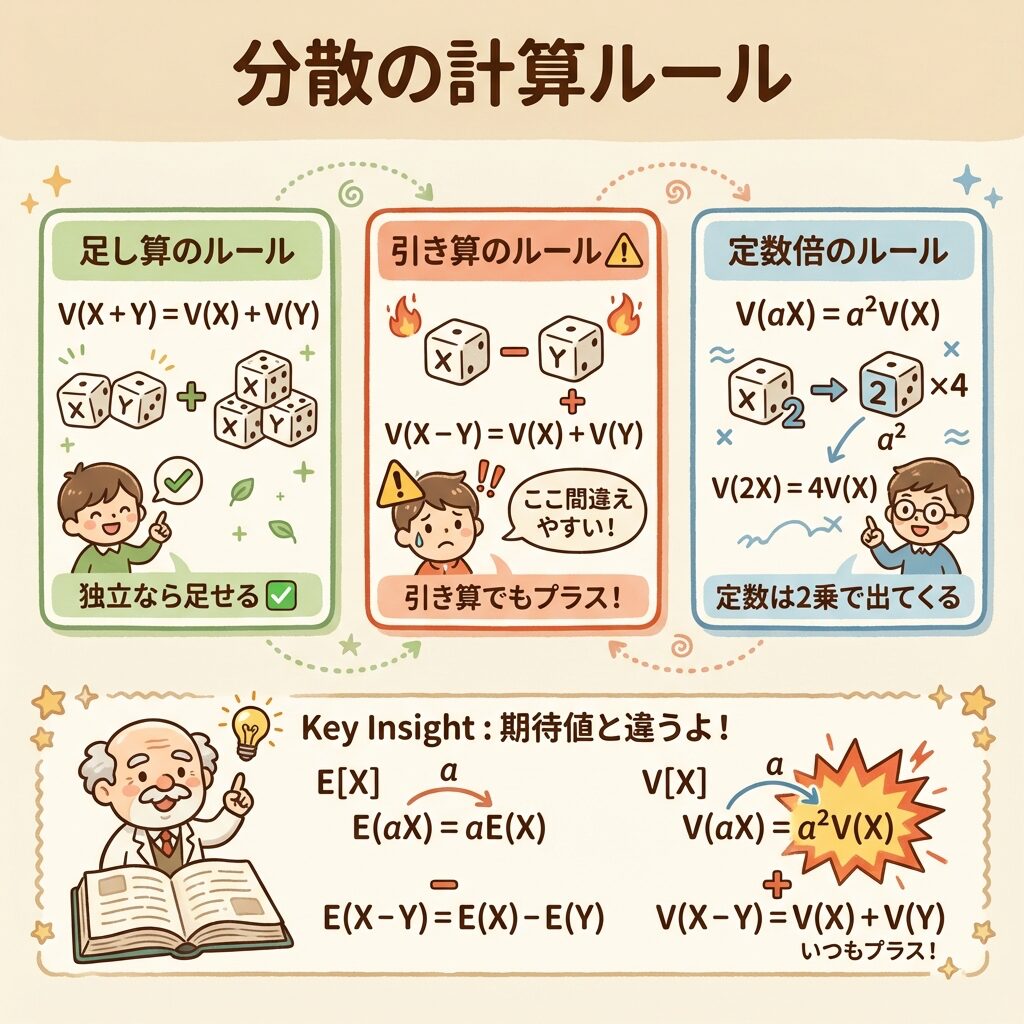
✖️ 定数倍の分散
もう一つ重要な公式があります。確率変数を定数倍したときの分散です。
V(aX) = a²V(X)
定数は「2乗」されて出てくる
例えば、Xを2倍したら、分散は4倍になります。
V(2X) = 2² × V(X) = 4V(X)
📋 分散の公式まとめ
| 公式 | 条件 | ポイント |
|---|---|---|
| V(X + Y) = V(X) + V(Y) | X, Y が独立 | 分散は足せる |
| V(X − Y) = V(X) + V(Y) | X, Y が独立 | 引き算でもプラス! |
| V(aX) = a²V(X) | aは定数 | 定数は2乗で出る |
| V(X + a) = V(X) | aは定数 | 定数を足しても分散は変わらない |
🏭 実務での活用例|製造業の品質管理
分散の加法性は、製造業の品質管理で大活躍します。
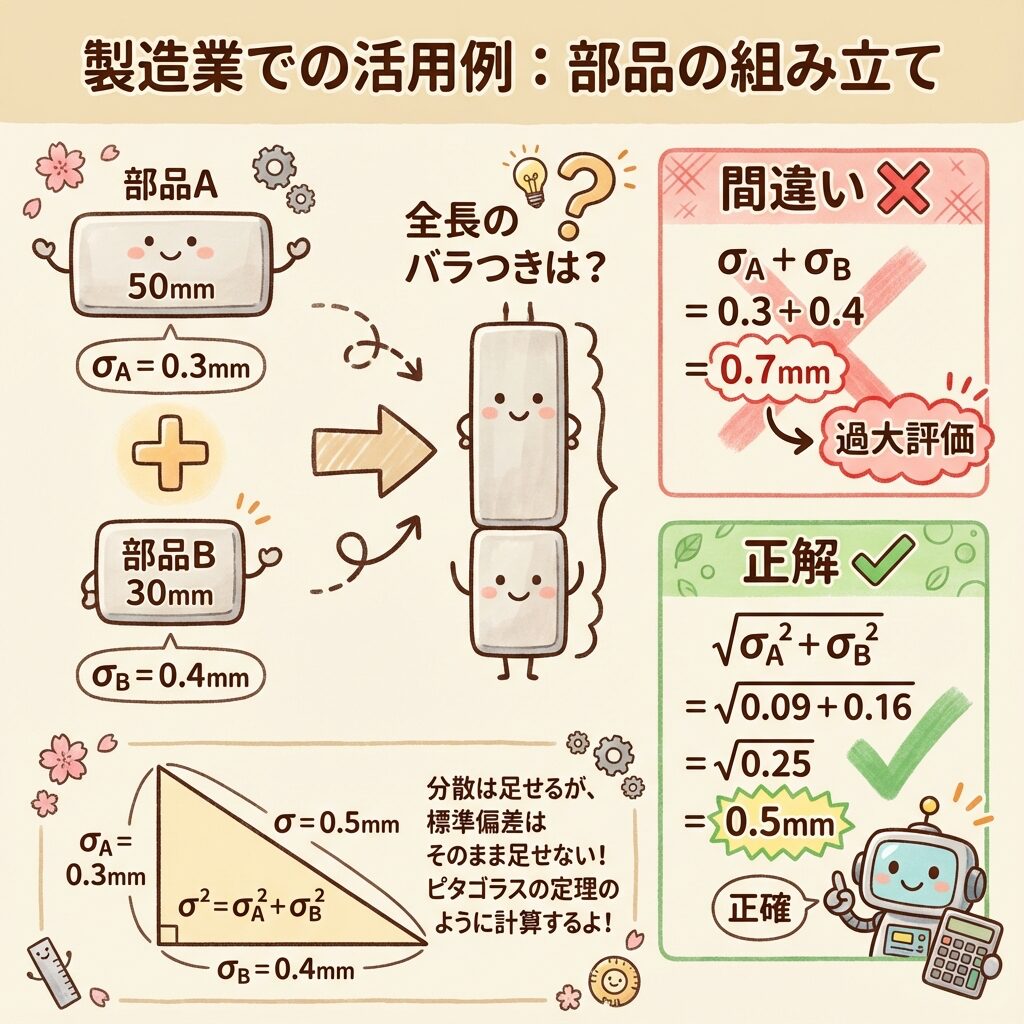
🔧 例題:部品の組み立て
部品Aと部品Bを組み合わせて製品を作ります。それぞれの寸法のバラつきは以下の通りです。
| 部品 | 目標寸法 | 標準偏差 σ | 分散 σ² |
|---|---|---|---|
| 部品A | 50mm | 0.3mm | 0.09mm² |
| 部品B | 30mm | 0.4mm | 0.16mm² |
問題:組み立て後の全長(A + B)のバラつき(標準偏差)はいくらになる?
📝 解答
Step 1:分散を足す
V(A + B) = V(A) + V(B) = 0.09 + 0.16 = 0.25mm²
Step 2:平方根を取って標準偏差へ
σA+B = √0.25 = 0.5mm
間違い:0.3 + 0.4 = 0.7mm(標準偏差を直接足す)
正解:√(0.3² + 0.4²) = √0.25 = 0.5mm
標準偏差を直接足すと、バラつきを過大評価してしまいます!
💡 なぜ直接足すと大きくなる?
部品AとBが同時に最大にズレる確率は低いですよね。
Aが大きくズレているとき、Bは小さいかもしれない。逆もあり得る。
だから、単純に足し合わせるよりも、実際のバラつきは小さくなるんです。
分散の加法性は、ピタゴラスの定理に似ています。
直角三角形で、斜辺c = √(a² + b²) ですよね。
3² + 4² = 9 + 16 = 25 → √25 = 5
標準偏差の合成も同じ!
σ² + σ² を足して √ を取るイメージです。
📚 まとめ|分散の加法性の要点
- 独立な確率変数なら、分散は足し算できる
- 標準偏差は足せない(2乗→足す→ルートの3ステップ)
- 引き算でもV(X−Y) = V(X) + V(Y)(プラスになる!)
- 定数倍はV(aX) = a²V(X)(2乗で出てくる)
- 製造業の公差計算で必須の知識
| V(X + Y) = V(X) + V(Y) | 独立なら足せる |
| V(X − Y) = V(X) + V(Y) | 引き算でもプラス! |
| V(aX) = a²V(X) | 定数は2乗で出る |
| V(X + a) = V(X) | 定数を足しても分散は不変 |
- V(X − Y)がプラスになる理由を説明できるように
- 標準偏差の合成方法「2乗→足す→ルート」を暗記
- 「独立」の条件を確認する問題に注意
- 公差計算への応用問題が頻出
- 標準偏差を直接足す(σX + σY は間違い!)
- V(X − Y) = V(X) − V(Y) と計算する(マイナスではない!)
- 独立でない変数に加法性を適用する
📖 統計学基礎シリーズ
第5回:分散と標準偏差 - ばらつきを数値化する →
【完全版】統計学の勉強ロードマップ →
分散の加法性は「独立ならバラつきは足せる」という法則でしたね。
標準偏差は直接足せないけど、「2乗→足す→ルート」で合成できます。
引き算でもプラスになるのがポイント!
次は「共分散」で、独立でない場合を学びましょう!➕📊
統計学のおすすめ書籍
統計学の「数式アレルギー」を治してくれた一冊
「Σ(シグマ)や ∫(インテグラル)を見ただけで眠くなる…」 そんな私を救ってくれたのが、小島寛之先生の『完全独習 統計学入門』です。
この本は、難しい記号を一切使いません。 「中学レベルの数学」と「日本語」だけで、検定や推定の本質を驚くほど分かりやすく解説してくれます。
「計算はソフトに任せるけど、統計の『こころ(意味)』だけはちゃんと理解したい」 そう願う学生やエンジニアにとって、これ以上の入門書はありません。
【QC2級】「どこが出るか」がひと目で分かる!最短合格へのバイブル
私がQC検定2級に合格した際、使い倒したのがこの一冊です。
この本の最大の特徴は、「各単元の平均配点(何点分出るか)」が明記されていること。 「ここは出るから集中」「ここは出ないから流す」という戦略が立てやすく、最短ルートで合格ラインを突破できます。
解説が分かりやすいため、私はさらに上の「QC1級」を受験する際にも、基礎の確認用として辞書代わりに使っていました。 迷ったらまずはこれを選んでおけば間違いありません。