🎯 この記事でわかること
✅ 共分散とは「2つのデータの仲良し度」を測る道具
✅ 正・負・ゼロの3パターンをシーソーで理解
✅ なぜ共分散だけでは不十分なのか?(相関係数への伏線)
✅ 「相関≠因果」の落とし穴を回避する方法
目次
はじめに|「一緒に動く」関係を数値化したい
私たちの周りには、「2つのものが一緒に変化する現象」がたくさんあります。
☀️ 気温が上がると、アイスクリームの売上も上がる
📚 勉強時間が増えると、テストの点数も上がる
🌧️ 雨の日が多いと、傘の売上も増える
🍺 気温が上がると、ビールの消費量も増える
こういった「一緒に動く関係」を、感覚ではなく「数値」で表す道具——それが共分散(きょうぶんさん)です。
今回は、難しい数式を使わずに、「2人の友達の仲良し度」に例えて共分散を理解していきましょう。
共分散の正体|「2人が一緒に動くかどうか」を測る
🎭 たとえ話:2人の友達の「仲良し度」
あなたには、AさんとBさんという2人の友達がいます。
毎日2人の「テンション」を観察してみたところ、こんなパターンがあることに気づきました。
パターン①:Aさんがハイテンションの日は、Bさんもハイテンション
「2人とも同じ方向に動く」
→ これが正の共分散(仲良し!)
パターン②:Aさんがハイテンションの日は、Bさんはローテンション
「2人が逆方向に動く」
→ これが負の共分散(シーソーの関係!)
パターン③:Aさんのテンションに関係なく、Bさんは自由
「2人に関連がない」
→ これが共分散≒0(無関係!)
共分散とは、「2つのデータがどれくらい一緒に動くか」を数値化したものです。
正の共分散(+):一緒に上がる・一緒に下がる
負の共分散(−):一方が上がると、もう一方は下がる
共分散≒0:お互いに無関係

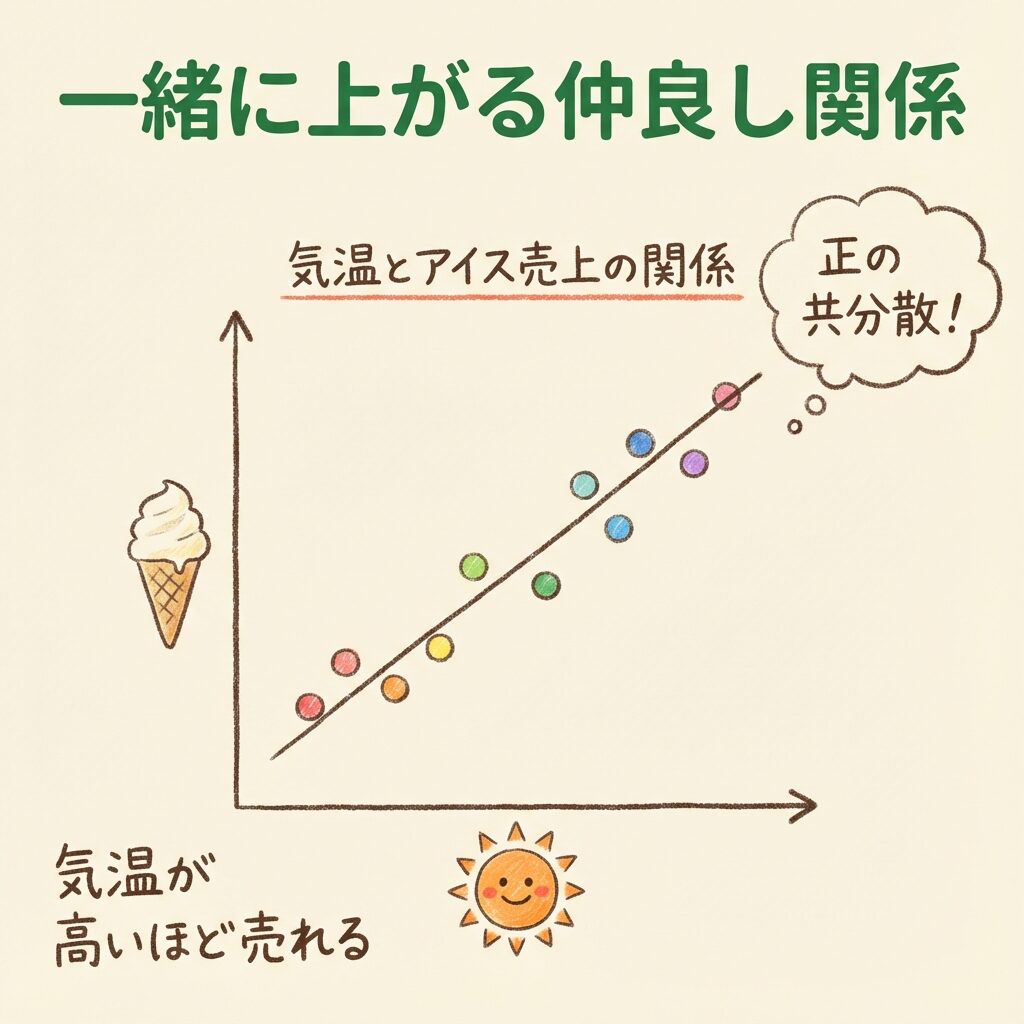
具体例①|気温とアイスクリーム売上の関係
コンビニで1週間、気温とアイスクリームの売上を調べました。
| 曜日 | 気温(℃) | アイス売上(個) |
|---|---|---|
| 月 | 18 | 120 |
| 火 | 22 | 180 |
| 水 | 25 | 220 |
| 木 | 28 | 280 |
| 金 | 32 | 350 |
| 土 | 35 | 420 |
| 日 | 30 | 320 |
表を見ると、「気温が高い日ほど、アイスがたくさん売れている」ことがわかりますね。
これを散布図にすると、こうなります。
アイス売上(個) 450| ★(土曜:35℃、420個) 400| 350| ●(金曜) 300| ●(日曜) 250| ●(木曜) 200| ●(水曜) 150| ●(火曜) 100|●(月曜) +------------------------ 15 20 25 30 35 気温(℃)
右肩上がりの直線になっていますね!これが「正の共分散」の典型例です。
🧮 共分散の計算イメージ
共分散は、次のような発想で計算します。
🔍 共分散の計算ステップ
① 気温の「平均からのズレ」を計算する
② 売上の「平均からのズレ」を計算する
③ 両方のズレをかけ算する
④ その合計を平均する → これが共分散!
なぜ「かけ算」するのか?
これがポイントです。
| 気温のズレ | 売上のズレ | かけ算の結果 | 意味 |
|---|---|---|---|
| +(平均より高い) | +(平均より多い) | + | 一緒に上がってる! |
| −(平均より低い) | −(平均より少ない) | + | 一緒に下がってる! |
| +(平均より高い) | −(平均より少ない) | − | 逆方向に動いてる! |
つまり、「同じ方向に動く」とプラス、「逆方向に動く」とマイナスになる仕組みです!
第5回:分散と標準偏差|「バラつき」を数値化する魔法の公式 →
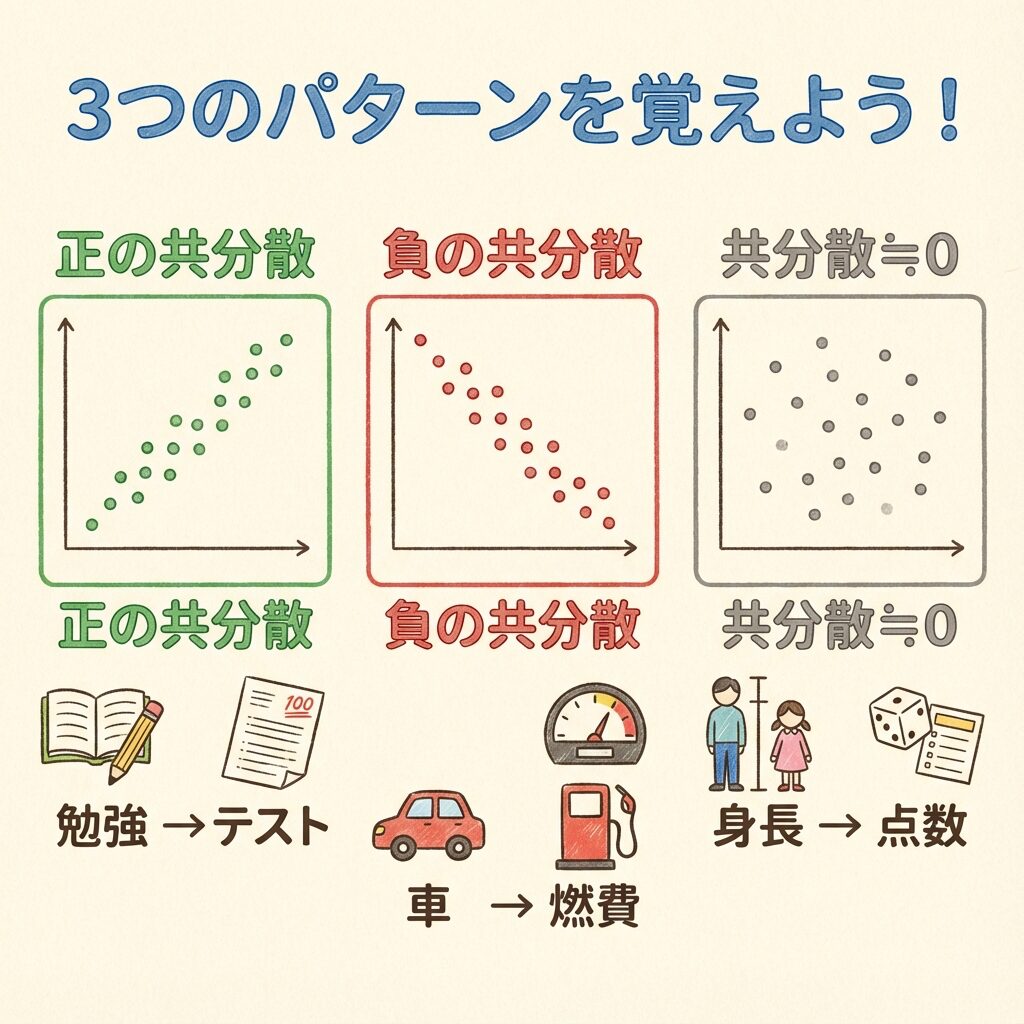
3つのパターンを「シーソー」で理解する
共分散には3つのパターンがあります。シーソーで考えると、一発で理解できます。
🟢 パターン①:正の共分散(一緒に動く仲良しさん)
イメージ:2人で一緒にジャンプ!
Aが上がる → Bも上がる ⬆️⬆️
Aが下がる → Bも下がる ⬇️⬇️
身近な例:
📚 勉強時間 ↔ テストの点数
💪 運動量 ↔ 筋肉量
📺 広告費 ↔ 売上
👔 経験年数 ↔ 給料
🔴 パターン②:負の共分散(シーソーの関係)
イメージ:シーソーに乗った2人!
Aが上がる → Bは下がる ⬆️⬇️
Aが下がる → Bは上がる ⬇️⬆️
身近な例:
🚗 車の価格 ↔ 燃費(高い車ほど燃費悪い傾向)
🌡️ 気温 ↔ 暖房費(暑くなれば暖房使わない)
🛒 価格 ↔ 需要(高いと売れにくい)
📉 株価 ↔ VIX指数(株が下がると恐怖指数UP)
⚪ パターン③:共分散≒0(無関係な2人)
イメージ:別々の場所で勝手に動く2人
Aが上がっても → Bは関係なく自由に動く
Aが下がっても → Bは関係なく自由に動く
身近な例:
📏 身長 ↔ 数学の点数(関係ない!)
👟 靴のサイズ ↔ 年収(関係ない!)
🎂 誕生月 ↔ 性格(関係ない!)
📞 電話番号 ↔ 体重(関係ない!)
共分散 > 0(正):同じ方向に動く
共分散 < 0(負):逆方向に動く
共分散 ≒ 0:関係なし
「点の雲」を読む!はじめての散布図ガイド →
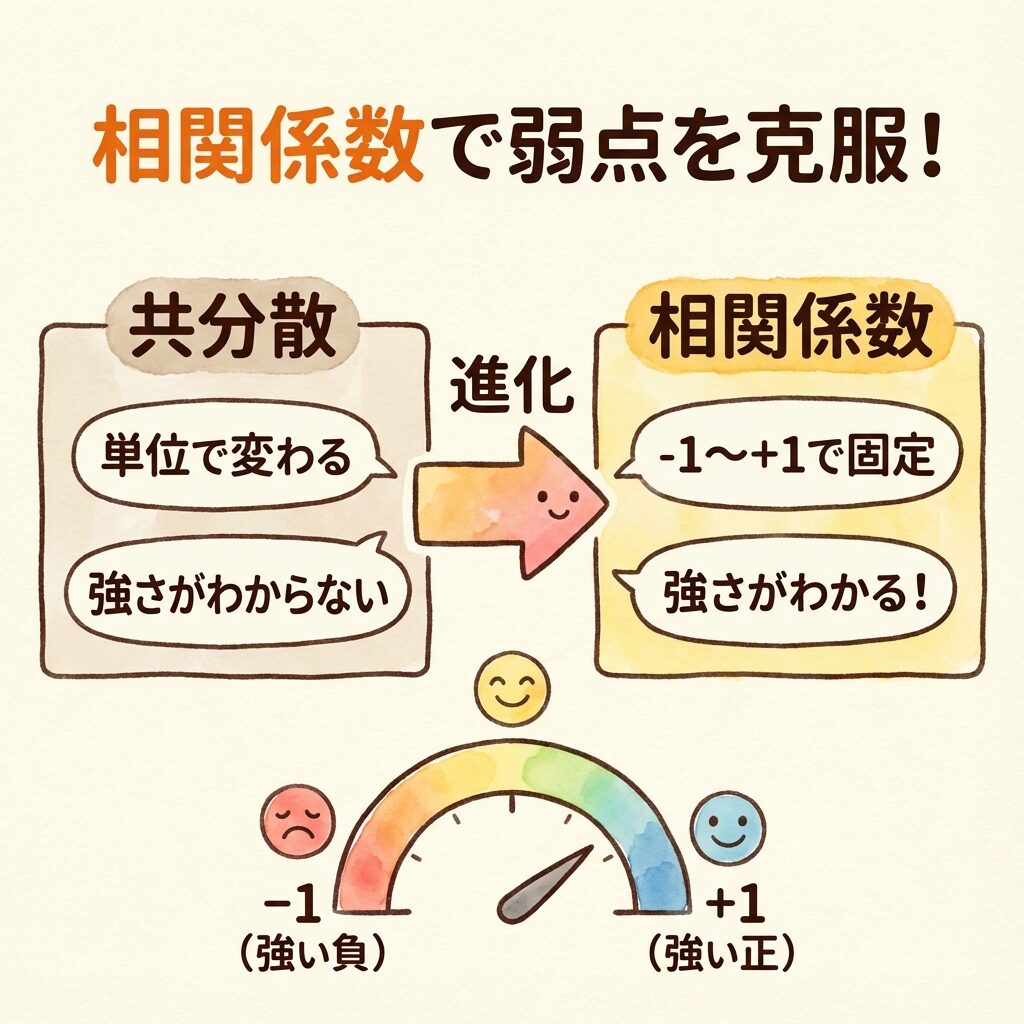
共分散の「弱点」と解決策
ここまで読んで、「共分散って便利!」と思ったかもしれません。でも、共分散には致命的な弱点があるんです。
❌ 弱点①:単位によって値が変わる
同じデータなのに、単位を変えると共分散の値が変わってしまいます。
気温を「℃」で測った場合 → 共分散 = 610
気温を「華氏」で測った場合 → 共分散 = 1,098
→ 同じ関係なのに、数値が全然違う!
❌ 弱点②:「強い」のか「弱い」のかわからない
共分散 = 610 と言われても、「それって強い関係?弱い関係?」が判断できません。
身長と体重の共分散が100、気温と売上の共分散が600だとして、「どっちが強い関係?」と聞かれても、答えられないのです。
✅ 解決策:相関係数の登場!
この弱点を解決するのが「相関係数」です。
相関係数 = 共分散 ÷ (Xの標準偏差 × Yの標準偏差)
相関係数は必ず「−1 〜 +1」の範囲に収まります。だから「強さ」が比較できる!
| 相関係数 | 解釈 |
|---|---|
| +0.8 〜 +1.0 | とても強い正の相関 |
| +0.6 〜 +0.8 | 強い正の相関 |
| +0.4 〜 +0.6 | 中程度の正の相関 |
| −0.2 〜 +0.2 | ほぼ無相関 |
| −0.8 〜 −1.0 | とても強い負の相関 |
共分散:方向(正 or 負 or ゼロ)はわかるけど、強さはわからない
相関係数:方向も強さもわかる!
→ だから実務では「相関係数」を使うことが多い
相関係数(r)と決定係数(R²)の不思議な関係|なぜ2乗すると一致するのか? →
⚠️ 超重要!「相関≠因果」の落とし穴
共分散(や相関係数)を使うとき、絶対に忘れてはいけない注意点があります。
🍦 有名な例:アイスと水難事故
こんなデータがあります。
「アイスクリームの売上」と「水難事故の件数」には強い正の相関がある
これを見て、こう結論づけたらどうでしょう?
❌ 間違った解釈:「アイスを食べると水難事故が起きる!」
もちろん、これは間違いですよね。
正しい解釈はこうです。
⭕ 正しい解釈:「夏という第3の要因が、アイス売上と水難事故の両方を増やしている」
このように、「見えない第3の要因」が両方に影響しているケースを「擬似相関(ぎじそうかん)」と呼びます。
【統計学】因果関係と相関関係の違いは?「擬似相関」の罠をアイスクリームの例で解説 →
【統計学】「アイスが売れると事故が増える?」擬似相関の罠と、データに騙されないための思考法 →
まとめ|共分散を味方につけよう
📊 共分散とは?
2つのデータの「仲良し度」を数値化したもの。一緒に動くかどうかを測る道具。
🔢 3つのパターン
正の共分散:一緒に上がる・一緒に下がる(仲良し!)
負の共分散:片方が上がると、もう片方は下がる(シーソー!)
共分散≒0:お互いに関係なし(他人!)
⚠️ 注意点
✅ 共分散は「方向」はわかるが「強さ」はわからない → 相関係数を使おう
✅ 相関があっても因果とは限らない → 「擬似相関」に注意!
共分散は、統計学の中でも「2つのデータの関係を見る」という超重要な概念の入口です。これがわかると、回帰分析や分散分析など、より高度な分析の理解もスムーズになります。