💭 こんな疑問、ありませんか?
- 「1時間に何回お客さんが来るか」を予測したい
- 「1日に何件クレームが入るか」を知りたい
- ポアソン分布って何?二項分布と何が違うの?
✅ この記事でスッキリ解決!
「コンビニのレジ」「LINEの通知」など身近な例えで、ポアソン分布を完全マスターできます!
📌 この記事の結論(先に知っておこう!)
ポアソン分布は「めったに起きないけど、たまに起きること」を予測するための道具です。「1時間に平均3回電話が鳴る」とき、「5回鳴る確率は?」「0回の確率は?」を計算できます。平均λ(ラムダ)さえわかれば、未来が予測できる魔法の分布です!
目次
🎯 ポアソン分布って何?|一言でいうと
ポアソン分布を一言で説明すると…
「めったに起きないこと」が
「一定期間に何回起きるか」を予測する道具
もう少し具体的に言うと、こんな場面で使います。
📞
コールセンター
1時間に何回電話が鳴る?
🏭
工場の品質管理
1日に何個の不良品が出る?
🚗
交通事故
1週間に何件事故が起きる?
🛒
コンビニのレジ
10分間に何人お客さんが来る?
共通点は「めったに起きないけど、たまに起きること」を数えていることです。

📱 身近な例で理解しよう|LINEの通知
ポアソン分布を、スマホの通知で考えてみましょう。
📱 あなたのスマホの1日を観察すると…
「1時間あたり平均2回、LINEの通知が来る」とわかりました。
では、次の1時間で…
- 通知が0回の確率は?
- 通知が3回の確率は?
- 通知が5回以上の確率は?
こういう予測ができるのが、ポアソン分布です!
🤔 なぜ「通知の回数」は予測できるの?
実は、こんな条件が揃っていれば、ポアソン分布で予測できます。
✅ ポアソン分布が使える3つの条件
① 平均的な発生率がわかっている
「1時間に平均2回」のように、平均がわかっている
② 各イベントは独立している
1回目の通知が来たからって、2回目が来やすくなるわけではない
③ 同時に複数回は起きない
同じ瞬間に2つの通知が同時に来ることはない

🔑 λ(ラムダ)って何?|たった1つのパラメータ
ポアソン分布で最も大切なのがλ(ラムダ)です。
λ = 平均発生回数
「一定期間に、平均して何回起きるか」を表す数字
λさえわかれば、ポアソン分布の形が決まります!
🎯 λの具体例
| 場面 | λの意味 | λの値 |
|---|---|---|
| コールセンター | 1時間あたりの平均着信数 | λ = 5 |
| 工場の不良品 | 1日あたりの平均不良品数 | λ = 2 |
| 交差点の事故 | 1週間あたりの平均事故数 | λ = 0.5 |
| Webサイトのエラー | 1時間あたりの平均エラー数 | λ = 0.3 |
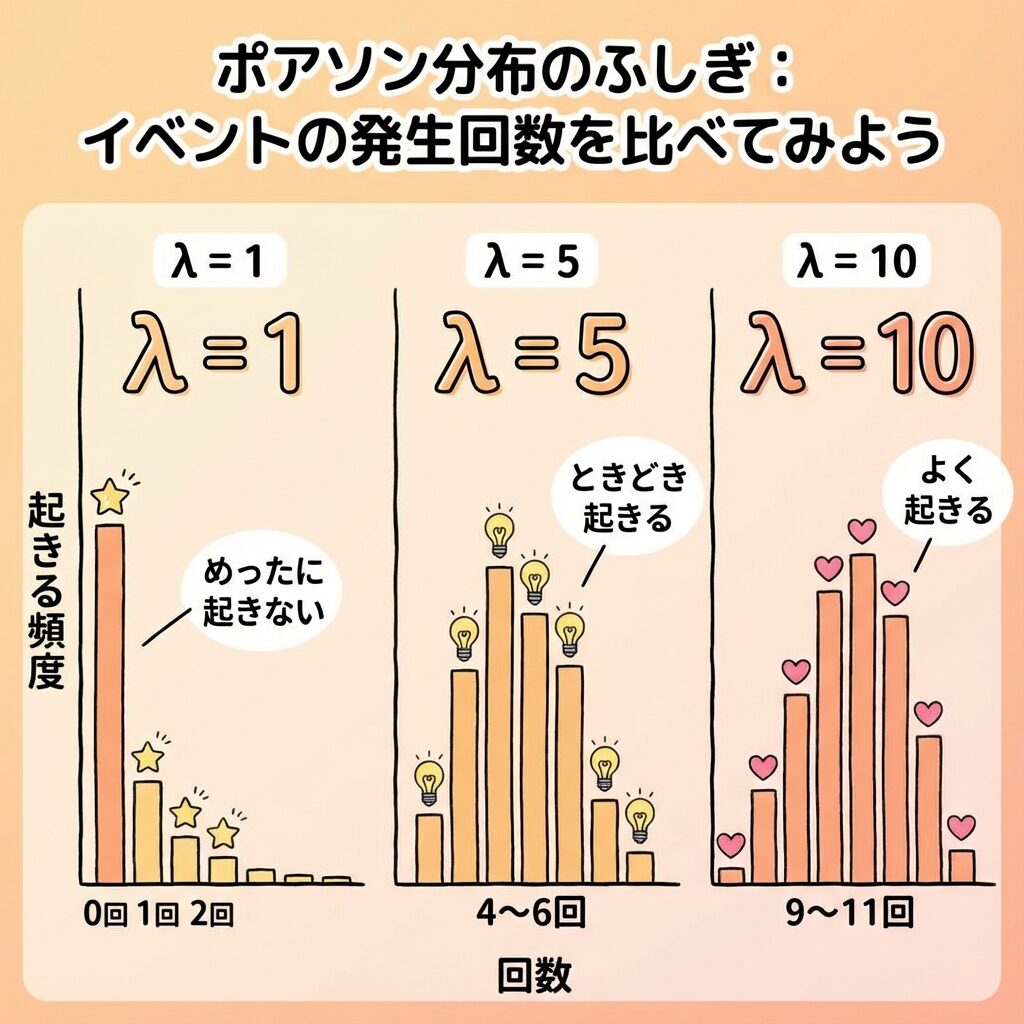
📊 λが変わると、分布の形も変わる
λの値によって、ポアソン分布のグラフの形が変わります。
λ = 1(めったに起きない)
0回が一番多い
右に裾が長い形
λ = 5(ときどき起きる)
5回付近が一番多い
山型に近づく
λ = 10(よく起きる)
10回付近が一番多い
左右対称に近い
💡 ポイント:λが大きくなると、ポアソン分布は正規分布に近づきます。λ ≥ 10 くらいから、ほぼ左右対称の山型になります。
📐 ポアソン分布の公式|意味をイメージで理解
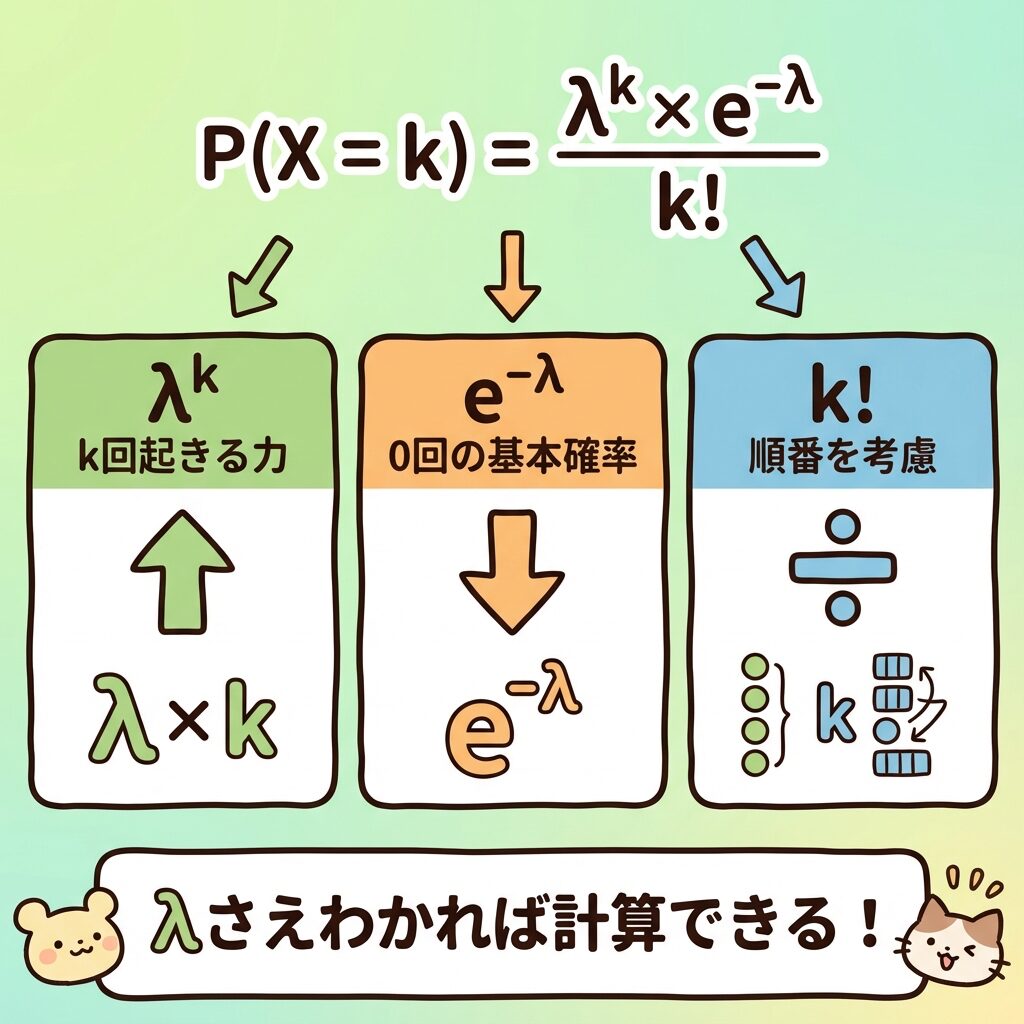
ポアソン分布の確率を求める公式を見てみましょう。
P(X = k) = (λᵏ × e⁻λ) / k!
公式を見ると難しそうですが、各パーツの意味を理解すればシンプルです!
🧩 公式を分解してみよう
λᵏ(ラムダのk乗)
「k回起きる可能性」を表す。k回起きるには、イベントがk回発生する必要がある。
e⁻λ(eのマイナスλ乗)
「0回起きる確率」の基本部分。λが大きいほど、0回の確率は下がる。
k!(kの階乗)
k回起きる「順番」を考慮して割る。3回なら 3! = 3×2×1 = 6 で割る。
💡 覚え方のコツ
公式を丸暗記するより、「λ(平均)さえわかれば計算できる」ということを覚えましょう。実際の試験では、電卓や公式表を使えることが多いです。
✏️ 計算例|実際に確率を求めてみよう
📝 例題
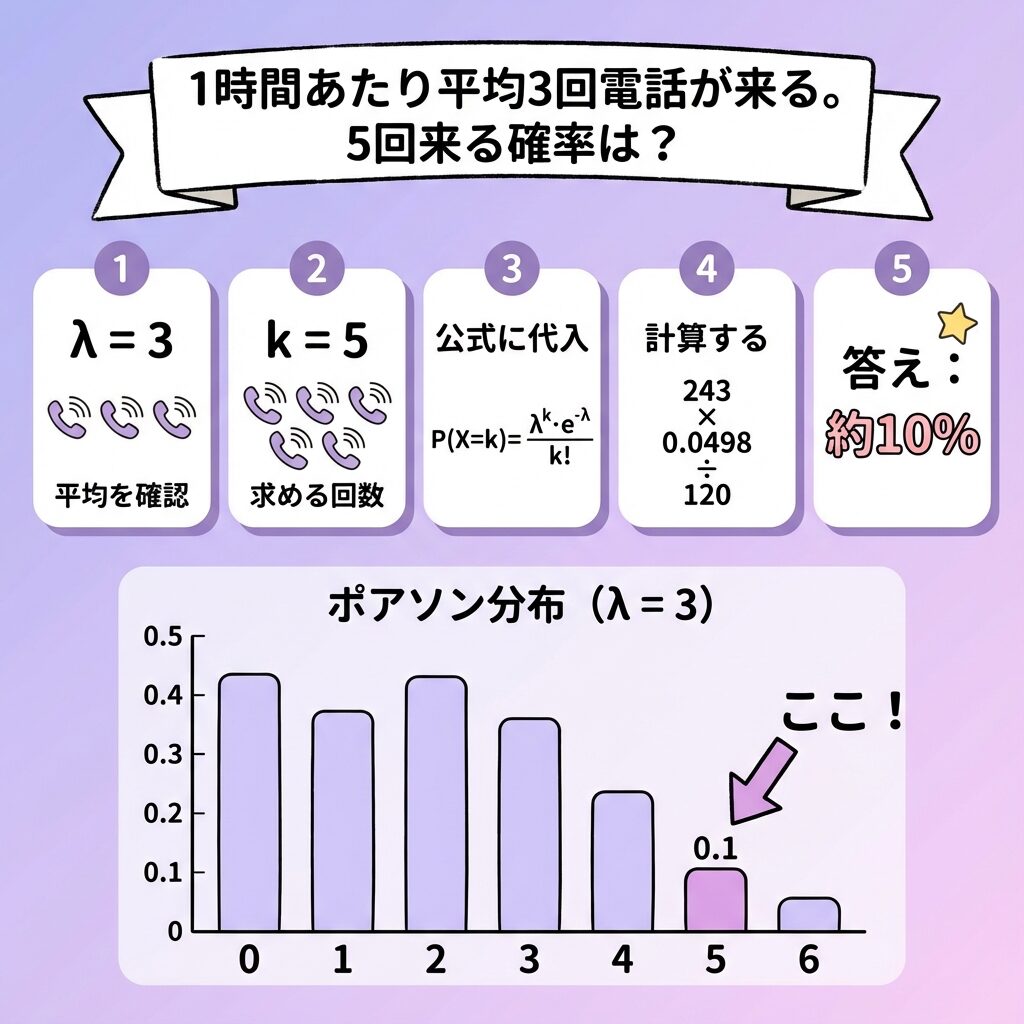
あるコールセンターでは、1時間あたり平均3回の電話がかかってきます。
次の1時間で、電話がちょうど5回かかってくる確率を求めなさい。
📋 解き方ステップ
λを確認する
問題文から「1時間あたり平均3回」なので、λ = 3
kを確認する
「ちょうど5回」なので、k = 5
公式に代入する
P(X = 5) = (3⁵ × e⁻³) / 5!
各パーツを計算する
3⁵ = 243
e⁻³ ≒ 0.0498
5! = 120
答えを出す
P(X = 5) = (243 × 0.0498) / 120 ≒ 0.101
答え:約10.1%(約10回に1回)
平均3回のところに5回電話がかかってくる確率は、意外と低くないですね!
📊 他の回数の確率も見てみよう
λ = 3のとき、各回数の確率はこうなります。
| 回数 k | 0回 | 1回 | 2回 | 3回 | 4回 | 5回 |
|---|---|---|---|---|---|---|
| 確率 | 5.0% | 14.9% | 22.4% | 22.4% | 16.8% | 10.1% |
平均λ = 3のとき、2回と3回が最も起きやすく、0回や6回以上は起きにくいことがわかります。
🔗 二項分布との関係|ポアソン分布の正体
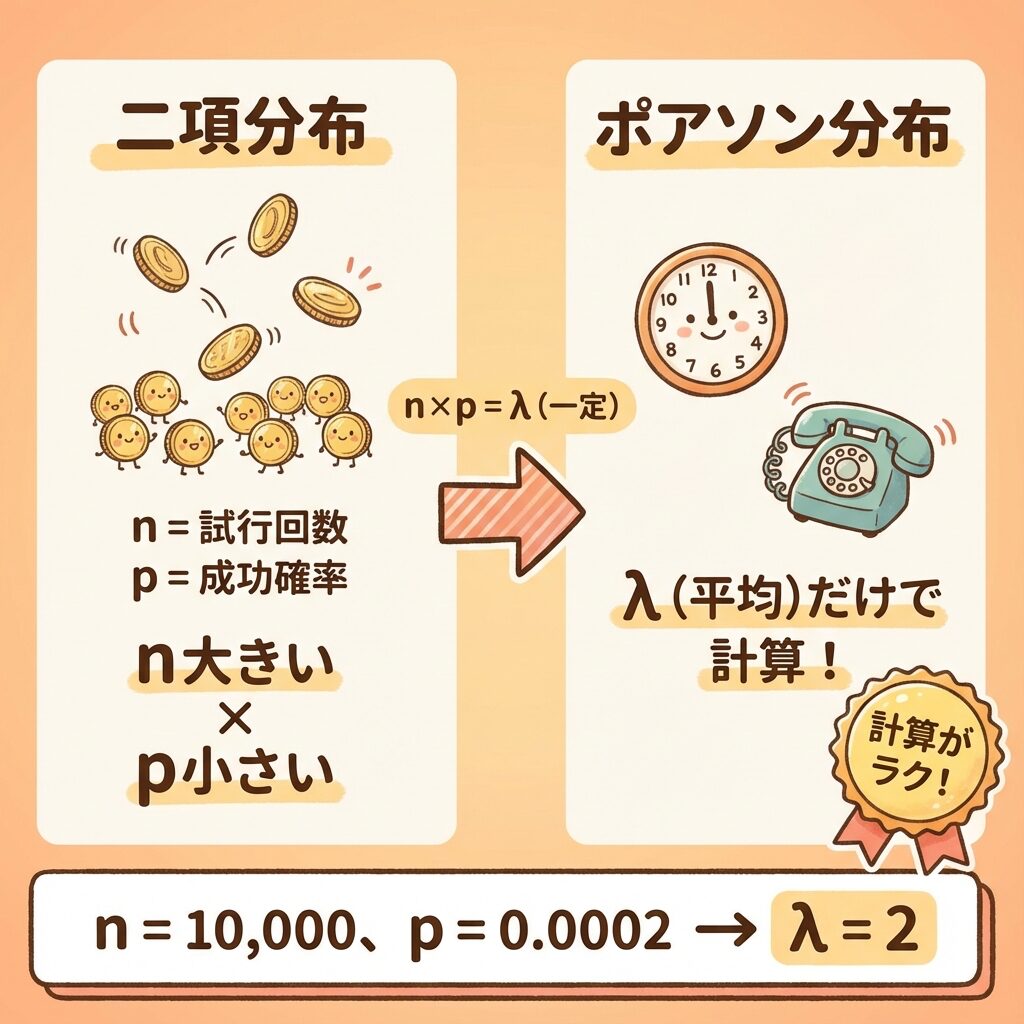
実は、ポアソン分布は二項分布の「特殊なケース」なんです。
🎯 ポアソン分布が生まれる条件
試行回数 n
とても大きい
×
成功確率 p
とても小さい
n × p = λ(一定)のとき、二項分布はポアソン分布に近づく!
🏭 工場の不良品で理解しよう
📦 具体例
ある工場では、1日に10,000個の製品を作っています。
不良品率は0.02%(0.0002)と非常に低いです。
このとき、1日の不良品の数は?
二項分布で計算すると…
n = 10,000
p = 0.0002
→ 計算がとても大変!😵
ポアソン分布で近似すると…
λ = n × p = 10,000 × 0.0002 = 2
→ λ = 2 で簡単に計算できる!😊
💡 使い分けのポイント:試行回数nが大きく(目安:n ≥ 100)、確率pが小さい(目安:p ≤ 0.1)とき、ポアソン分布で近似すると計算が楽になります!
📊 ポアソン分布の性質|覚えておきたいポイント
✨ ポアソン分布の3つの重要な性質
① 平均 = 分散 = λ
ポアソン分布では、平均と分散が同じ値λになります。
E(X) = λ、V(X) = λ
② 再生性がある
λ₁のポアソン分布 + λ₂のポアソン分布 = λ₁+λ₂のポアソン分布
1時間で平均3回 + 1時間で平均2回 = 2時間で平均5回
③ λが大きいと正規分布に近づく
λ ≥ 10 くらいになると、正規分布N(λ, λ)で近似できます。
平均 = 分散 = λ
これがポアソン分布の最大の特徴!
平均と分散が同じ値になる。
✅ まとめ|ポアソン分布のポイント
📝 試験で覚えるべきこと
① ポアソン分布とは?
「めったに起きないこと」が「一定期間に何回起きるか」を予測する分布
② λ(ラムダ)とは?
平均発生回数。これ1つで分布が決まる!
③ 公式
P(X = k) = (λᵏ × e⁻λ) / k!
④ 二項分布との関係
nが大きく、pが小さいとき、二項分布はポアソン分布で近似できる
⑤ 最大の特徴
平均 = 分散 = λ(平均と分散が一致する)
📚 確率分布シリーズ|あわせて読みたい
🎯 QC検定での出題ポイント
ポアソン分布はQC検定2級・3級で頻出のテーマです。特に以下の点を押さえておきましょう。
- 不良品数や欠点数など「計数値」のモデル化
- 二項分布との使い分け(nが大きく、pが小さい場合)
- 平均と分散が等しいという特徴