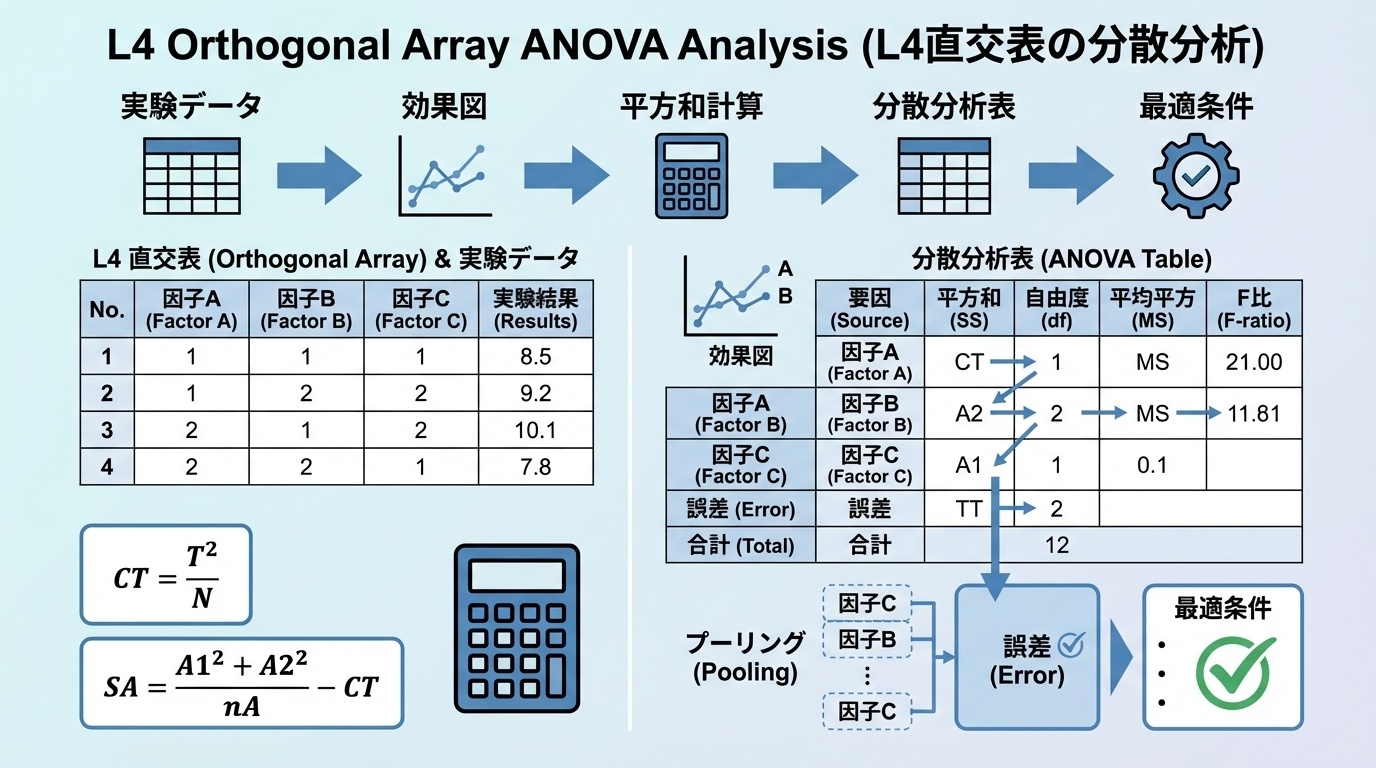
💡 こんな悩みはありませんか?
✅「L4直交表で実験したけど、そのあとどうすればいいの?」
✅「分散分析って必要なの?何のためにやるの?」
✅「最適条件ってどうやって導き出すの?」
✅「計算式は見たけど、なぜそうするのかがわからない…」
🎯 この記事を読むとわかること
✔ L4直交表のデータから「最適条件」を導く全手順
✔ なぜその計算が必要なのか?を直感的に理解できる
✔ 分散分析表の作り方を1ステップずつ丁寧に学べる
✔ どの因子が「本当に効いている」かを判定する方法
✔ 最適条件での性能を予測する方法
目次
🌟 はじめに:L4直交表の実験が終わったら、次は何をする?
L4直交表を使って実験を終えたあなた。手元には4回分の実験データがあります。
【あなたの状況】
📊 L4直交表で4回の実験を実施
📈 3つの因子(A・B・C)を調べた
❓ 疑問:「このデータから、どの因子が効いてる?最適な条件は?」
実は、実験データをそのまま眺めるだけでは、正しい答えは見つかりません。
❌ よくある間違い
「実験No.3の結果が一番良かったから、No.3の条件が最適!」
→ これは間違いです!
なぜなら、その結果は「偶然」かもしれないからです。
そこで必要になるのが、分散分析です。
この記事では、L4直交表のデータから「統計的に正しい最適条件」を導く全手順を、初心者にもわかるように1ステップずつ解説します!
📋 今回使う実験データ
実験の背景
🧪 実験の目的
製品の「引張強度」を高めたい!
調べる因子(3つ):
🅰️ 因子A:成形温度(A1=低温、A2=高温)
🅱️ 因子B:成形圧力(B1=低圧、B2=高圧)
©️ 因子C:冷却時間(C1=短時間、C2=長時間)
L4直交表への割り付けと実験結果
| 実験No. | 列1 因子A (温度) |
列2 因子B (圧力) |
列3 因子C (冷却) |
結果 引張強度 (kg/cm²) |
|---|---|---|---|---|
| 1 | 1(低温) | 1(低圧) | 1(短時間) | 45 |
| 2 | 1(低温) | 2(高圧) | 2(長時間) | 52 |
| 3 | 2(高温) | 1(低圧) | 2(長時間) | 50 |
| 4 | 2(高温) | 2(高圧) | 1(短時間) | 49 |
👉 L4直交表の基本については「L4直交表・L8直交表の使い方」で学べます。
💡 分散分析の全体像:なぜ必要なのか?
分散分析って何?
分散分析(ANOVA)とは、「データのばらつき」を分解して、「どの因子が本当に効いているか」を統計的に判定する方法です。
🎯 分散分析の目的
✅ 目的1:どの因子が「本当に効いている」かを見極める
✅ 目的2:「偶然」と「本物の効果」を区別する
✅ 目的3:最適条件での性能を予測する
なぜ「ばらつき」を分解するの?
実験データには、必ず「ばらつき」があります。このばらつきには2種類あります。
📊 データのばらつき = ❶本物の効果 + ❷偶然の誤差
❶ 本物の効果:
因子A(温度)を変えたから強度が変わった(意味のある変化)
❷ 偶然の誤差:
測定のブレ、材料のバラツキなど(意味のない変化)
分散分析は、この2つを数学的に分離して、「本物の効果」だけを取り出す技術なのです!
分散分析の流れ(全体像)
📐 分散分析の5ステップ
STEP 1:要因効果図を描く(視覚的に理解)
STEP 2:平方和を計算する(ばらつきの量を数値化)
STEP 3:分散分析表を作る(効果を整理)
STEP 4:F検定で判定する(効果の有無を統計的に判断)
STEP 5:最適条件を決定する(性能を予測)
それでは、1ステップずつ丁寧に見ていきましょう!
📈 【STEP 1】要因効果図を描く
要因効果図って何?
要因効果図とは、各因子の水準ごとの平均値をグラフで表したものです。視覚的に「どの因子が効いているか」を把握できます。
💡 なぜ要因効果図を描くのか?
✅ 計算前に「感覚」をつかむため
✅ どの因子の傾きが大きいか(効果が強いか)を視覚化
✅ グラフが平らな因子は「効果が弱い」とすぐわかる
水準別平均を計算する
まず、各因子の水準1と水準2の平均値を計算します。
📊 因子Aの水準別平均
A1(低温):実験No.1とNo.2 → (45 + 52) / 2 = 48.5
A2(高温):実験No.3とNo.4 → (50 + 49) / 2 = 49.5
📊 因子Bの水準別平均
B1(低圧):実験No.1とNo.3 → (45 + 50) / 2 = 47.5
B2(高圧):実験No.2とNo.4 → (52 + 49) / 2 = 50.5
📊 因子Cの水準別平均
C1(短時間):実験No.1とNo.4 → (45 + 49) / 2 = 47.0
C2(長時間):実験No.2とNo.3 → (52 + 50) / 2 = 51.0
要因効果図の解釈
📈 要因効果図から読み取れること
因子A(温度):48.5 → 49.5(差:1.0)
→ 傾きが緩やか。効果は小さい。
因子B(圧力):47.5 → 50.5(差:3.0)
→ 傾きがやや大きい。効果あり。
因子C(冷却):47.0 → 51.0(差:4.0)
→ 傾きが最も大きい。効果が強い!
要因効果図から、「因子C(冷却時間)が最も効果が大きそう」という感覚がつかめました。
でも、これだけでは不十分です。「この差は偶然ではない」と統計的に証明する必要があります。
👉 主効果とは?で要因効果図の詳細を学べます。
🔢 【STEP 2】平方和を計算する
平方和って何?なぜ必要?
平方和(Sum of Squares)とは、「データのばらつきの量」を数値化したものです。
💡 なぜ平方和を計算するのか?
✅ 各因子が「どれだけ強く効いているか」を数値で比較するため
✅ 「本物の効果」と「偶然の誤差」の大きさを比べるため
✅ グラフだけでは「感覚」しかわからないが、数値化すれば「統計的に証明」できる
STEP 2-1:修正項(CT)の計算
修正項(CT)は、すべての計算のベースになる値です。
📐 修正項の計算式
CT = (全データの合計)² / データ数
🔢 計算
全データの合計:45 + 52 + 50 + 49 = 196
データ数:4
CT = 196² / 4 = 38,416 / 4
CT = 9,604
STEP 2-2:総平方和(ST)の計算
総平方和(ST)は、全データのばらつきの総量です。
📐 総平方和の計算式
ST = (各データ²の合計) - CT
🔢 計算
45² + 52² + 50² + 49² = 2,025 + 2,704 + 2,500 + 2,401 = 9,630
ST = 9,630 - 9,604
ST = 26
STEP 2-3:各因子の平方和(SA, SB, SC)の計算
各因子の平方和は、その因子が生み出すばらつきの量を表します。
📐 因子の平方和の計算式
S因子 = (水準1の合計² / 水準1のデータ数) + (水準2の合計² / 水準2のデータ数) - CT
📊 因子A(温度)の平方和
A1の合計:45 + 52 = 97(データ数2)
A2の合計:50 + 49 = 99(データ数2)
SA = (97² / 2) + (99² / 2) - 9,604
SA = (9,409 / 2) + (9,801 / 2) - 9,604
SA = 4,704.5 + 4,900.5 - 9,604
SA = 1
📊 因子B(圧力)の平方和
B1の合計:45 + 50 = 95(データ数2)
B2の合計:52 + 49 = 101(データ数2)
SB = (95² / 2) + (101² / 2) - 9,604
SB = (9,025 / 2) + (10,201 / 2) - 9,604
SB = 4,512.5 + 5,100.5 - 9,604
SB = 9
📊 因子C(冷却)の平方和
C1の合計:45 + 49 = 94(データ数2)
C2の合計:52 + 50 = 102(データ数2)
SC = (94² / 2) + (102² / 2) - 9,604
SC = (8,836 / 2) + (10,404 / 2) - 9,604
SC = 4,418 + 5,202 - 9,604
SC = 16
💡 平方和の比較から見えること
SA = 1(小さい)→ 因子Aの効果は弱い
SB = 9(中くらい)→ 因子Bの効果はまあまあ
SC = 16(大きい)→ 因子Cの効果が最も強い!
STEP 2-4:誤差の平方和(Se)の計算
誤差(Se)は、因子では説明できない「偶然のばらつき」です。
📐 誤差の平方和の計算式
Se = ST - SA - SB - SC
(引き算で求まります!)
🔢 計算
Se = ST - SA - SB - SC
Se = 26 - 1 - 9 - 16
Se = 0
💡 Se = 0 の意味
誤差がゼロ?これは「繰り返し実験をしていない」ため起こります。
L4直交表では、繰り返しなしのため、誤差を直接計算できません。
→ 次のステップで「プーリング」という手法を使います。
👉 プーリングとは?で詳しく学べます。
📊 【STEP 3】分散分析表を作る
自由度を計算する
自由度は、「自由に決められる数の個数」です。
📐 自由度の計算
総自由度:φT = n - 1 = 4 - 1 = 3
各因子の自由度:φ = 水準数 - 1 = 2 - 1 = 1
→ φA = 1、φB = 1、φC = 1
プーリング(誤差への併合)
Se = 0 では分散分析ができません。そこで、効果の小さい因子を「誤差」として扱います。これをプーリングといいます。
💡 なぜプーリングするのか?
✅ 効果が小さい因子は「偶然のばらつき」と区別できない
✅ 誤差に併合することで、F検定ができるようになる
今回は、因子A(SA = 1)が最も小さいので、これを誤差にプーリングします。
🔢 プーリング後の誤差
Se' = Se + SA = 0 + 1 = 1
φe' = φe + φA = 0 + 1 = 1
平均平方(分散)を計算する
平均平方(V)は、「1自由度あたりのばらつき」を表します。
📐 平均平方の計算式
V = S / φ
🔢 計算
VB:9 / 1 = 9
VC:16 / 1 = 16
Ve:1 / 1 = 1
F値を計算する
F値は、「効果」÷「誤差」の比率です。F値が大きいほど「効果がある」と言えます。
📐 F値の計算式
F = V(因子) / Ve(誤差)
🔢 計算
FB:9 / 1 = 9
FC:16 / 1 = 16
分散分析表の完成!
| 要因 | 平方和(S) | 自由度(φ) | 平均平方(V) | F値 |
|---|---|---|---|---|
| 因子B(圧力) | 9 | 1 | 9 | 9 |
| 因子C(冷却) | 16 | 1 | 16 | 16 |
| 誤差(e) ※因子Aをプーリング |
1 | 1 | 1 | — |
| 総計(T) | 26 | 3 | — | — |
🎉 分散分析表が完成しました!
次は、F検定で「どの因子が統計的に有意か」を判定します。
👉 分散分析表の作り方完全ガイドで理論を深められます。
🔍 【STEP 4】F検定で判定する
F検定って何?
F検定とは、「この効果は偶然ではない」と統計的に証明する方法です。
💡 F検定の考え方
✅ F値が大きい → 「偶然では起こりにくい」→ 効果あり
✅ F値が小さい → 「偶然で説明できる」→ 効果なし
F分布表の「臨界値」と比較して判定します。
F分布表で臨界値を確認
有意水準5%(α=0.05)のF分布表を使います。
📊 F分布表の値
自由度(φ因子=1, φe=1)、α=0.05の場合
F0.05(1, 1) = 161.4
判定結果
| 要因 | F値 | F0.05の臨界値 | 判定 |
|---|---|---|---|
| 因子B(圧力) | 9 | 161.4 | 有意でない |
| 因子C(冷却) | 16 | 161.4 | 有意でない |
⚠️ 判定結果
どちらの因子も「統計的に有意ではない」という結果になりました。
原因:データ数が少なすぎる(n=4)ため、誤差の自由度が小さく、臨界値が非常に大きくなっています。
🎯 【STEP 5】最適条件を決定する
最適条件の選び方
F検定の結果に関わらず、平方和が大きい因子は「効果がある」と考えられます。
📊 要因効果図から最適水準を選ぶ
因子A(温度):A2(高温)の方がやや高い → A2を選択
因子B(圧力):B2(高圧)の方が高い → B2を選択
因子C(冷却):C2(長時間)の方が高い → C2を選択
✅ 最適条件
A2(高温)× B2(高圧)× C2(長時間)
最適条件での性能予測
最適条件での引張強度を予測します。
📐 予測式
予測値 = 全体平均 + (A2の効果) + (B2の効果) + (C2の効果)
🔢 計算
全体平均:196 / 4 = 49.0
A2の効果:49.5 - 49.0 = +0.5
B2の効果:50.5 - 49.0 = +1.5
C2の効果:51.0 - 49.0 = +2.0
予測値 = 49.0 + 0.5 + 1.5 + 2.0
予測値 = 53.0 kg/cm²
✅ 結論
最適条件「A2×B2×C2」で実験すれば、引張強度約53.0 kg/cm²が期待できます。
これは実験データの最大値(52)を上回る予測です!
👉 母平均の推定で予測の詳細を学べます。
📝 まとめ
✅ この記事のポイント
🔹 L4直交表の分散分析で、どの因子が効いているかを統計的に分析できる
🔹 要因効果図で視覚的に理解 → 平方和で数値化 → F検定で統計的判定
🔹 プーリングで効果の小さい因子を誤差に併合する
🔹 最適条件の予測で、実験していない組み合わせの性能を推定できる
🔹 L4はスクリーニングに使い、重要因子は追加実験で詳しく調べる
🎓 さらに学びを深めるには
📌 L4直交表・L8直交表の使い方で基礎を復習
📌 直交配列表とは?で直交表の仕組みを理解
📌 分散分析表の作り方完全ガイドで理論を深める
📌 二元配置実験で重要因子を詳しく分析
📌 実験計画法の学習マップで体系的に学習
🚀 次の記事へ
📖 次はこちらの記事がおすすめ!
L4直交表の分散分析をマスターした次は、「より多くの因子を調べる方法」を学びましょう。
👉 次の記事:L8直交表の使い方|7因子を8回の実験で調べる
🔹 L8直交表を理解すると、最大7因子まで効率的に実験できるようになります!
📚 実験計画法の「挫折」を救う2冊
「数式を見た瞬間に本を閉じた」
そんな経験がある私だからこそ推せる、厳選のバイブルです。