電験三種の「理論」科目で必ず出題されるコンデンサの静電容量。公式「C=εS/d」は知っているけど、「なぜこの式になるのか?」「誘電体を挿入したらどうなるの?」と疑問に思ったことはありませんか?
この記事では、コンデンサの静電容量について、公式の丸暗記ではなく「導出から理解する」アプローチで徹底解説します。試験に頻出する直列・並列接続の計算、そして多くの受験者が苦手とする「誘電体挿入問題」まで、合格に必要な知識をすべてカバーします。
公式の意味を理解すれば、応用問題にも対応できるようになります。一緒に学んでいきましょう!
目次
⚡ こんな悩みを解決します
- ✅ C=εS/dの公式、なぜこの形なのか理解したい
- ✅ 直列・並列接続の合成容量の計算方法がわからない
- ✅ 誘電体挿入問題が出ると手が止まってしまう
- ✅ ε(イプシロン)、ε₀、εᵣの違いがあいまい
📖 この記事を読むとわかること
- 静電容量C=εS/dの公式の導出過程と物理的意味
- 誘電率ε、面積S、距離dがそれぞれ何を表すのか
- 直列・並列接続の合成容量の計算方法(覚え方付き)
- 過去問頻出!誘電体挿入問題の解き方
- 試験本番で使える計算テクニック
🔋 コンデンサと静電容量の基礎
📌 コンデンサとは何か?
コンデンサ(キャパシタ)は、電気エネルギーを蓄える電子部品です。基本的な構造は非常にシンプルで、2枚の金属板(電極板)を平行に配置し、その間に絶縁体を挟んだものです。
💡 身近な例
スマートフォンのフラッシュ、カメラのストロボ、電源回路など、あらゆる電子機器に使われています。瞬間的に大きな電流を流す必要がある場面で活躍します。
📐 静電容量とは?
静電容量(Capacitance)は、コンデンサがどれだけ電荷を蓄えられるかを表す能力のことです。記号はC、単位はF(ファラド)で表します。
定義式:
C = Q / V
C:静電容量 [F]
Q:蓄えられる電荷 [C(クーロン)]
V:加えた電圧 [V(ボルト)]
つまり、「同じ電圧をかけたとき、より多くの電荷を蓄えられるコンデンサほど、静電容量が大きい」ということです。
🧮 公式C=εS/dを導出から理解する
📝 平行板コンデンサの構造
最も基本的な「平行板コンデンサ」を例に、公式を導出します。構造は以下の通りです:
- 2枚の平行な金属板(面積S [m²])
- 板の間隔d [m]
- 板の間には誘電体(誘電率ε)
🔬 公式の導出プロセス
ステップ1:平行板間の電界E
一方の板に+Q、もう一方に−Qの電荷を与えると、板の間に一様な電界Eが生じます。
E = Q / (ε × S)
ステップ2:電圧Vと電界Eの関係
平行板間の電圧Vは、電界Eと距離dの積で表されます。
V = E × d
ステップ3:Eを代入
ステップ1の式を代入します。
V = (Q / (ε × S)) × d = Q × d / (ε × S)
ステップ4:静電容量Cを求める
C = Q / Vの定義式より、
C = Q / V = Q / (Q × d / (ε × S)) = ε × S / d
完成!
C = εS / d
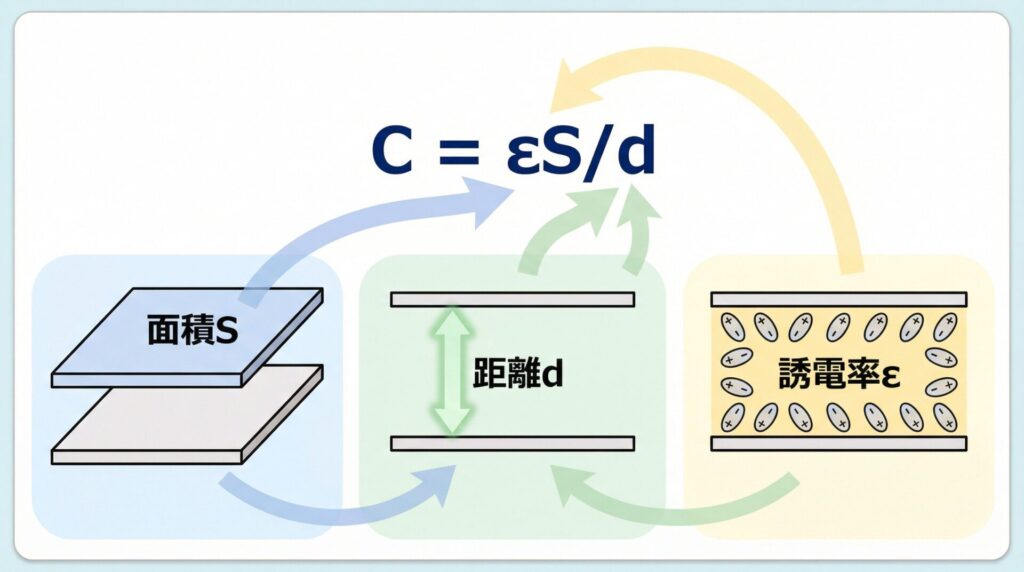
🔍 各パラメータの物理的意味
公式の各記号が何を表すのか、そしてどう変化すると静電容量がどうなるのかを理解しましょう。
1. ε(イプシロン):誘電率
意味:電極板の間にある物質(誘電体)の性質を表す値
単位:[F/m](ファラド毎メートル)
📊 関係:εが大きい → Cが大きくなる(比例)
つまり、誘電率の高い物質を挟むと、より多くの電荷を蓄えられます。
💡 誘電率の表記について
試験では3つの記号が出てきます:
• ε₀(イプシロン・ゼロ):真空の誘電率 = 8.85 × 10⁻¹² F/m
• εᵣ(イプシロン・アール):比誘電率(真空を1としたときの比)
• ε:誘電率 = ε₀ × εᵣ
試験でよく使うのはこの関係式です!
2. S:電極板の面積
意味:平行な2枚の電極板の向かい合っている部分の面積
単位:[m²]
📊 関係:Sが大きい → Cが大きくなる(比例)
板の面積が広いほど、たくさんの電荷を蓄えられます。「広い駐車場ほど車がたくさん停められる」イメージです。
3. d:電極板間の距離
意味:2枚の電極板の間隔
単位:[m]
📊 関係:dが大きい → Cが小さくなる(反比例)
板の間隔が広いほど、蓄えられる電荷は少なくなります。唯一の「分母」なので要注意です!
🎯 試験で覚えるべきポイント
C = εS / dの公式で:
• 分子(ε、S)が増える → Cが増える ✅
• 分母(d)が増える → Cが減る ⚠️
誘電体挿入問題では、この関係性が必ず問われます!
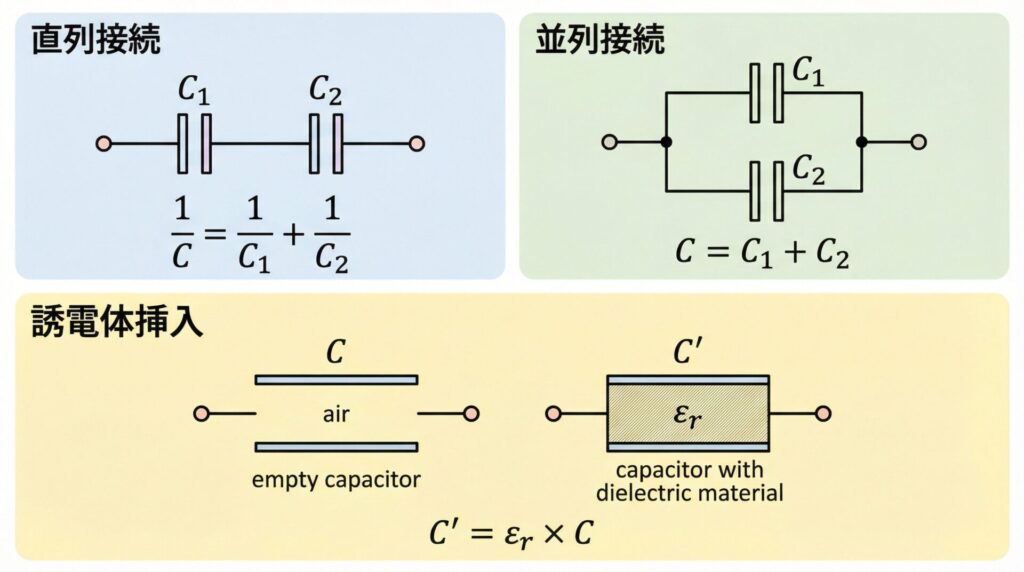
🔗 直列・並列接続の合成容量
複数のコンデンサを組み合わせたとき、全体としてどれだけの静電容量になるか?これが「合成容量」です。直列と並列で計算方法が異なるので、しっかり区別しましょう。
⚠️ 注意!抵抗の逆
コンデンサの合成容量は、抵抗の合成抵抗と逆の関係になります。混同しやすいので要注意です!
📊 並列接続の合成容量
並列接続の合成容量
C = C₁ + C₂ + C₃ + ...
覚え方:「並列は足すだけ!」
なぜこうなる?
並列接続では、各コンデンサに同じ電圧Vがかかります。蓄えられる電荷は各コンデンサで独立して蓄えられるため、総電荷Qtotalは各コンデンサの電荷の合計になります。
Qtotal = Q₁ + Q₂ + Q₃
両辺をVで割ると:C = C₁ + C₂ + C₃
💡 例題:並列接続
【例題】C₁ = 2μF、C₂ = 3μF、C₃ = 5μFのコンデンサを並列接続したとき、合成容量を求めよ。
【解答】
並列接続なので、単純に足すだけ!
C = C₁ + C₂ + C₃ = 2 + 3 + 5 = 10μF
意味:並列に接続すると、個々のコンデンサより大きな容量になります。
📊 直列接続の合成容量
直列接続の合成容量
1/C = 1/C₁ + 1/C₂ + 1/C₃ + ...
覚え方:「直列は逆数を足す!」(抵抗の並列と同じ形)
⚡ 2個の直列接続の簡易公式
試験で最も頻出なのは2個の直列接続です。この場合、以下の公式が使えます:
C = (C₁ × C₂) / (C₁ + C₂)
覚え方:「積を和で割る」(抵抗の並列と同じ!)
💡 例題:直列接続
【例題】C₁ = 6μF、C₂ = 3μFのコンデンサを直列接続したとき、合成容量を求めよ。
【解答】
2個の直列なので簡易公式を使います。
C = (C₁ × C₂) / (C₁ + C₂) = (6 × 3) / (6 + 3) = 18 / 9 = 2μF
意味:直列に接続すると、最も小さい容量よりさらに小さくなります。
📋 直列・並列の比較表
| 項目 | 並列接続 | 直列接続 |
|---|---|---|
| 合成容量の式 | C = C₁ + C₂ + ... | 1/C = 1/C₁ + 1/C₂ + ... |
| 計算方法 | 足すだけ | 逆数を足す |
| 合成容量の大きさ | 個々より大きくなる | 最小のものより小さくなる |
| 抵抗との関係 | 抵抗の直列と同じ形 | 抵抗の並列と同じ形 |
| 2個の簡易公式 | C = C₁ + C₂ | C = (C₁×C₂)/(C₁+C₂) |
⚠️ よくあるミス
❌ 並列と直列の公式を逆に覚えている
❌ 直列接続で逆数にするのを忘れる
❌ 2個の直列で「積を和で割る」公式を使い忘れる
試験では「並列=足す」「直列=逆数」を最初に確認しましょう!
⚡ 過去問頻出!誘電体挿入問題の攻略法
電験三種で多くの受験者が苦手とする「誘電体挿入問題」。でも、パターンを理解すれば確実に得点できます!
📌 誘電体挿入問題とは?
真空(または空気)の平行板コンデンサに、誘電率の高い物質(誘電体)を挿入すると、静電容量がどう変化するか?という問題です。
基本の考え方
C = εS / dの公式で、誘電率εが変化します。
• 挿入前:ε = ε₀(真空の誘電率)
• 挿入後:ε = ε₀ × εᵣ(εᵣは比誘電率)
つまり、静電容量はεᵣ倍になります!
🧮 誘電体挿入の公式
誘電体挿入後の静電容量
C' = εᵣ × C
C:挿入前の静電容量
C':挿入後の静電容量
εᵣ:誘電体の比誘電率
📚 試験で問われる3つのパターン
パターン1:電源につないだまま誘電体を挿入
特徴:電圧Vは一定(電源が維持する)
• 静電容量:C' = εᵣ × C (εᵣ倍に増加)
• 蓄えられる電荷:Q' = C' × V = εᵣ × C × V = εᵣ × Q (εᵣ倍に増加)
• 静電エネルギー:U' = (1/2)C'V² = εᵣ × U (εᵣ倍に増加)
パターン2:電源を切ってから誘電体を挿入
特徴:電荷Qは一定(逃げ場がない)
• 静電容量:C' = εᵣ × C (εᵣ倍に増加)
• 電圧:V' = Q / C' = Q / (εᵣ × C) = V / εᵣ (1/εᵣ倍に減少)
• 静電エネルギー:U' = (1/2)Q²/C' = U / εᵣ (1/εᵣ倍に減少)
パターン3:部分的に誘電体を挿入
特徴:コンデンサが2つに分割される(並列接続)
例:面積Sの半分に誘電体を挿入した場合
• 誘電体がある部分:C₁ = ε₀εᵣ × (S/2) / d
• 真空の部分:C₂ = ε₀ × (S/2) / d
• 合成容量:C' = C₁ + C₂(並列接続)
💡 例題で実践
【例題】静電容量10μFのコンデンサに100Vの電圧をかけて充電した後、電源を切り離してから比誘電率εᵣ=4の誘電体を挿入した。挿入後の電圧V'を求めよ。
【解答】
ステップ1:パターンを見極める
→ 電源を切り離してから挿入 → パターン2(電荷Q一定)
ステップ2:公式を使う
電荷Q一定のとき、V' = V / εᵣ
ステップ3:計算
V' = 100V / 4 = 25V
答え:25V(誘電体を挿入すると電圧は1/4に減少)
🎯 誘電体挿入問題の解き方
手順1:電源つないだまま? 切り離した? → パターン判定
手順2:何が一定か確認(電源あり→V一定、電源なし→Q一定)
手順3:該当する公式を選ぶ
手順4:計算して答える
この4ステップを守れば、誘電体問題は怖くありません!
🎯 試験本番での解き方のコツ
⚡ 5ステップ攻略法
- 問題文をよく読む:単体か複数か、直列か並列か確認
- 必要な公式を書き出す:C=εS/d、直列・並列の式など
- 誘電体の有無を確認:εᵣが関係するか判断
- 数値を代入:単位に注意(μF、pFなど)
- 検算:並列なら増える、直列なら減る、で確認
⚠️ よくあるミス
❌ C=εS/dで、dを分子に書いてしまう(dは分母!)
❌ 直列・並列の公式を逆に使う
❌ 誘電体挿入で、電源の有無を確認せず計算
❌ 単位変換ミス(μF、pF、nFの混在)
❌ ε₀とεᵣを混同する
✨ まとめ:コンデンサは得点源にできる!
お疲れさまでした!コンデンサの静電容量、理解できましたか?😊
📌 この記事の重要ポイント
- ✅ 静電容量の公式:C = εS / d(ε、Sは分子、dは分母)
- ✅ 並列接続:C = C₁ + C₂(足すだけ!)
- ✅ 直列接続:1/C = 1/C₁ + 1/C₂(逆数を足す)
- ✅ 誘電体挿入:C' = εᵣ × C(比誘電率倍になる)
- ✅ 電源の有無で変化する量が異なる(V一定 or Q一定)
コンデンサの問題は、公式を正しく覚えて、パターンを見極めれば確実に得点できる分野です。特に誘電体挿入問題は、「電源の有無」を確認するだけで解法が決まります。
過去問を5〜10問解けば、出題パターンが見えてきます。公式の導出過程を理解しておけば、応用問題にも対応できるようになります!💪
📌 関連記事
電験三種の勉強時間はどのくらい?|科目別の目安と効率的な学習法まとめコンデンサを含む「理論」科目の学習時間配分と効率的な勉強法を解説しています。全体像を把握して、合格への最短ルートを進みましょう!
🚀 次のステップ
この記事を読んだら、すぐに過去問で実践してみましょう!
C=εS/dの公式と、直列・並列の計算を何度も練習することで、
試験本番でもスラスラ解けるようになります。
あなたの合格を心から応援しています!✨
📌 合わせて読みたい
独学で電気主任技術者3種合格への最強最短ルート:過去問から始める爆速勉強術コンデンサの問題も、過去問演習が最強の勉強法です。この記事で効率的な学習ロードマップを確認しましょう。