目次
⚡ こんな悩みを解決します
- ✅ 静電エネルギーの公式が3つもあって覚えられない
- ✅ どの公式を使えばいいのか判断できない
- ✅ なぜ「1/2」がつくのか理解できない
- ✅ コンデンサ接続でエネルギーが減る理由がわからない
📖 この記事を読むとわかること
- 静電エネルギーとは何か?(バネのイメージで理解)
- W = 1/2QV = 1/2CV² = 1/2Q²/C の使い分け方
- 問題文を見て瞬時に使う公式を選ぶコツ
- エネルギー保存則と仕事の関係
- コンデンサ接続時のエネルギー損失の正体
静電エネルギーは、電験三種で確実に得点できる分野です。公式の使い分けさえマスターすれば、計算問題はパターン化されています。この記事で完璧にしましょう!💡
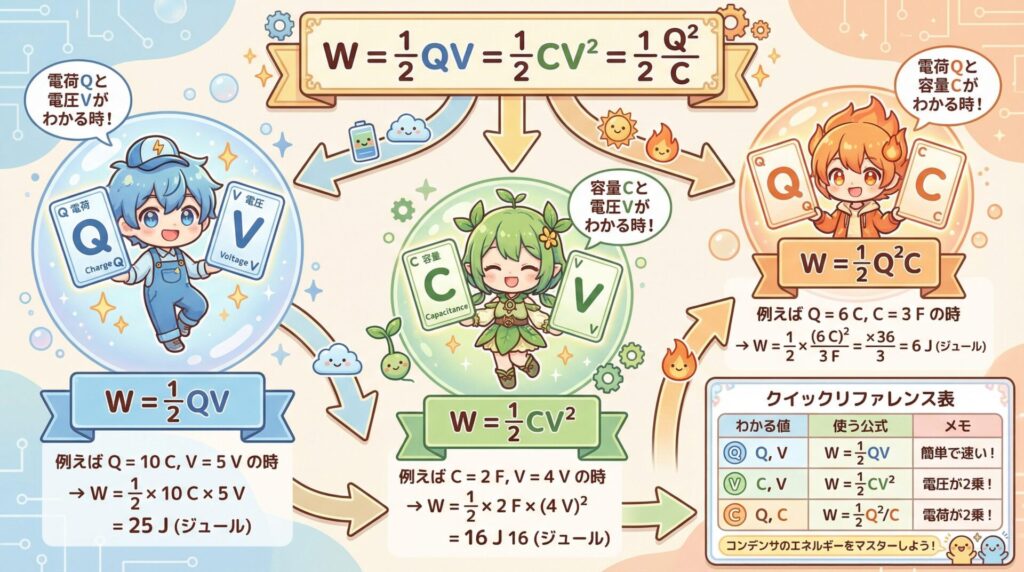
🎯 3つの公式の使い分け方
📊 使い分けの判断フローチャート
問題文を読んだら、「何が与えられているか?」を確認するだけ!
| 問題文に書いてあること | 使う公式 | 理由 |
|---|---|---|
| 電荷Q と 電圧V | W = 1/2 QV | そのまま代入できる |
| 静電容量C と 電圧V | W = 1/2 CV² | 最も頻出! |
| 電荷Q と 静電容量C | W = 1/2 Q²/C | 電圧Vが不明なとき |
💡 簡単な覚え方
「与えられている2つの文字を公式に当てはめる」
• Q と V がある → W = 1/2 QV
• C と V がある → W = 1/2 CV²
• Q と C がある → W = 1/2 Q²/C
これだけ!シンプルですよね?
💡 例題で実践:公式①
【例題1】電荷Q = 10μC、電圧V = 100Vのコンデンサの静電エネルギーを求めよ。
【解答】
ステップ1:何が与えられている? → Q と V
ステップ2:使う公式 → W = 1/2 × Q × V
ステップ3:計算
W = 1/2 × 10×10⁻⁶ × 100 = 1/2 × 10⁻³ = 5×10⁻⁴ J = 0.5mJ
答え:0.5mJ
💡 例題で実践:公式②
【例題2】静電容量C = 100μF、電圧V = 200Vのコンデンサの静電エネルギーを求めよ。
【解答】
ステップ1:何が与えられている? → C と V
ステップ2:使う公式 → W = 1/2 × C × V²
ステップ3:計算
W = 1/2 × 100×10⁻⁶ × 200² = 1/2 × 100×10⁻⁶ × 40000
= 1/2 × 4 = 2J
答え:2J
💡 例題で実践:公式③
【例題3】電荷Q = 20μC、静電容量C = 50μFのコンデンサの静電エネルギーを求めよ。
【解答】
ステップ1:何が与えられている? → Q と C
ステップ2:使う公式 → W = 1/2 × Q² / C
ステップ3:計算
W = 1/2 × (20×10⁻⁶)² / (50×10⁻⁶)
= 1/2 × (400×10⁻¹²) / (50×10⁻⁶) = 1/2 × 8×10⁻⁶
= 4×10⁻⁶ J = 4μJ
答え:4μJ
🎯 計算のコツ
• 単位に注意!μF、μCは10⁻⁶をつける
• V²は先に計算してから掛ける(200² = 40000)
• 1/2は最後に掛ける方が楽
• 指数計算は慎重に(10⁻⁶ × 10⁻⁶ = 10⁻¹²)
⚡ エネルギー保存則と仕事の関係
📚 エネルギー保存則とは?
物理学の最も基本的な法則の一つがエネルギー保存則です。
エネルギー保存則
「エネルギーの総量は変わらない」
コンデンサの場合も同じです:
⚡ 充電のとき:
電源が行った仕事 = コンデンサに蓄えられたエネルギー
⚡ 放電のとき:
コンデンサに蓄えられたエネルギー = 外部に放出される仕事
🔄 仕事とエネルギーの関係
「仕事」と「エネルギー」は、実は同じものです!
| 状況 | エネルギーの流れ |
|---|---|
| 充電中 | 電源の電気エネルギー → コンデンサの静電エネルギー |
| 放電中 | コンデンサの静電エネルギー → 抵抗での熱エネルギー |
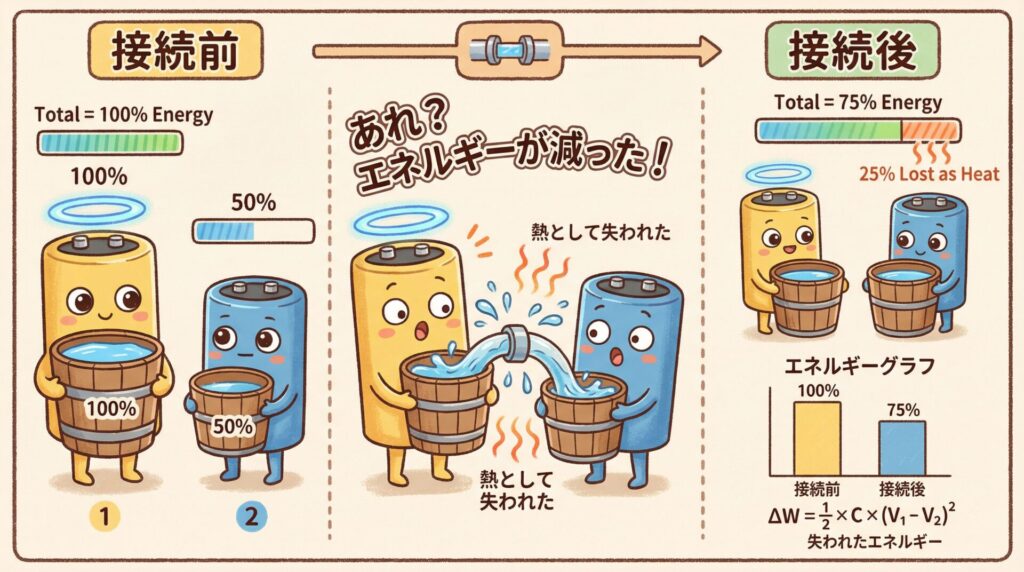
💥 コンデンサ接続時のエネルギー損失
😱 不思議な現象:エネルギーが減る!
電験三種で頻出なのが、異なる電圧のコンデンサ同士を接続する問題です。このとき、驚くべきことが起きます!
⚠️ 衝撃の事実
電荷は保存されるのに、
エネルギーは必ず減少する!
🤔 なぜエネルギーが減るのか?
💡 水タンクで理解する
高い位置の水(高電圧のコンデンサ)と低い位置の水(低電圧のコンデンサ)を繋ぐと:
- 水が高い方から低い方へ流れる(電荷の移動)
- 最終的に両方の水位が同じになる(電圧が等しくなる)
- でも、水が流れるとき「ザバーン!」と波打ってエネルギーが失われる
コンデンサでも同じ!接続時に電荷が移動する過程で、導線の抵抗で熱として失われます。
📐 エネルギー損失の計算
コンデンサ接続時のエネルギー損失を計算するパターンを見ていきましょう。
エネルギー損失の計算手順
ステップ1:接続前の総エネルギーW₁を計算
W₁ = コンデンサ1のエネルギー + コンデンサ2のエネルギー
ステップ2:接続後の電圧V'を求める
電荷保存則:Q₁ + Q₂ = (C₁ + C₂) × V'
→ V' = (Q₁ + Q₂) / (C₁ + C₂)
ステップ3:接続後の総エネルギーW₂を計算
W₂ = 1/2 × (C₁ + C₂) × V'²
ステップ4:エネルギー損失ΔWを計算
ΔW = W₁ − W₂
💡 例題で実践:エネルギー損失
【例題】C₁ = 2μF、V₁ = 100V のコンデンサと、C₂ = 3μF、V₂ = 50V のコンデンサを並列接続した。エネルギー損失を求めよ。
【解答】
ステップ1:接続前の総エネルギー
W₁ = 1/2 × C₁ × V₁² + 1/2 × C₂ × V₂²
= 1/2 × 2×10⁻⁶ × 100² + 1/2 × 3×10⁻⁶ × 50²
= 1/2 × 2×10⁻⁶ × 10000 + 1/2 × 3×10⁻⁶ × 2500
= 10⁻² + 3.75×10⁻³ = 0.01 + 0.00375 = 0.01375 J
ステップ2:接続後の電圧(電荷保存則より)
Q₁ = C₁ × V₁ = 2×10⁻⁶ × 100 = 2×10⁻⁴ C
Q₂ = C₂ × V₂ = 3×10⁻⁶ × 50 = 1.5×10⁻⁴ C
V' = (Q₁ + Q₂) / (C₁ + C₂) = (2×10⁻⁴ + 1.5×10⁻⁴) / (5×10⁻⁶)
= 3.5×10⁻⁴ / 5×10⁻⁶ = 70 V
ステップ3:接続後の総エネルギー
W₂ = 1/2 × (C₁ + C₂) × V'²
= 1/2 × 5×10⁻⁶ × 70² = 1/2 × 5×10⁻⁶ × 4900
= 0.01225 J
ステップ4:エネルギー損失
ΔW = W₁ − W₂ = 0.01375 − 0.01225
= 0.0015 J = 1.5mJ
答え:1.5mJ が熱として失われる
🎯 重要ポイント
✅ 電荷は保存される(Q₁ + Q₂ = Q')
✅ エネルギーは必ず減少する(W₁ > W₂)
✅ 損失分は熱エネルギーに変換される
✅ 電圧が等しいコンデンサを接続 → 損失ゼロ
✨ まとめ:静電エネルギーは得点源!
お疲れさまでした!静電エネルギー、理解できましたか?😊
📌 この記事の重要ポイント
- ✅ 静電エネルギーには必ず「1/2」がつく
- ✅ 3つの公式:W = 1/2QV = 1/2CV² = 1/2Q²/C
- ✅ 与えられている2つの文字で公式を選ぶ
- ✅ エネルギーと仕事は同じもの
- ✅ コンデンサ接続時はエネルギーが必ず減少する
静電エネルギーの問題は、公式の使い分けさえマスターすれば確実に得点できる分野です。「何が与えられているか?」を見るだけで、使う公式が決まります。
特にコンデンサ接続問題は頻出です。「電荷は保存、エネルギーは減少」というパターンを覚えておけば、どんな問題でも対応できます!💪
⚠️ よくあるミス
❌ 1/2を忘れる(答えが2倍になる)
❌ V²を計算せずにVのまま使う
❌ 単位変換ミス(μF、μCの10⁻⁶を忘れる)
❌ 接続前後でエネルギーが増えたと計算してしまう
❌ 公式を覚えようとして混乱する(与えられた文字で選ぶだけ!)
🚀 次のステップ
この記事を読んだら、すぐに過去問で実践してみましょう!
「与えられている文字を探す」→「公式に当てはめる」
この2ステップで解けることを実感してください。
あなたの合格を心から応援しています!✨