目次
💡 この記事で解決できる悩み
- 「誘電体って何?絶縁体と何が違うの?」
- 「比誘電率εᵣと誘電率εの違いがわからない…」
- 「分極現象って、何が起こってるの?」
- 「公式 ε = εᵣ × ε₀ の意味を理解したい!」
✅ この記事を読めば、「サンドイッチ」と「水に浮かぶ葉っぱ」の例えで、誘電体の仕組みが目に見えるように理解できます!
静かに充実した生活を送る
目次
✅ この記事を読めば、「サンドイッチ」と「水に浮かぶ葉っぱ」の例えで、誘電体の仕組みが目に見えるように理解できます!
こんにちは!電験三種の「理論」科目で、初心者が「なんとなく」で済ませがちなのが誘電体です。
「コンデンサの間に挟まれてる物質でしょ?」と軽く考えていると、比誘電率εᵣの計算問題で撃沈します。でも、本質を理解すれば、実は簡単な単元なんです!
結論から言うと、誘電体は「コンデンサの容量を増やす魔法の物質」です。そして、その魔法の正体が分極現象なんですね。
📌 この記事のゴール
まず、誘電体(ゆうでんたい)とは何なのか、基本から確認しましょう。
誘電体は、コンデンサの2枚の金属板の間に挟まれる絶縁体のことです。「絶縁体なら何でもいいの?」と思うかもしれませんが、実は誘電体には特別な効果があるんです。
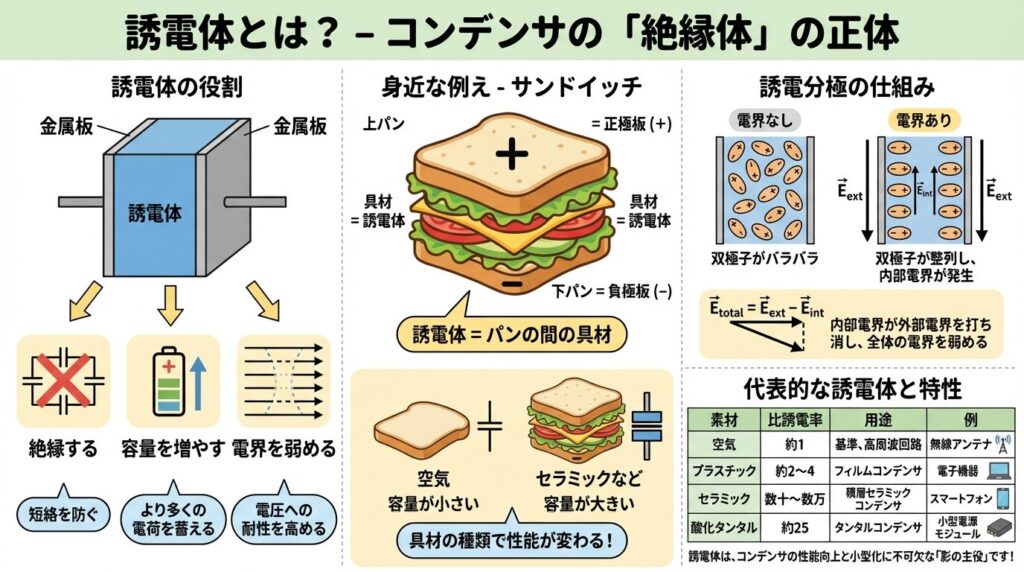
誘電体を理解する一番簡単な方法は、「サンドイッチ」に例えることです。
🥪 サンドイッチの例え
・上のパン → プラス(+)の金属板
・下のパン → マイナス(-)の金属板
・間の具材 → 誘電体
具材(誘電体)の種類を変えると、サンドイッチ(コンデンサ)の性能が変わります!
誘電体には、以下の3つの重要な役割があります。
| 役割 | 効果 | 例え |
|---|---|---|
| ① 絶縁する | 金属板同士が接触してショートするのを防ぐ | パンの間に具材があるから崩れない |
| ② 容量を増やす | コンデンサの静電容量Cを大きくする | 具材が多いとボリューム満点! |
| ③ 電界を弱める | 金属板間の電界の強さEを小さくする | 具材がクッションになる |
この中で、電験三種で特に重要なのが②容量を増やす効果です。この効果を数値化したものが比誘電率εᵣなんです!
ここが初心者が混乱しやすいポイントです。誘電率εと比誘電率εᵣは違うものなんです!
つまり、誘電率εは、比誘電率εᵣと真空の誘電率ε₀の掛け算で求まります。
💡 比誘電率εᵣの意味
比誘電率εᵣは、「真空に比べて何倍か」を表す数字です。
・真空(または空気) → εᵣ = 1.0
・紙 → εᵣ ≈ 2〜4
・ガラス → εᵣ ≈ 5〜10
・セラミック → εᵣ ≈ 10〜10000
つまり、εᵣが大きいほど、容量が増える!
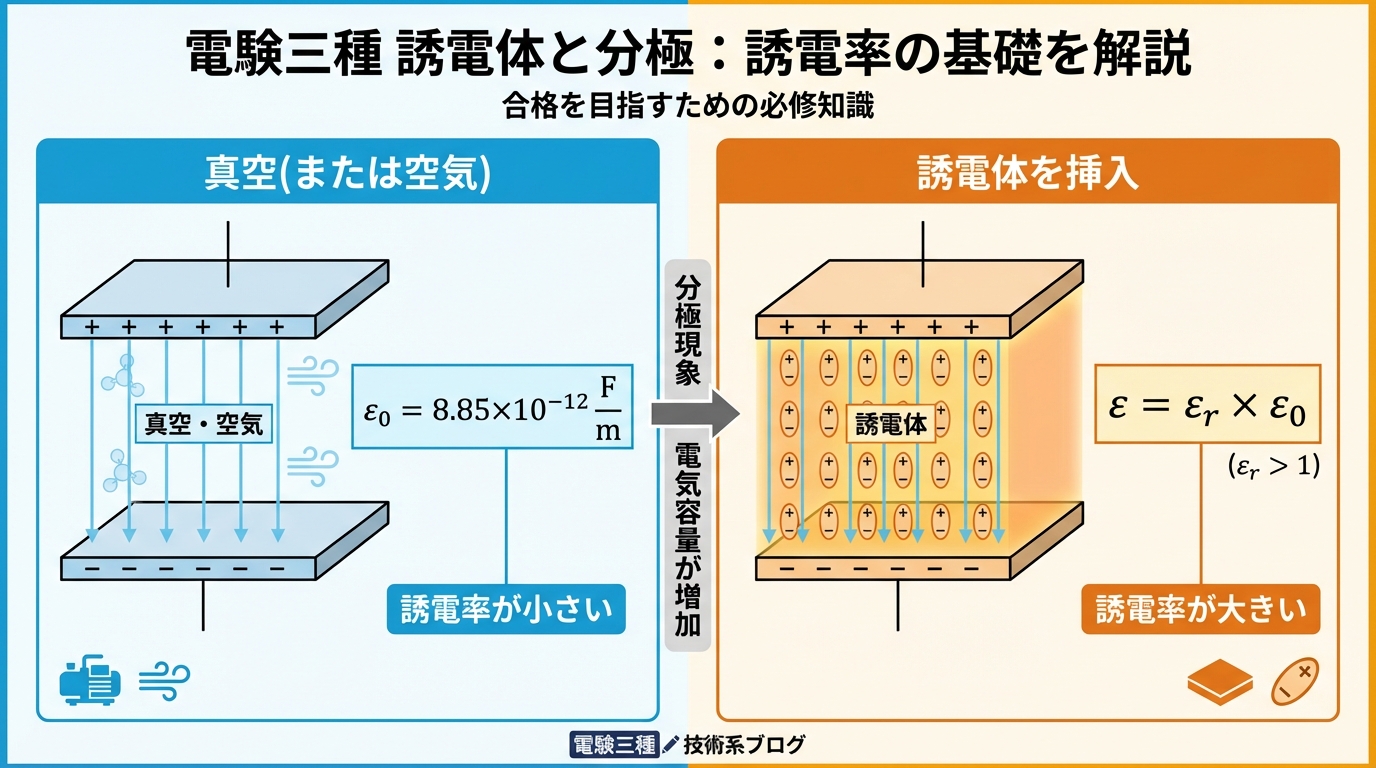
誘電体を入れると、コンデンサの容量がεᵣ倍に増えます。公式で表すとこうなります。
真空中の容量:
C₀ = ε₀S/d
誘電体を挿入した容量:
C = εS/d = εᵣ × ε₀S/d = εᵣ × C₀
つまり:
誘電体を入れると、容量がεᵣ倍になる!
でも、なぜこんなことが起こるのでしょうか?その秘密が分極現象です。
ここからが誘電体の一番面白いところです!分極現象を理解すれば、誘電体の謎がすべて解けます。
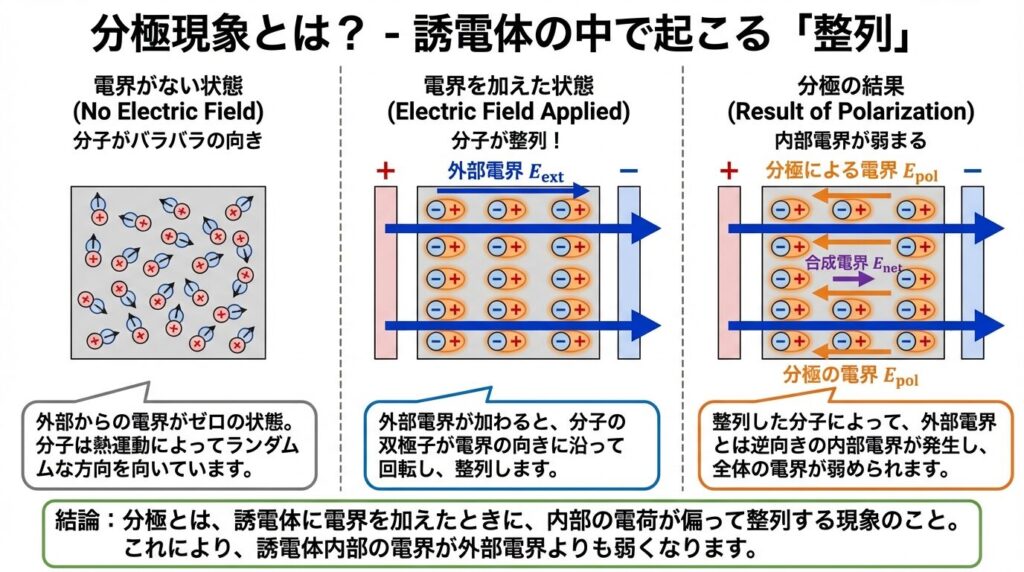
分極現象とは、電界をかけると、誘電体の中の分子が整列する現象です。この「整列」が、容量を増やす正体なんですね。
分極現象を理解する一番簡単な方法は、「水に浮かぶ葉っぱ」の例えです。
🍃 水に浮かぶ葉っぱの例え
【電界がないとき】
池に浮かぶ葉っぱは、バラバラの向きを向いています。
→ これが分極していない状態
【電界をかけたとき】
水流(電界)が流れると、葉っぱが一斉に流れの向きに整列します!
→ これが分極した状態
水流 = 電界、葉っぱ = 誘電体の分子
もう少し詳しく見ていきましょう。誘電体の分子は、実は小さな磁石のようなものです。
Step 1: 電界がない状態
分子(小さな磁石)がバラバラの向きを向いている
→ プラスとマイナスが打ち消し合って、全体として中性
Step 2: 電界をかける
金属板に電圧をかけると、電界Eが発生
→ 分子が電界の向きに引っ張られる
Step 3: 分子が整列(分極)
すべての分子のプラス側が一方向、マイナス側が逆方向に整列!
→ これが分極現象
ここが重要です!分極が起こると、電界が弱くなります。
なぜ電界が弱くなる?
分極した分子は、元の電界と逆向きの電界を作ります。
元の電界(金属板が作る) - 分極の電界(分子が作る)
= 実際の電界(弱くなる!)
公式で表すと:
E = E₀ / εᵣ
電界が弱くなる → 同じ電圧でもっと電気量を蓄えられる → 容量が増える!
これが、誘電体を入れると容量が増える仕組みです。分極現象が「魔法の正体」だったんですね。
実は、分極には3つの種類があります。電験三種では詳しく問われませんが、知っておくと理解が深まります。
| 種類 | メカニズム | 例 |
|---|---|---|
| 電子分極 | 電子雲が原子核からずれる | ほとんどの物質 |
| イオン分極 | イオン結晶内でイオンがずれる | 食塩(NaCl) |
| 配向分極 | 分子全体が回転して整列 | 水(H₂O) |
🔑 ポイント
試験では種類まで問われることはほぼありません。「分極 = 分子の整列」というイメージだけ掴んでおけばOKです!
ここからは、実際の試験で出題される計算問題を攻略していきましょう!
誘電体の計算問題は、パターンが決まっています。公式をしっかり押さえれば、確実に得点できます!
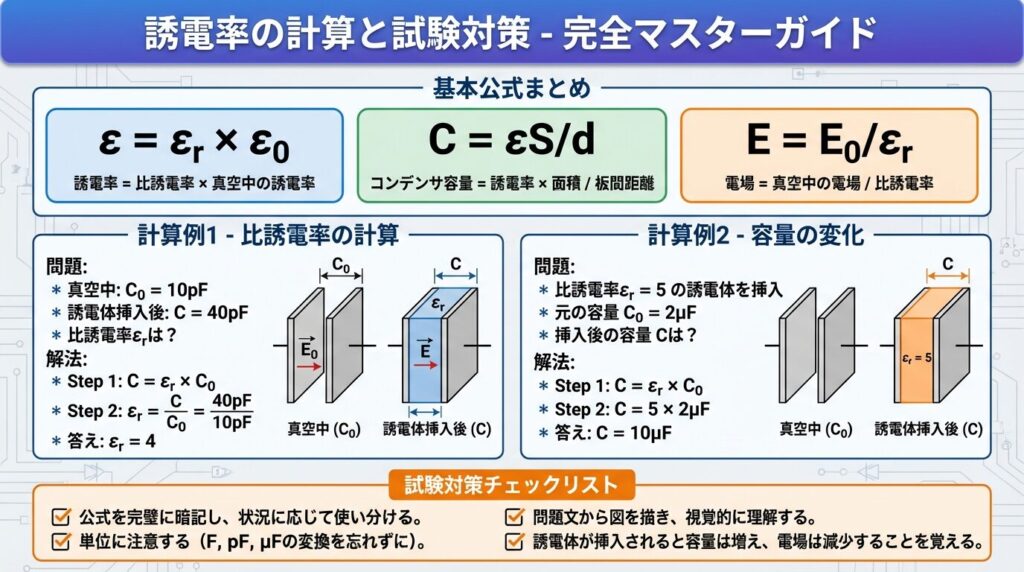
まず、誘電体に関する3つの基本公式を押さえましょう。この3つだけ覚えれば、ほとんどの問題が解けます!
【問題】
真空中のコンデンサの容量C₀ = 10pF。誘電体を挿入すると容量C = 40pFになった。比誘電率εᵣは?
【解答】
公式 C = εᵣ × C₀ を使う
40 = εᵣ × 10
εᵣ = 40 ÷ 10
εᵣ = 4
✅ 確認: 容量が4倍になったので、比誘電率も4です!
【問題】
真空中の電界E₀ = 1000 V/m。比誘電率εᵣ = 5の誘電体を挿入すると、電界Eは?
【解答】
公式 E = E₀ / εᵣ を使う
E = 1000 ÷ 5
E = 200 V/m
✅ 確認: 電界が1/5に弱くなりました!
試験で使う数値は、これだけ覚えておけばOKです!
| 物質 | 比誘電率εᵣ | 覚え方 |
|---|---|---|
| 真空 | 1.0(基準) | すべての基準 |
| 空気 | ≈ 1.0 | 真空とほぼ同じ |
| 紙 | 2〜4 | 2倍〜4倍 |
| ガラス | 5〜10 | 5倍〜10倍 |
| ε₀(真空の誘電率) | 8.85×10⁻¹² F/m | 定数として暗記! |
🎯 試験頻出パターン
✅ 誘電体とは = コンデンサの間に挟まれる「絶縁体」
→ サンドイッチの「具材」のイメージ
✅ 3つの役割 = 絶縁、容量UP、電界を弱める
✅ 比誘電率εᵣ = 「真空に比べて何倍か」を表す数値
→ εᵣが大きいほど容量が増える
✅ 分極現象 = 分子が整列する現象
→ 「水に浮かぶ葉っぱ」のイメージ
✅ 基本公式3つ
① ε = εᵣ × ε₀
② C = εᵣ × C₀
③ E = E₀ / εᵣ
🎓 合格への学習法
1. イメージで覚える
→ サンドイッチ、水に浮かぶ葉っぱの例えを頭に思い浮かべる
2. 公式は3つだけ
→ ε = εᵣ × ε₀、C = εᵣ × C₀、E = E₀ / εᵣ
3. εᵣとε₀を混同しない
→ εᵣは無次元(単位なし)、ε₀は定数(8.85×10⁻¹² F/m)
4. 過去問を5問解く
→ パターンは3種類だけ。すぐに慣れます!
🔗 関連記事で理解を深めよう!
この記事を読んだあなたは、もう誘電体で迷うことはありません。
「サンドイッチ」と「水に浮かぶ葉っぱ」のイメージを思い出しながら、問題を解いてみてください!
電験三種合格、心から応援しています!🎓