📚 こんな疑問、ありませんか?
- 「有限母集団補正」ってそもそも何?
- なぜ母集団が小さいとサンプルサイズが減るの?
- 式を見ても、なぜその形になるのかピンとこない…
- QC検定の問題で計算はできるけど、本質がわからない
✅ この記事でわかること
- 有限母集団補正の「直感的な意味」をカゴとボールで理解
- なぜ補正すると小さくなるのかを数式なしで把握
- 式の意味を「残りの割合」で納得
- 実際の計算問題の解き方をステップで習得
統計学の問題を解いていると、突然登場する「有限母集団補正」。
「なんか式を掛けるとサンプルサイズが小さくなるらしい」とは知っていても、なぜそうなるのかがモヤモヤしていませんか?
実は、この補正の考え方は「カゴの中のボールを取り出すイメージ」で驚くほどスッキリ理解できます。
この記事では、数式を暗記するのではなく、「なぜその式になるのか」を徹底的にイメージで解説します。最後には添付の問題も一緒に解いていきましょう!
📖 関連記事
▶ 抜取検査の基本|全数検査との違いをイメージで理解
目次
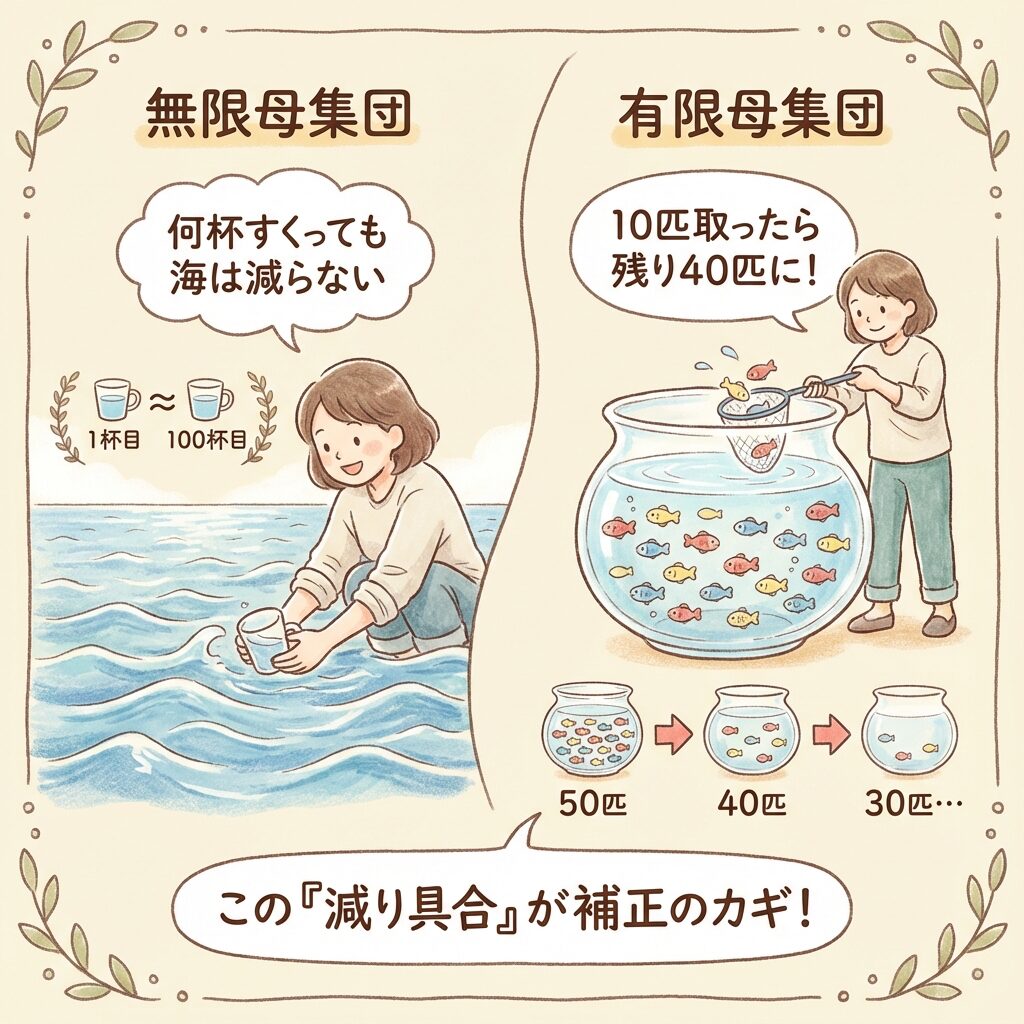
🎯 そもそも「無限母集団」と「有限母集団」って何?
まず、サンプリング(抜き取り検査)の世界には2つの「母集団」があります。
💡 無限母集団のイメージ:海の水
無限母集団とは、「取っても取っても減らない」と考えられるほど大きな集団のことです。
たとえば、海の水をコップ1杯すくっても、海の水はほとんど減りませんよね?
🌊 コップ1杯目も、100杯目も、海の状態はほぼ同じ
💡 有限母集団のイメージ:金魚すくいの水槽
有限母集団とは、「取ると明らかに減る」とわかる大きさの集団です。
たとえば、金魚すくいの水槽に50匹の金魚がいるとします。
10匹すくったら、残りは40匹。次にすくうとき、状況が明らかに変わっているんです。
🐟 取れば取るほど、残りが減っていく → これが有限母集団
📊 無限母集団 vs 有限母集団の違い
| 項目 | 無限母集団 | 有限母集団 |
|---|---|---|
| イメージ | 海、大きな倉庫 | 金魚鉢、小さな箱 |
| 取ったあと | ほとんど変わらない | 明らかに減る |
| 確率の変化 | ほぼ一定 | 取るたびに変わる |
| 補正の必要性 | 不要 | 必要! |
💡 超重要ポイント
有限母集団では、「取れば取るほど残りが減る」ので、同じ精度を得るのに必要なサンプルサイズが少なくて済むのです。これが補正の本質!
🔧 有限母集団補正係数の「意味」をイメージで理解
さて、ここからが本題です。有限母集団補正係数の式を見てみましょう。
有限母集団補正係数
√(N − n / N − 1)
N:母集団の大きさ n:サンプルサイズ
この式、パッと見ただけでは「なぜこうなるの?」と思いますよね。
でも大丈夫。「残りの割合」という視点で見ると、一気に納得できます。
🎁 箱の中のプレゼントで考えてみよう
50個のプレゼントが入った箱があります(N = 50)。
この中から10個を取り出して中身を確認します(n = 10)。
10個取ったあと、箱には何個残っていますか?
📦 50 − 10 = 40個 残っている!
📐 式の分子「N − n」の意味
式の分子「N − n」は、まさにこの「残りの数」を表しています。
上の例なら:50 − 10 = 40
つまり、「まだ調べていない部分がどれだけあるか」ということですね。
📐 式の分母「N − 1」の意味
分母の「N − 1」は、「最初から1個取った状態で、残りがどれだけか」を表します。
なぜ「N」ではなく「N − 1」なのか?これは統計学で「不偏推定」という考え方に関係しています(標本分散でも「n − 1」で割りますよね)。
💡 ざっくり言うと、「サンプリングを始めた時点で1個分の情報は確定する」という考え方です。
🧮 補正係数を計算してみよう
例:N = 50、n = 10 の場合
① 分子を計算:50 − 10 = 40
② 分母を計算:50 − 1 = 49
③ 割り算:40 ÷ 49 = 0.816...
④ 平方根を取る:√0.816 = 約 0.903
→ 補正係数は約 0.9(1より小さい!)
💡 ここがポイント!
補正係数は必ず1以下になります。だから、これを分散に掛けると分散が小さくなり、結果として必要なサンプルサイズも小さくなるのです!
📖 関連記事
▶ サンプリングの基本と抜取検査の考え方
🤔 なぜ補正すると「必要なサンプル数」が減るの?
これが最も重要な「なぜ」です。直感的に理解しましょう。
🎰 くじ引きで考える「情報の価値」
【ケース1】1000本のくじから10本を引く
あなたは1000本のくじが入った箱から、10本を引きました。
残り990本は、まだ何が入っているかわかりません。
→ 引いた10本の情報だけでは、全体のことはあまりわからない…
【ケース2】50本のくじから10本を引く
今度は50本しかない箱から、同じく10本を引きました。
残り40本。全体の20%を調べたことになります!
→ 同じ10本でも、全体に対する「情報量」が圧倒的に大きい!
N = 1000 から n = 10
1%
を調べただけ
N = 50 から n = 10
20%
を調べた!
💎 核心:「同じ精度」を得るのに必要な数が減る
無限母集団(海の水)では、コップ100杯すくっても、海のことはほんの少ししかわかりません。
でも有限母集団(金魚鉢)では、10匹調べたら全体の20%がわかります。
→ だから、同じ精度(信頼度)を得るために、より少ないサンプルで済むのです!
🎯 極端な例:全部調べたらどうなる?
N = 50 で、n = 50(全部調べる)の場合、補正係数はどうなるでしょう?
分子:50 − 50 = 0
計算:√(0 / 49) = 0
→ 分散が0になる = 誤差ゼロ = 完全に全部わかった!
これは当然ですよね。全部調べたらサンプリング誤差なんてないわけですから。
有限母集団補正は、この「全部調べれば誤差ゼロ」という常識を数式で表現しているのです。
📖 もっと詳しく学ぶ
▶ 信頼区間とサンプルサイズの関係を図解
✏️ 添付問題を一緒に解いてみよう!
【問題】
無限母集団から単純ランダムサンプリングでn個のサンプルを抽出するとき、
母平均を信頼率95%で幅±eの範囲に推定するためのサンプルサイズはn = 100であった。
大きさN = 300の有限母集団から同じ精度で推定するのに必要なサンプルサイズは?
📝 解き方の流れ
💡 ポイント:有限母集団では補正を使う!
Step 1:有限母集団のサンプルサイズ n' を求める公式を確認
n' = (n × N) / (n + N − 1)
n:無限母集団での必要サンプルサイズ
N:有限母集団の大きさ
n':有限母集団での必要サンプルサイズ
Step 2:数値を代入
n = 100、N = 300 を代入すると:
n' = (100 × 300) / (100 + 300 − 1)
n' = 30000 / 399
n' = 75.19...
Step 3:切り上げて整数に
サンプルサイズは整数なので、切り上げてn' = 76
✅ 答え
n' = 76
無限母集団で100個必要だったのが、76個で済む!
🔍 なぜこの公式になるの?
この公式は、先ほどの補正係数から導かれます。
無限母集団での分散の推定精度を、有限母集団でも同じにするために補正係数を使うと、
数式を変形していくとこの形にまとまるのです。
💡 覚え方:分子は「n × N」の掛け算、分母は「n + N − 1」の足し算
📌 まとめ:有限母集団補正の本質
- 無限母集団:取っても減らない → 補正不要
- 有限母集団:取れば減る → 同じ精度なら少ないサンプルでOK
- 補正係数 √((N−n)/(N−1)):「残りの割合」を表す
- 補正係数は必ず1以下なので、分散が小さくなる
- サンプルサイズの公式:n' = (n × N) / (n + N − 1)
📚 キーワード解説一覧(QC検定対策)
| 用語 | 意味・ポイント |
|---|---|
| 無限母集団 | サンプリングしても「減った」と考えなくてよいほど大きな集団。工程から連続的に生産される製品などが該当。 |
| 有限母集団 | 大きさが有限で、サンプリングすると「残り」が明確に減る集団。ロット検査などが該当。 |
| 有限母集団補正(FPC) | Finite Population Correction。有限母集団からサンプリングする際に、標準誤差を小さくする補正。 |
| 補正係数 | √((N−n)/(N−1))。分散または標準誤差に掛ける係数で、常に1以下の値になる。 |
| サンプリング比 | n/N。母集団に対するサンプルの割合。これが5%以下なら補正を省略できることが多い。 |
| 単純ランダムサンプリング | 母集団のすべての要素が等確率で選ばれるサンプリング方法。無作為抽出とも呼ぶ。 |
| 復元抽出・非復元抽出 | 復元抽出は取ったものを戻す方法(無限母集団扱い)。非復元抽出は戻さない方法(有限母集団補正が必要)。 |
⚠️ 試験での注意点
QC検定では「サンプリング比(n/N)が5%以下なら補正不要」というルールがよく出題されます。問題文をよく読んで、補正が必要かどうかを判断しましょう!
📖 次に読むべき記事

