- 「分散分析表って何?どうやって作るの?」
- 「自由度の決め方がわからない…」
- 「平均平方とF値って何を計算しているの?」
- 分散分析表の役割と構造
- 自由度の決め方(なぜその数になるのか)
- 平均平方の計算方法
- F値の意味と計算
- 具体例で表を完成させる全手順
前回の記事で、平方和(ST, SR, Se)の計算方法を学びました。
今回は、その平方和を使って「分散分析表」を完成させます。
分散分析表を作れば、「この重回帰式は本当に使えるのか?」を統計的に判断できるようになります。
【計算例あり】重回帰の平方和の分解|SR, Se, ST の意味と求め方 →
目次
📊 分散分析表とは?
分散分析表(ANOVA表)は、「バラつきを要因ごとに整理した表」です。
「回帰によるバラつき」と「残差(誤差)によるバラつき」を比較して、
回帰モデルが統計的に意味があるかどうかを判定する
📋 分散分析表の構造
重回帰分析の分散分析表は、以下のような形をしています。
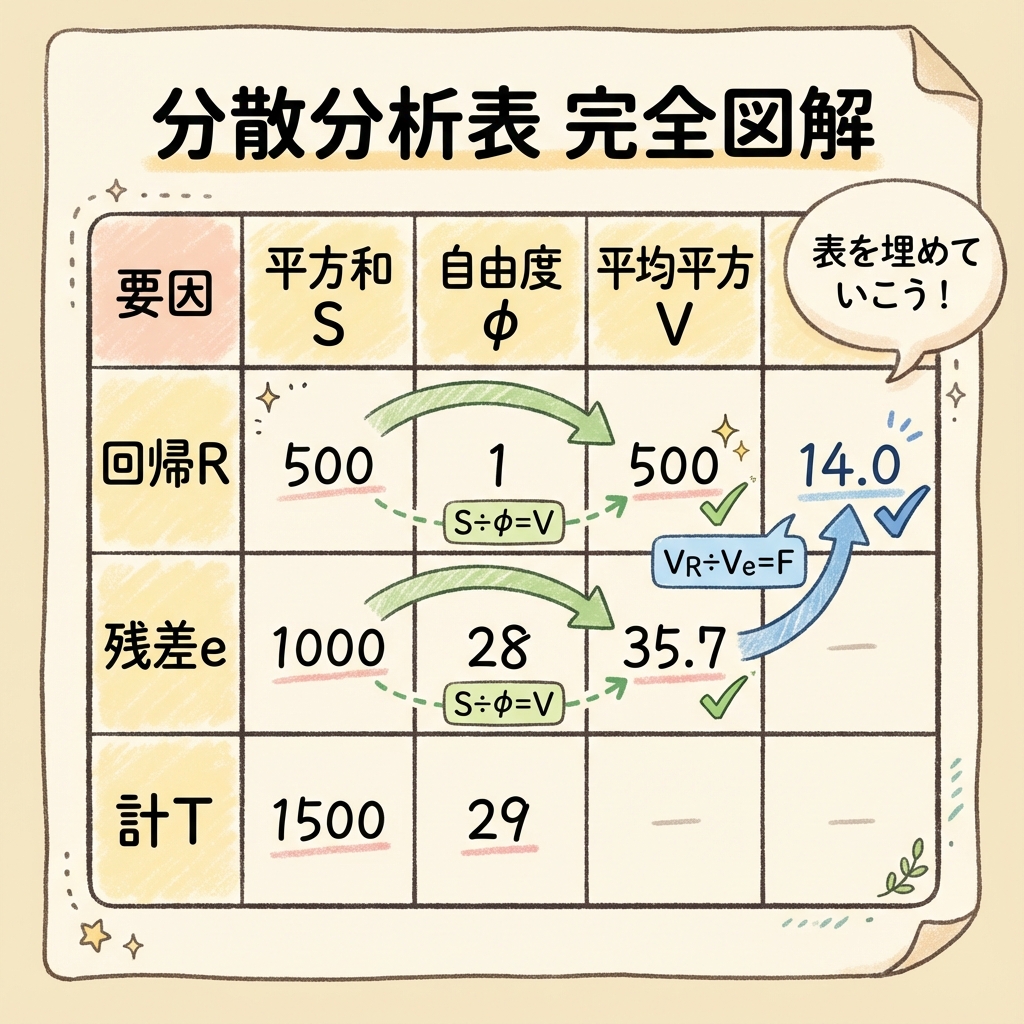
| 要因 | 平方和 S | 自由度 φ | 平均平方 V | F値 F₀ |
|---|---|---|---|---|
| 回帰 R | SR | φR | VR | F₀ |
| 残差 e | Se | φe | Ve | − |
| 計 T | ST | φT | − | − |
🔤 各列の意味
| 列 | 記号 | 意味 |
|---|---|---|
| 平方和 | S | バラつきの大きさ(前回計算済み) |
| 自由度 | φ(ファイ) | 自由に動けるデータの数 |
| 平均平方 | V | 1自由度あたりのバラつき(= S ÷ φ) |
| F値 | F₀ | 回帰と残差のバラつきの比(= VR ÷ Ve) |
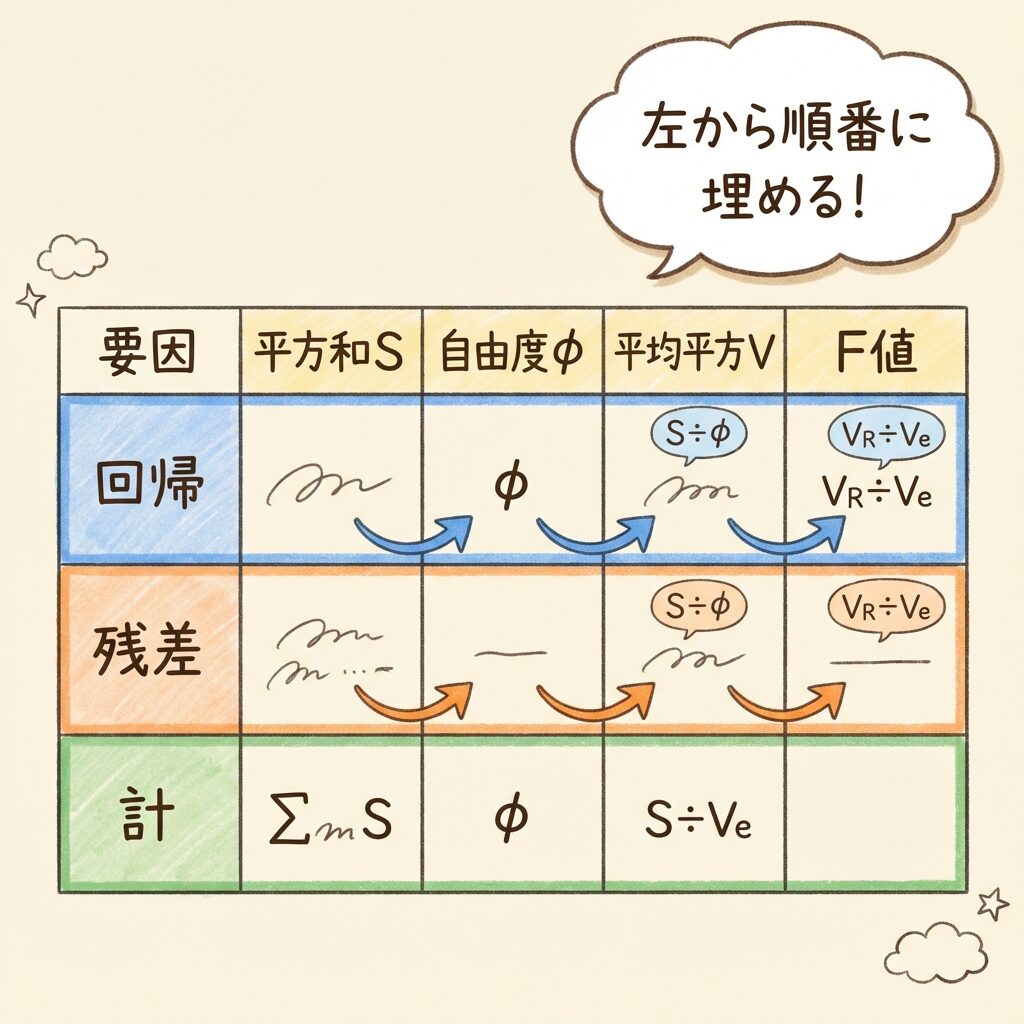
S(平方和)→ φ(自由度)→ V(平均平方)→ F₀(F値)
左から右へ順番に埋めていけば、表が完成します。
分散分析表の作り方|表を完成させる手順 →
🎯 自由度の決め方
分散分析表で最も「なぜ?」と思うのが自由度ではないでしょうか。
でも、ルールを覚えれば簡単です。
📐 重回帰分析の自由度公式
|
φT(総)
n − 1 |
= |
φR(回帰)
k |
+ |
φe(残差)
n − k − 1 |
n = データ数、k = 説明変数の数
🤔 なぜこの数になるの?
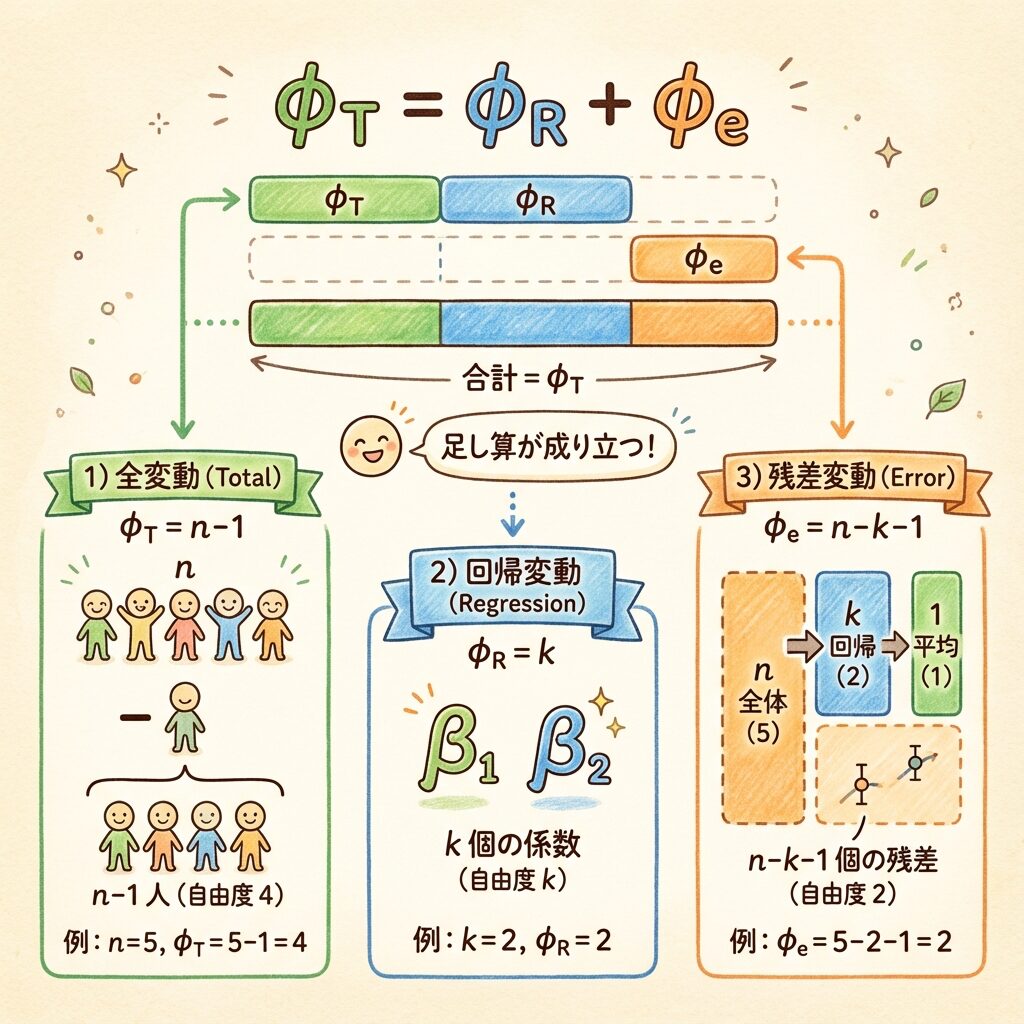
🟢 総自由度 φT = n − 1
データがn個あっても、平均を固定すると自由に動けるのは n−1 個です。
5人の合計点が100点と決まっていたら、4人の点数が決まれば最後の1人は自動的に決まりますよね。自由に決められるのは4人分(n−1)です。
🔵 回帰自由度 φR = k
回帰式で推定するパラメータ(偏回帰係数)の数です。説明変数がk個なら、β₁, β₂, ..., βk の k 個を推定します。
説明変数が2つ(x₁, x₂)なら、φR = 2 です。
🟠 残差自由度 φe = n − k − 1
「総自由度」から「回帰自由度」と「切片の分(1)」を引いた残りです。
φe = φT − φR = (n − 1) − k = n − k − 1
データがn個、推定するパラメータがk+1個(切片β₀ + 偏回帰係数k個)なので、残りは n − k − 1 個です。
【完全図解】自由度とは?|「なぜn-1で割るのか」を中学生でも分かるように解説 →
✅ 自由度の検算
自由度も平方和と同じく、足し算が成り立ちます。
(n − 1) = k + (n − k − 1) ✓
計算が合わなければ、どこかでミスしています。必ず検算しましょう。
📐 平均平方の計算
平均平方(V)は、「1自由度あたりのバラつき」です。
平均平方 = 平方和 ÷ 自由度
🤔 なぜ平均平方を計算するの?
平方和(S)だけでは、データ数や説明変数の数が違うと比較できないからです。
【例え:クラスの合計点】
| Aクラス(30人)の合計点 = 2400点 |
| Bクラス(20人)の合計点 = 1800点 |
どっちが優秀? → 人数で割って平均を出さないとわからない!
平均平方も同じです。自由度で割ることで、公平に比較できるようになります。
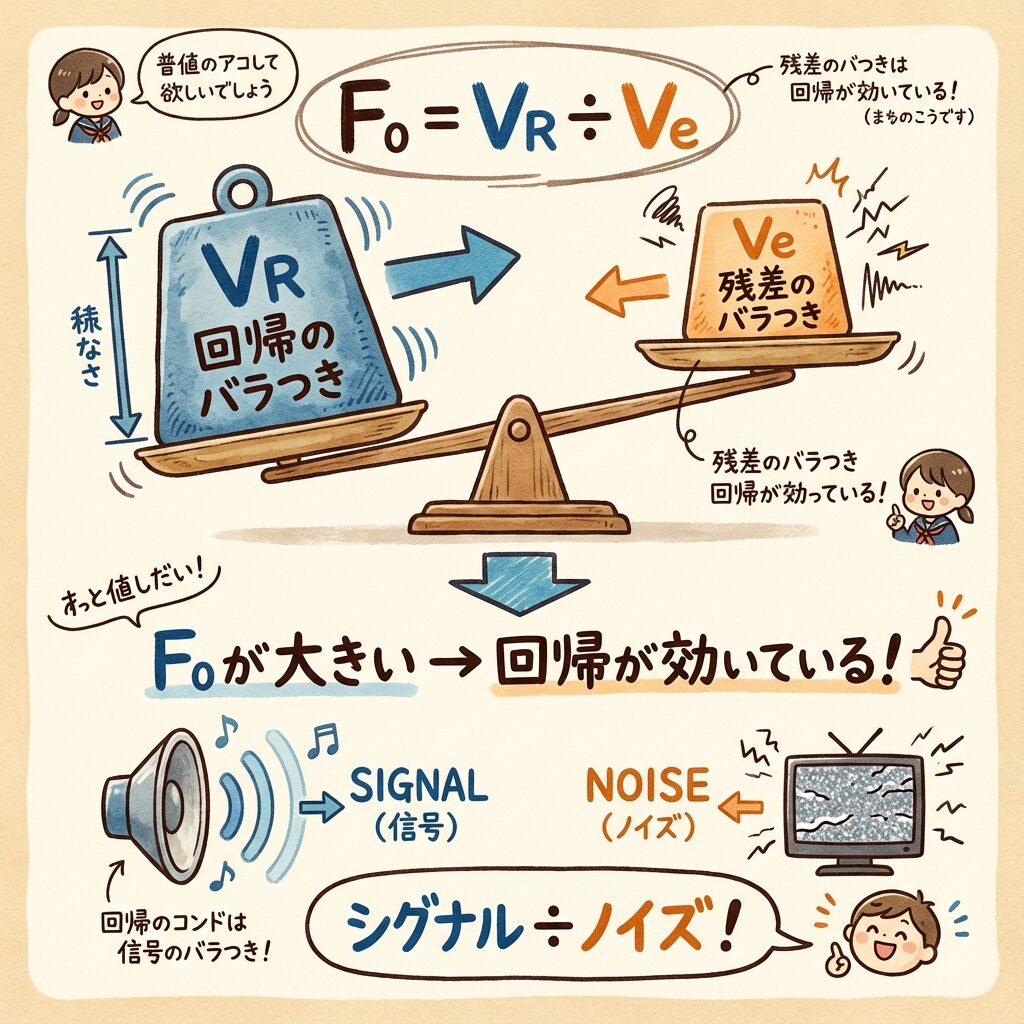
🔥 F値の計算と意味
F値は、「回帰のバラつき」と「残差のバラつき」を比較した比です。
🎯 F値の解釈
| F₀の値 | 意味 | 判定 |
|---|---|---|
| 大きい 📈 | 回帰による説明 > 残差(誤差) | 回帰モデルは有効 😊 |
| 1に近い | 回帰による説明 ≒ 残差(誤差) | 微妙… 🤔 |
| 小さい 📉 | 回帰による説明 < 残差(誤差) | 回帰モデルは無効 😢 |
F値は「シグナル(回帰)とノイズ(残差)の比」です。
シグナルがノイズより十分大きければ(F値が大きければ)、回帰モデルは「意味がある」と判断できます。
F検定で有意差を判定する|F分布表の使い方 →
F分布のイメージ|なぜ分散は「引き算」ではなく「割り算」で比べるのか? →
📊 具体例で分散分析表を完成させよう
前回の記事で計算した平方和を使って、分散分析表を完成させましょう。
📋 前回までの結果
- データ数:n = 5
- 説明変数の数:k = 2(温度 x₁、圧力 x₂)
- 総平方和:ST = 49.20
- 回帰平方和:SR = 48.93
- 残差平方和:Se = 0.27
🔢 Step 1:自由度を計算
| 自由度 | 公式 | 計算 | 結果 |
|---|---|---|---|
| φR(回帰) | k | 2 | 2 |
| φe(残差) | n − k − 1 | 5 − 2 − 1 | 2 |
| φT(総) | n − 1 | 5 − 1 | 4 |
検算:φR + φe = 2 + 2 = 4 = φT ✓
🔢 Step 2:平均平方を計算
| 平均平方 | 公式 | 計算 | 結果 |
|---|---|---|---|
| VR(回帰) | SR ÷ φR | 48.93 ÷ 2 | 24.47 |
| Ve(残差) | Se ÷ φe | 0.27 ÷ 2 | 0.135 |
🔢 Step 3:F値を計算
🎉 完成!分散分析表
| 要因 | 平方和 S | 自由度 φ | 平均平方 V | F値 F₀ |
|---|---|---|---|---|
| 回帰 R | 48.93 | 2 | 24.47 | 181.3 |
| 残差 e | 0.27 | 2 | 0.135 | − |
| 計 T | 49.20 | 4 | − | − |
F₀ = 181.3 は非常に大きな値です。これは「回帰によるバラつき」が「残差(誤差)によるバラつき」の181倍以上あることを意味します。
つまり、この重回帰モデルは非常によく当てはまっていると言えそうです。
ただし、「F₀が大きい」だけでは統計的に有意とは言えません。次の記事で、F表と比較して正式に判定する方法を学びます。
【計算例あり】重回帰モデルの有意性検定|F₀とF表を比較して判定 →
📋 まとめ
この記事では、重回帰分析の分散分析表の作り方を解説しました。
- 分散分析表は「バラつきを要因ごとに整理した表」
- 自由度:φR = k、φe = n−k−1、φT = n−1
- 平均平方:V = S ÷ φ(1自由度あたりのバラつき)
- F値:F₀ = VR ÷ Ve(シグナル÷ノイズ)
- F値が大きいほど、回帰モデルは有効
【計算の流れ】
平方和 S → 自由度 φ → 平均平方 V → F値 F₀
分散分析表が完成したら、次はF表と比較して「統計的に有意かどうか」を正式に判定します。
📚 次に読むべき記事
F検定で「このモデルは統計的に有意か?」を判定する
各偏回帰係数が統計的に有意かを個別に検定する
偏回帰係数の信頼区間を計算する
【計算例あり】重回帰の平方和の分解|SR, Se, ST の意味と求め方 →
分散分析表の作り方完全ガイド|S→V→Fの流れを総復習 →
決定係数(R²)の正体|「あてはまりの良さ」を視覚的に理解する →
【図解】偏回帰係数とは?|「他を固定したときの影響度」を完全理解 →