😓「回帰分析で分散分析表が出てきたけど、何を計算しているの?」
😓「SR、Se、STって何の略?どうやって求めるの?」
😓「F検定で"有意"って判定されたけど、何が言えるの?」
こんな疑問、抱えていませんか?
回帰直線を引いただけでは、「その直線が本当に意味があるのか」がわかりません。分散分析表を使えば、回帰式の有意性を客観的に判定できます。
💡 結論ファースト
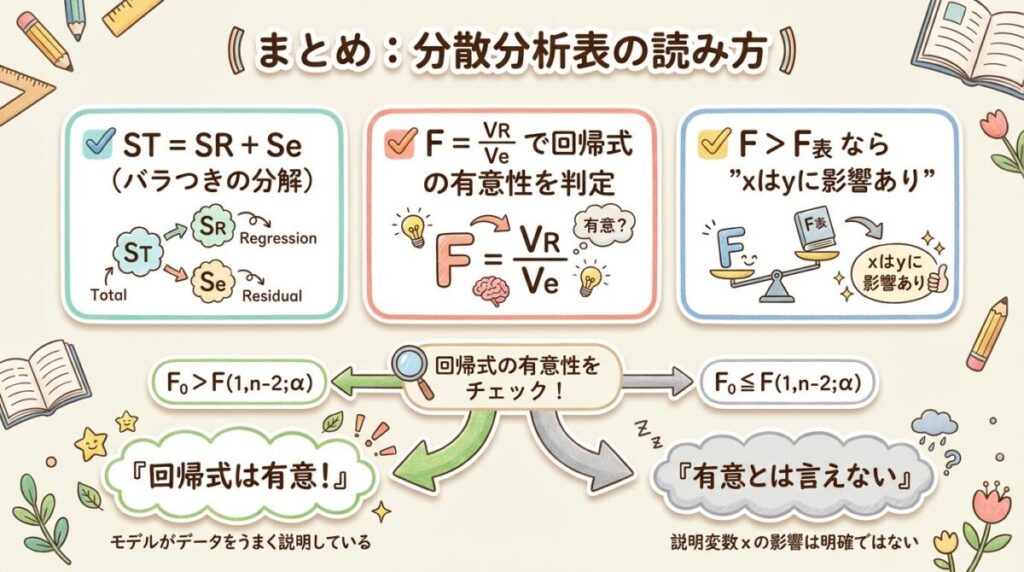
回帰分析の分散分析表は、yのバラつき(ST)を「回帰で説明できる部分(SR)」と「説明できない残差(Se)」に分解します。F検定で「SR/Se」の比が大きければ、回帰式は有意(xはyに影響する)と判定できます。
📚 この記事でわかること
- 3つの平方和(ST, SR, Se)の意味と計算方法
- 分散分析表の構造と作り方
- F検定で回帰式の有意性を判定する方法
- 計算例で手を動かして完全理解
📌 前提知識:単回帰分析の基礎を理解している方向けです。まだの方は以下もどうぞ。
→ 回帰分析とは?「未来を予測する」仕組み
→ 最小二乗法とは?回帰直線を引く仕組み
目次
📊 3つの平方和を理解する
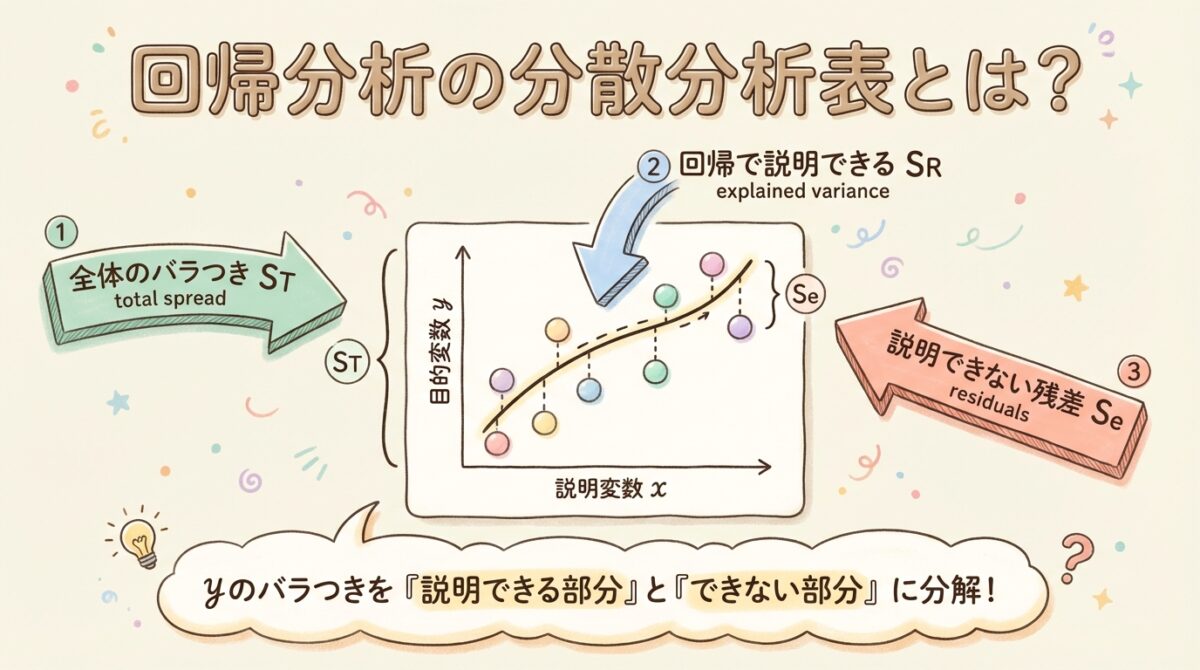
回帰分析の分散分析では、yのバラつき(変動)を3つに分解します。これが分散分析表の基本です。
🎯 バラつき分解の基本式
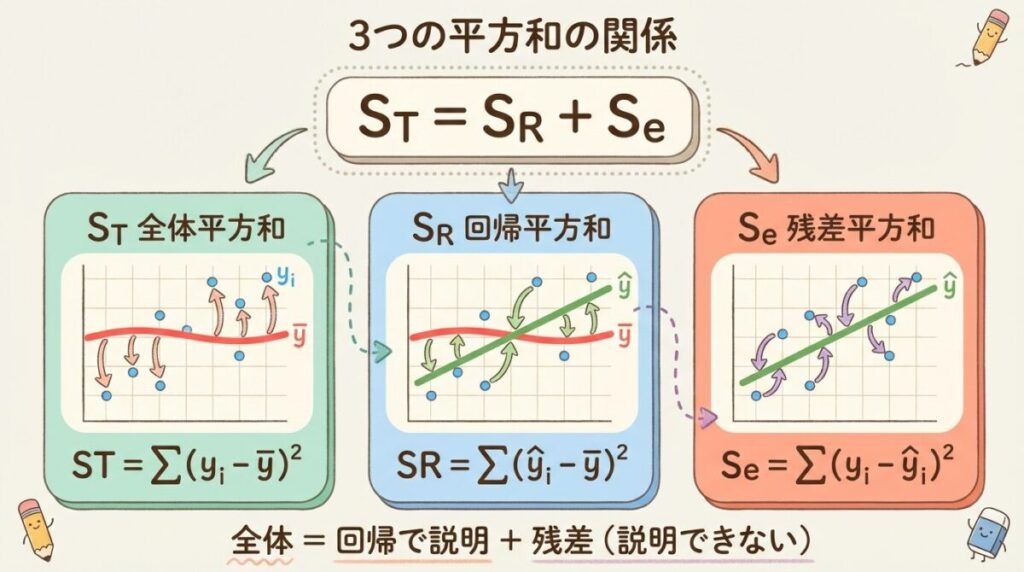
ST = SR + Se
全体のバラつき = 回帰で説明できる部分 + 説明できない残差
📐 各平方和の定義
ST:全体平方和
Total Sum of Squares
ST = Σ(yi − ȳ)²
意味:各データが平均ȳからどれだけ離れているか(yの全バラつき)
SR:回帰平方和
Regression Sum of Squares
SR = Σ(ŷi − ȳ)²
意味:回帰直線上の予測値が平均からどれだけ離れているか(回帰で説明できる部分)
Se:残差平方和
Error Sum of Squares
Se = Σ(yi − ŷi)²
意味:実測値と予測値のズレ(回帰で説明できない残差)
☕ イメージで理解:テストの点数
生徒の数学の点数(y)を、勉強時間(x)で予測する場面を想像してください。
ST:生徒ごとの点数のバラつき(全体の散らばり)
SR:「勉強時間」で説明できる点数の差
Se:勉強時間では説明できない個人差(才能、体調など)
SR が大きいほど「勉強時間が点数に影響している」と言えます。
📏 決定係数R²との関係
実は、決定係数R²は平方和を使って表せます。
R² = SR/ST = 1 − Se/ST
R² = 「全体のバラつきのうち、回帰で説明できる割合」
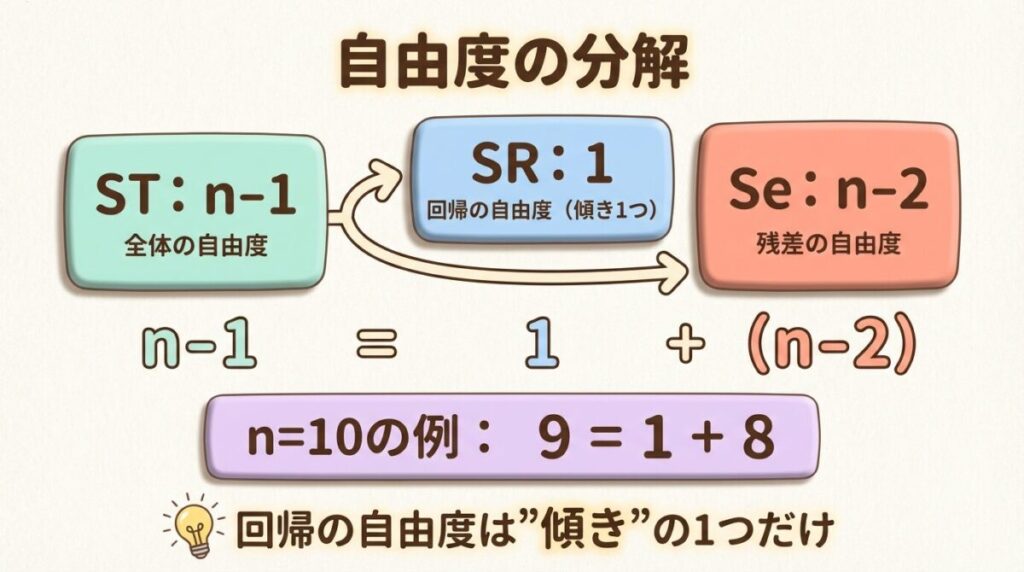
📐 自由度の分解
平方和だけでなく、自由度も分解されます。これが分散分析表の重要なポイントです。
🔢 自由度の内訳
φT = φR + φe
(n − 1) = 1 + (n − 2)
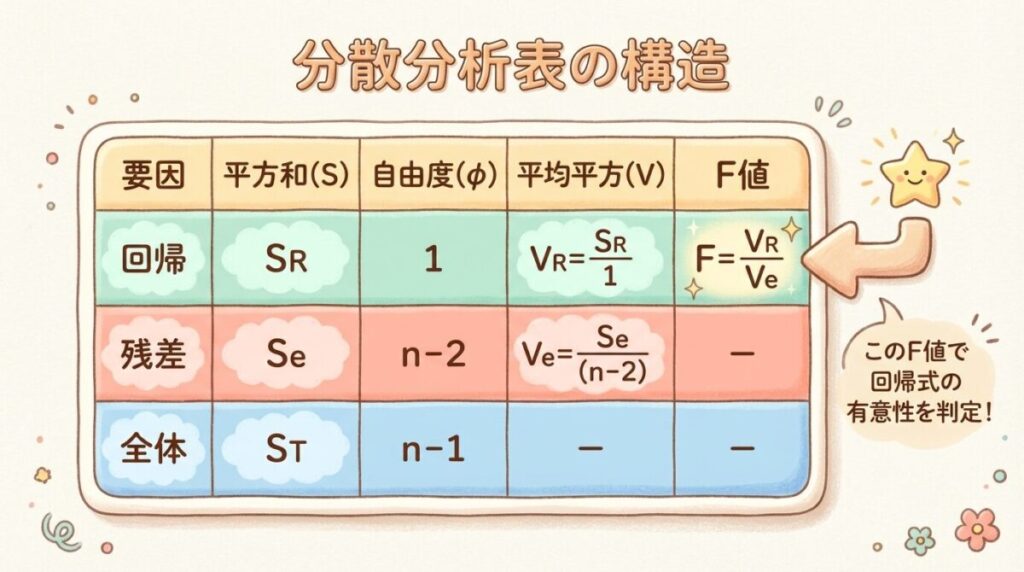
📋 分散分析表の構造
分散分析表は、以下の5列で構成されます。
📊 分散分析表のテンプレート
| 要因 | 平方和 S | 自由度 φ | 平均平方 V | F値 |
|---|---|---|---|---|
| 回帰 R | SR | 1 | VR = SR/1 | F₀ = VR/Ve |
| 残差 e | Se | n − 2 | Ve = Se/(n−2) | − |
| 全体 T | ST | n − 1 | − | − |
各列の意味:
- 平方和 S:バラつきの大きさ(二乗和)
- 自由度 φ:自由に動ける値の数
- 平均平方 V:平方和 ÷ 自由度(分散の推定値)
- F値:VR/Ve(回帰の効果 ÷ 誤差の比)
🎯 F検定の判定方法
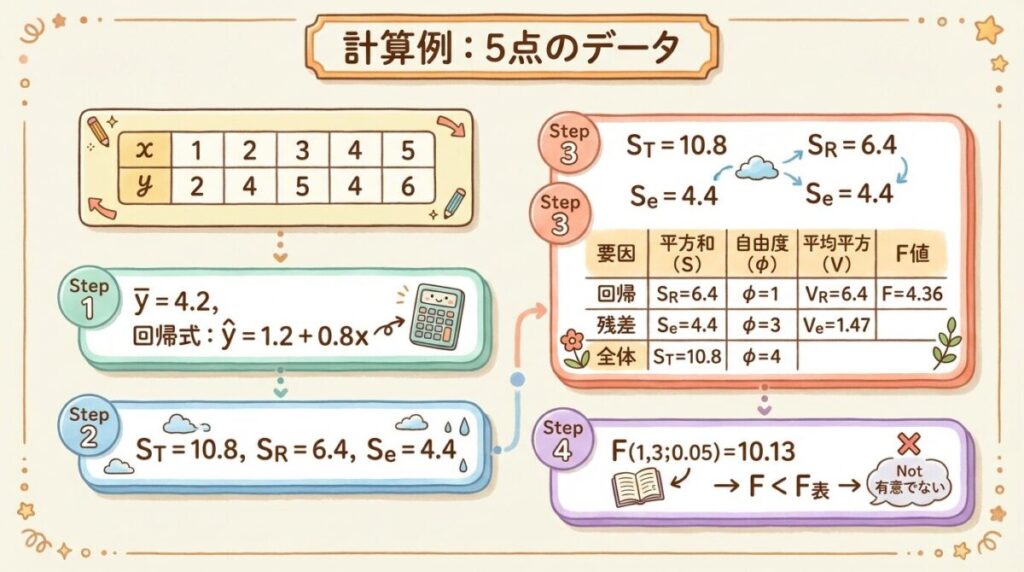
🧮 計算例:5点のデータで分散分析表を作成
以下のデータを使って、分散分析表を作成し、回帰式の有意性を検定してみましょう。
データ(n = 5)
| i | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| x | 1 | 2 | 3 | 4 | 5 |
| y | 2 | 4 | 5 | 4 | 6 |
Step 1:基本統計量の計算
平均:x̄ = (1+2+3+4+5)/5 = 3 , ȳ = (2+4+5+4+6)/5 = 4.2
偏差の積和:Σ(x−x̄)(y−ȳ) = (−2)(−2.2) + (−1)(−0.2) + (0)(0.8) + (1)(−0.2) + (2)(1.8) = 4.4 + 0.2 + 0 − 0.2 + 3.6 = 8
xの偏差平方和:Σ(x−x̄)² = 4 + 1 + 0 + 1 + 4 = 10
Step 2:回帰係数の計算
傾き b = Σ(x−x̄)(y−ȳ) / Σ(x−x̄)² = 8 / 10 = 0.8
切片 a = ȳ − b × x̄ = 4.2 − 0.8 × 3 = 1.8
回帰式:ŷ = 1.8 + 0.8x
Step 3:予測値ŷの計算
| i | x | y | ŷ = 1.8+0.8x | y − ȳ | ŷ − ȳ | y − ŷ |
|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 2.6 | −2.2 | −1.6 | −0.6 |
| 2 | 2 | 4 | 3.4 | −0.2 | −0.8 | +0.6 |
| 3 | 3 | 5 | 4.2 | +0.8 | 0 | +0.8 |
| 4 | 4 | 4 | 5.0 | −0.2 | +0.8 | −1.0 |
| 5 | 5 | 6 | 5.8 | +1.8 | +1.6 | +0.2 |
Step 4:3つの平方和を計算
ST = Σ(y−ȳ)² = (−2.2)² + (−0.2)² + (0.8)² + (−0.2)² + (1.8)² = 4.84 + 0.04 + 0.64 + 0.04 + 3.24 = 10.8
SR = Σ(ŷ−ȳ)² = (−1.6)² + (−0.8)² + (0)² + (0.8)² + (1.6)² = 2.56 + 0.64 + 0 + 0.64 + 2.56 = 6.4
Se = Σ(y−ŷ)² = (−0.6)² + (0.6)² + (0.8)² + (−1.0)² + (0.2)² = 0.36 + 0.36 + 0.64 + 1.0 + 0.04 = 2.4
検算:ST = SR + Se → 10.8 ≠ 6.4 + 2.4 = 8.8 ... ※丸め誤差あり
💡 簡便公式を使う方法
SR = b × Σ(x−x̄)(y−ȳ) = 0.8 × 8 = 6.4
Se = ST − SR = 10.8 − 6.4 = 4.4(こちらが正確)
Step 5:分散分析表の完成
| 要因 | 平方和 S | 自由度 φ | 平均平方 V | F₀ |
|---|---|---|---|---|
| 回帰 R | 6.4 | 1 | 6.4 | 4.36 |
| 残差 e | 4.4 | 3 | 1.47 | − |
| 全体 T | 10.8 | 4 | − | − |
F₀の計算:F₀ = VR / Ve = 6.4 / 1.47 = 4.36
⚖️ F検定による判定
📊 F分布表との比較
有意水準α = 0.05で検定します。
F分布表より:F(1, 3; 0.05) = 10.13
計算したF値:F₀ = 4.36
判定結果
F₀ = 4.36 < F(1, 3; 0.05) = 10.13
→ 帰無仮説を棄却できない(有意水準5%で有意とは言えない)
📊 結果の解釈
この例では、「xがyに影響する」とは言えないという結果になりました。
ただし、これは「影響がない」ことを証明したわけではありません。サンプルサイズがn=5と小さいため、効果を検出するパワーが不足している可能性があります。
参考:R² = SR/ST = 6.4/10.8 = 0.59(回帰で59%を説明)
📌 まとめ
- 分散分析表はyのバラつきを分解する:ST = SR + Se
- ST:全体のバラつき、SR:回帰で説明、Se:残差
- 自由度:全体(n−1) = 回帰(1) + 残差(n−2)
- F₀ = VR/Ve で回帰式の有意性を検定
- F₀ > F(1, n−2; α) なら「xはyに影響する」と言える
📐 公式まとめ
ST = Σ(yi − ȳ)²
SR = Σ(ŷi − ȳ)² = b × Σ(xi − x̄)(yi − ȳ)
Se = ST − SR
F₀ = (SR/1) / (Se/(n−2))
💡 試験対策のポイント
QC検定や統計検定では、分散分析表の空欄を埋める問題が頻出です。「SR = b × Sxy」の簡便公式を使えば計算が速くなります。また、自由度の分解(n−1 = 1 + n−2)を覚えておくと確実に得点できます。
最後までお読みいただきありがとうございました!
ご質問・ご感想は @shirasusolo までお気軽にどうぞ。