- 新製品を3台テストしたけど、1台も壊れなかった。MTBFはどう報告すればいい?
- 「故障ゼロ」なら「MTBF=無限大」と言っていいの?
- 指数分布とか二項分布とか、なぜその式を使うのかピンとこない…
- QC検定1級の信頼性工学の問題が全然解けない…
- 確率分布の基本(離散型と連続型の違い)
- 二項分布と指数分布の「なぜ使うのか」
- 故障ゼロからMTBFの下限を求める公式の導出
- 具体的な計算例で完全マスター
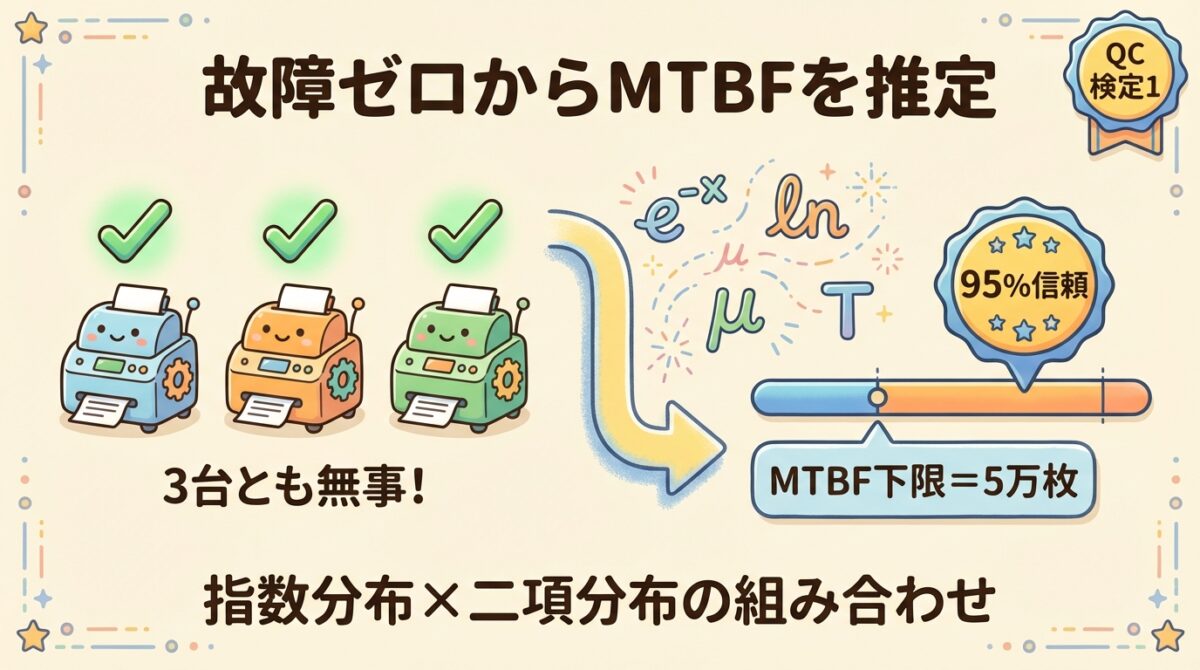
「3台テストして、全部無事だった!」
これは嬉しい結果ですよね。でも、上司に「MTBFはいくつ?」と聞かれたら、どう答えますか?
「故障ゼロだから、MTBFは無限大です!」…とは言えませんよね。たまたま運が良かっただけかもしれないからです。
この記事では、故障が1回も起きなかったデータから、「少なくともMTBFはこれ以上ある」と言える下限値を統計的に求める方法を解説します。
故障ゼロでも「MTBFは少なくとも○○以上」と言える。その公式は:
n=台数、T=試験時間、α=有意水準(5%なら0.05)
では、なぜこの式になるのか?を一緒に理解していきましょう。
目次
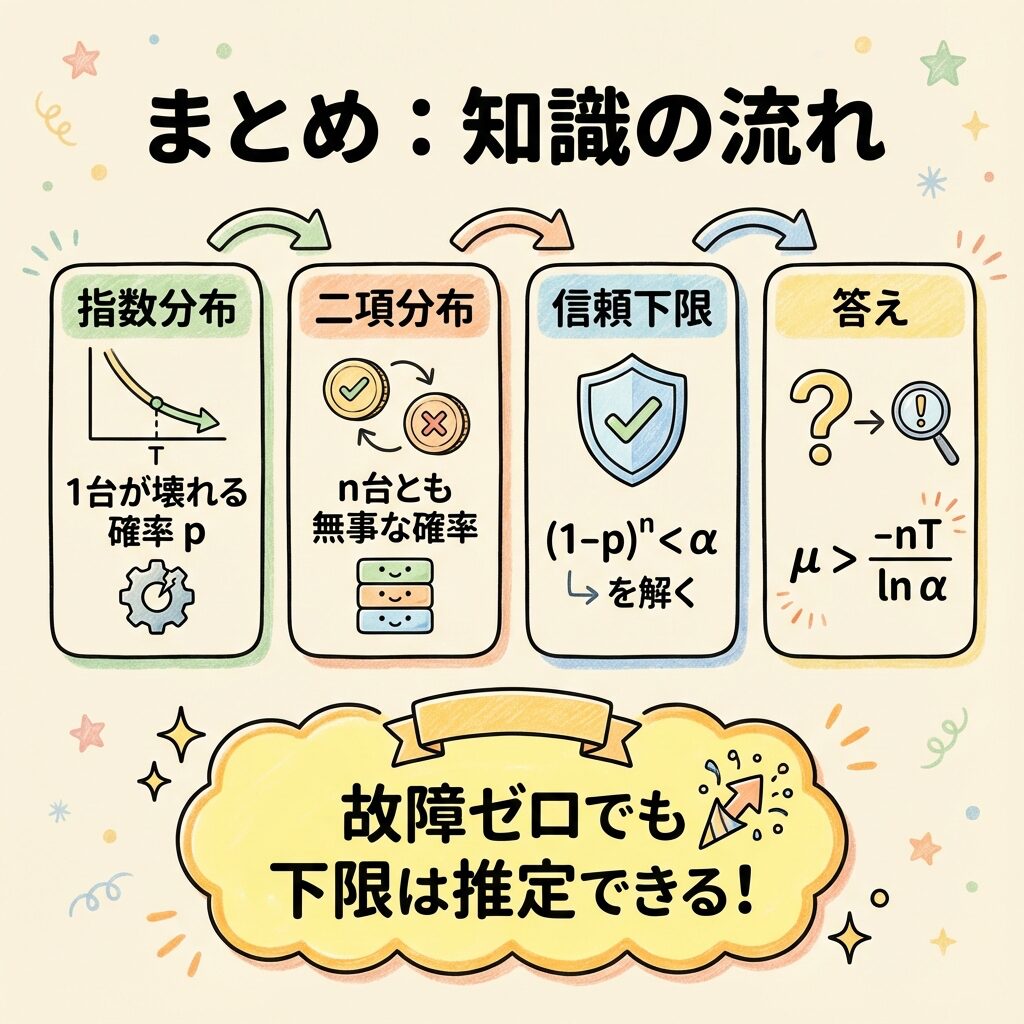
🗺️ 全体像:この記事で学ぶ「知識のつながり」
まず、これから学ぶ内容の「地図」を頭に入れておきましょう。
この問題を解くには、4つの知識を順番に積み上げる必要があります。
| STEP | 学ぶこと | この問題での役割 |
|---|---|---|
| 1 | 確率分布の基本 | 離散型・連続型の違いを理解 |
| 2 | 二項分布 | 「n台中0台故障」の確率を計算 |
| 3 | 指数分布 | 「1台が故障する確率p」を計算 |
| 4 | 信頼下限の導出 | 2つを組み合わせて公式を導く |
この「知識の積み木」を、下から順番に積み上げていきます。焦らず、一つずつ理解していきましょう。

📊 STEP 1:確率分布って何?|「バラつき」を整理する道具
🎲 確率分布とは「結果の出やすさを整理した表」
確率分布という言葉、難しく聞こえますよね。でも、本質はシンプルです。
「起こりうる結果」と「その確率」を一覧にしたもの
サイコロを例に考えてみましょう。サイコロを1回振ると、1〜6のどれかの目が出ますよね。
| 出る目 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 確率 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
↑ これが「確率分布」です!結果とその確率を整理しただけ。難しくないですよね。
📈 確率分布の2つのタイプ:離散型と連続型
確率分布は大きく2種類に分かれます。今回の問題では、両方を使います。
| タイプ | 特徴 | 例 |
|---|---|---|
| 離散型 | 取りうる値が飛び飛び(整数など) | サイコロの目(1,2,3...) 故障した台数(0,1,2...) |
| 連続型 | 取りうる値が連続(小数も含む) | 故障までの時間(3.5時間、100.7時間...) 身長(165.3cm、172.8cm...) |
・二項分布(離散型)→ n台のうち「何台壊れたか」
・指数分布(連続型)→ 1台が「いつ壊れるか」
🎯 STEP 2:二項分布を理解する|「成功 or 失敗」の繰り返し
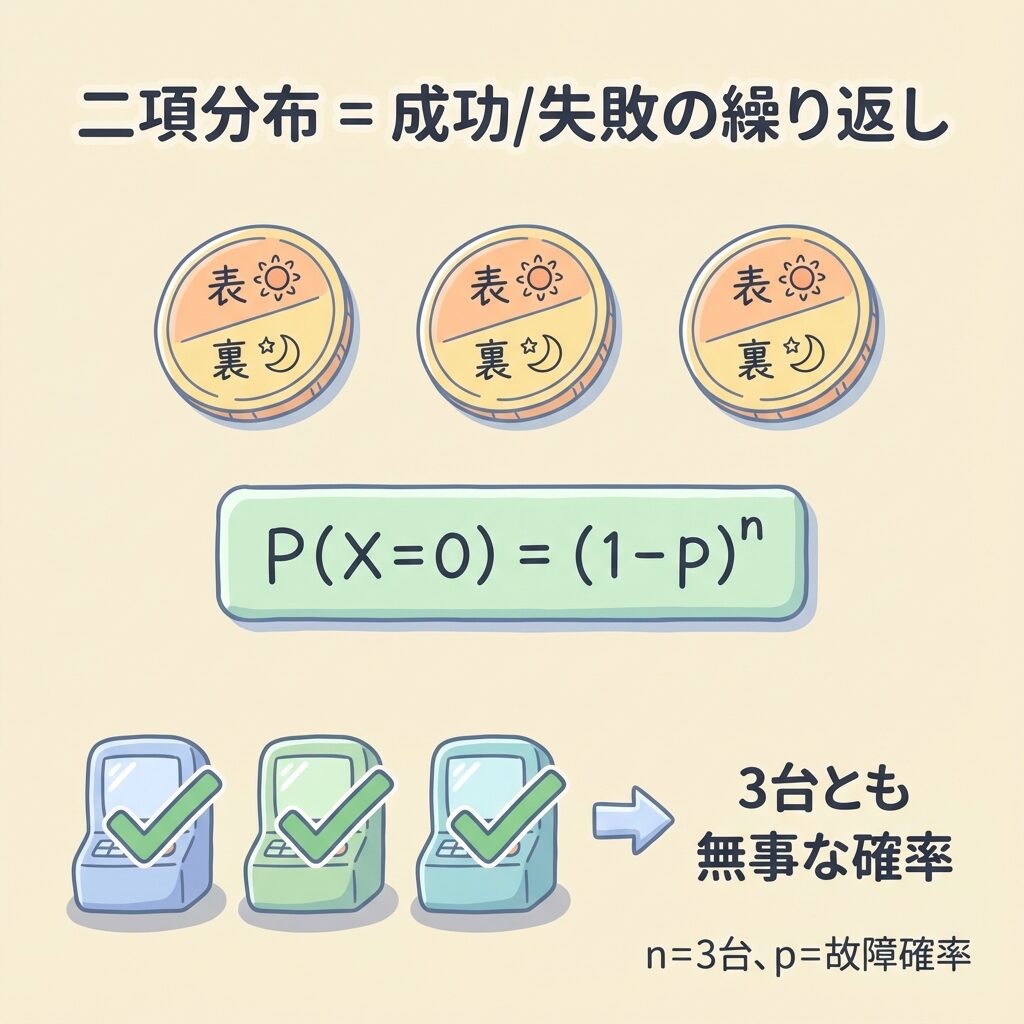
🪙 二項分布とは「コイン投げ」のような状況
二項分布は、次のような状況で使う分布です。
- 結果が「成功」か「失敗」の2択である
- 成功確率 p が毎回同じである
- 各試行が独立している(前の結果が次に影響しない)
- 試行回数 n が決まっている
コイン投げがまさにこの条件を満たしますよね。表が出るか、裏が出るか。毎回確率は50%。前の結果は次に影響しない。
🪙 具体例:コインを3回投げたとき
コインを3回投げて、表が出る回数の確率分布を考えてみましょう。
| 表が出た回数 | パターン | 確率 |
|---|---|---|
| 0回 | 裏裏裏 | 0.5³ = 0.125 |
| 1回 | 表裏裏, 裏表裏, 裏裏表 | 3 × 0.5³ = 0.375 |
| 2回 | 表表裏, 表裏表, 裏表表 | 3 × 0.5³ = 0.375 |
| 3回 | 表表表 | 0.5³ = 0.125 |
注目してほしいのは「0回」の確率 = 0.125です。これは「3回とも裏」が出る確率。
計算式で書くと:(1 − 0.5)³ = 0.5³ = 0.125
🏭 信頼性試験に当てはめると?
コイン投げを、信頼性試験に置き換えてみましょう。
| コイン投げ | 信頼性試験 |
|---|---|
| 投げる回数 n | 試験する製品の台数 n |
| 表が出る確率 p | 1台が故障する確率 p |
| 表が0回(全部裏) | 故障0台(全部無事) |
pは1台が故障する確率、nは試験台数
この式が、二項分布から得られる「n台すべてが無事な確率」です。次は、pの値をどう求めるかを見ていきましょう。
⏱️ STEP 3:指数分布を理解する|「いつ壊れるか」の分布
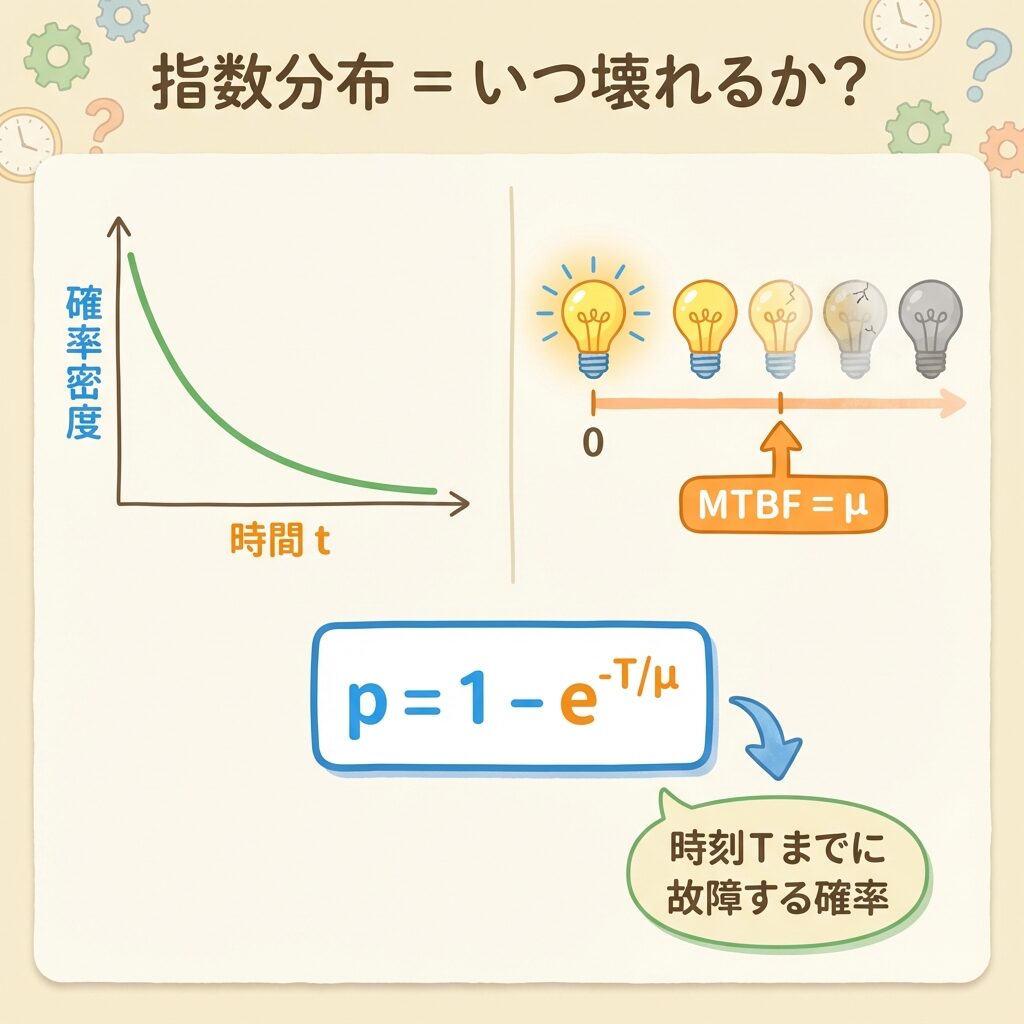
💡 指数分布とは「待ち時間」の分布
指数分布は、「次に何かが起きるまでの時間」をモデル化する分布です。
身近な例で言うと:
- 電球が切れるまでの時間
- 機械が故障するまでの時間
- コンビニに次のお客さんが来るまでの時間
共通点は、「いつ起きるかランダムだけど、平均的な間隔は分かっている」という状況です。
🔢 指数分布で覚えるべき式(3つだけ!)
指数分布で覚えるべき式は3つだけです。
| 名前 | 式 | 意味 |
|---|---|---|
| 故障率とMTBF | λ = 1/μ | λ:故障率、μ:MTBF(平均故障間隔) |
| 故障する確率 | p = 1 − e−T/μ | 時刻Tまでに故障する確率 |
| 生存する確率 | R(T) = e−T/μ | 時刻Tまで故障しない確率 |
今回使うのは、2番目の「故障する確率」の式です。
T:試験時間、μ:MTBF(平均故障間隔)
🤔 なぜこの式になるのか?|イメージで理解
「なぜ e のマイナス乗なの?」と疑問に思いますよね。直感的に説明します。
時刻0:生存率 100%(みんな元気)
時刻1:生存率 90%(10%が脱落)
時刻2:生存率 81%(残りの10%が脱落)
時刻3:生存率 72.9%(残りの10%が脱落)
「残りのうち一定割合が減っていく」
→ これを数式で表すと e−λt になる!
e−T/μ は、「毎瞬間、一定の確率で壊れるリスクがあるとき、時刻Tまで生き残る確率」を表しています。
📝 具体例で計算してみよう
電球のMTBFが1000時間だとします。500時間後までに切れる確率は?
| ステップ | 計算 |
|---|---|
| 条件 | μ = 1000時間、T = 500時間 |
| 式に代入 | p = 1 − e−500/1000 = 1 − e−0.5 |
| 計算 | p = 1 − 0.607 = 0.393 |
| 答え | 500時間後までに切れる確率は約39% |
MTBFが1000時間の電球でも、500時間で約4割は切れるということです。意外と早く壊れるんですね。
第15回:指数分布 - 連続的な待ち時間分布 →
🔗 STEP 4:2つの分布を組み合わせる|信頼下限を導出する
🧩 指数分布と二項分布の役割分担
ここまで学んだ2つの分布を、今回の問題にどう使うか整理しましょう。
| 分布 | 役割 | 式 |
|---|---|---|
| 指数分布 | 1台が故障する確率 p を計算 | p = 1 − e−T/μ |
| 二項分布 | n台すべて無事な確率を計算 | P(X=0) = (1−p)n |
ここで重要なのは、1−p = e−T/μ(故障しない確率)です。これを二項分布の式に代入すると:
🎯 信頼下限の考え方|ここが一番難しい!
「信頼下限」とは、「95%の確信を持って、MTBFは少なくともこれ以上ある」と言える値です。
考え方のポイントを、宝くじのたとえで説明します。
状況:宝くじを3枚買って、3枚ともハズレだった。
考え方:
・当選確率が50%なら → 3枚ともハズレは珍しい(確率12.5%)
・当選確率が10%なら → 3枚ともハズレは普通(確率72.9%)
・当選確率が1%なら → 3枚ともハズレは当然(確率97.0%)
「3枚ともハズレ」という結果から、当選確率の上限を推定できる!
信頼性試験でも同じ考え方をします。
状況:3台テストして、3台とも故障なしだった。
考え方:
・もしMTBFが小さいなら → 故障確率pが高い → 3台無事は珍しい
・もしMTBFが大きいなら → 故障確率pが低い → 3台無事は普通
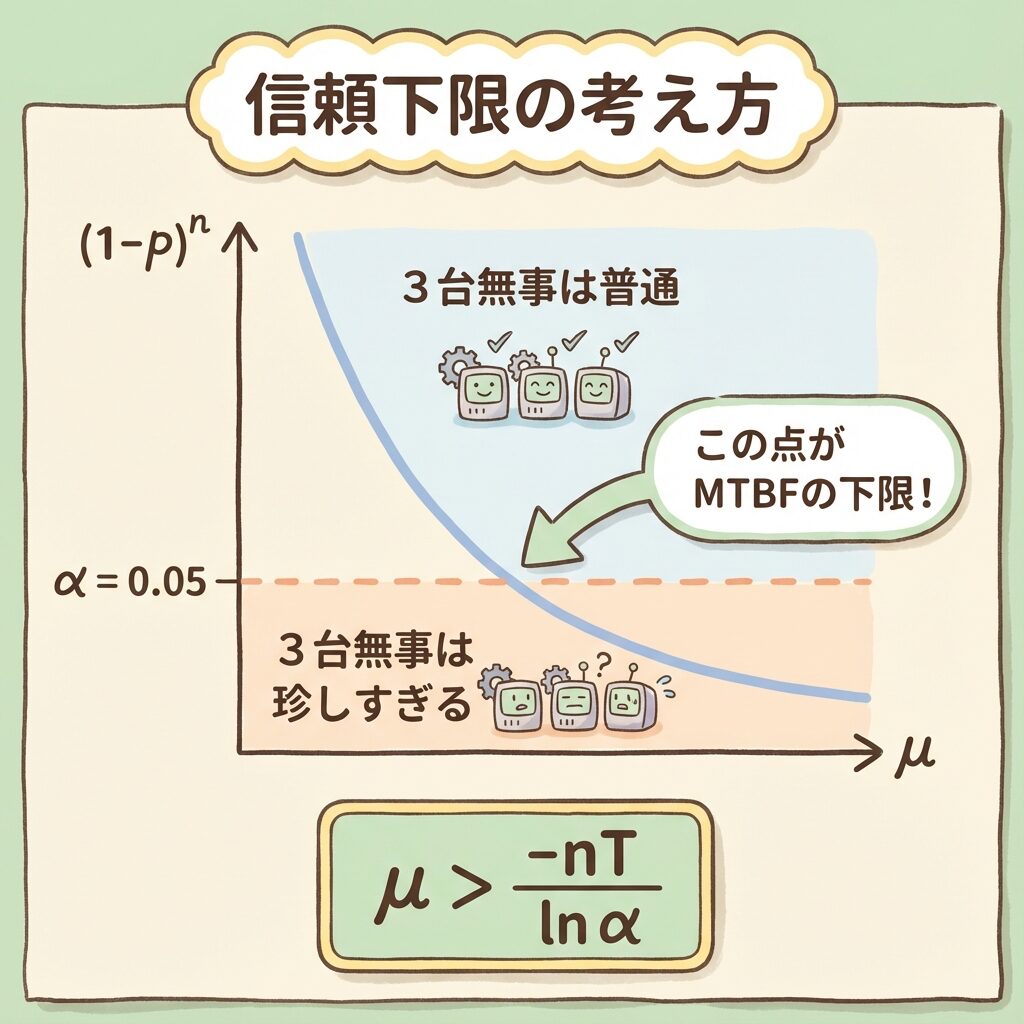
「3台とも無事なのが、確率α(5%)以下になる」ギリギリのMTBFが信頼下限!
数式で表すと:
「n台すべて無事な確率がα以下になる」ところがMTBFの下限
🧮 式を解く(対数を使う)
e の指数が入った式を解くには、自然対数(ln)を使います。
| ステップ | 計算 |
|---|---|
| 1 | (e−T/μ)n < α → e−nT/μ < α |
| 2 | 両辺の自然対数をとる:−nT/μ < ln α |
| 3 | ln α は負の数なので、割ると不等号が逆転 |
| 結果 | μ > −nT / ln α |
α = 0.05 のとき、ln 0.05 ≈ −2.996
負の数で割ると、不等号の向きが逆転します。これを忘れると答えが間違います!
🔢 具体的な数値で計算してみよう
では、実際の問題を解いてみましょう。
・試験台数 n = 3台
・試験時間 T = 50,000枚
・結果:故障0台
・信頼率 95%(α = 0.05)
・ln 0.05 = −2.996
| ステップ | 計算 |
|---|---|
| 公式 | μ > −nT / ln α |
| 数値代入 | μ > −(3 × 50,000) / (−2.996) |
| 計算 | μ > 150,000 / 2.996 = 50,067枚 |
| 答え | MTBFの信頼下限 ≈ 5万枚 |
「95%の確信を持って、MTBFは少なくとも5万枚以上ある」と言える!
📝 まとめ|この記事で学んだこと
この記事では、故障ゼロのテスト結果からMTBFの信頼下限を推定する方法を学びました。
STEP 1:確率分布 → 離散型と連続型の2種類がある
STEP 2:二項分布 → n台すべて無事な確率 = (1−p)n
STEP 3:指数分布 → 1台が故障する確率 p = 1 − e−T/μ
STEP 4:信頼下限 → (1−p)n < α を解いて μ > −nT / ln α
n=台数、T=試験時間、α=有意水準(5%なら0.05)
故障ゼロのテスト結果を報告するとき、「MTBFは無限大」ではなく「少なくとも○○以上」と言えるようになります。
これは品質保証や信頼性試験のレポートで非常に重要な考え方です。QC検定1級でも頻出のテーマなので、しっかり押さえておきましょう。
📚 次に読むべき記事
二項分布の基本を詳しく学びたい方はこちら
指数分布の詳しい解説と他の応用例を学びたい方はこちら
確率分布の基礎をさらに深めたい方はこちら