- 「固有値」「固有ベクトル」…漢字を見るだけで頭が痛くなる
- 教科書を読んでも、結局何をやっているのかわからない
- 数式が出てきた瞬間に眠くなる
イラストを見るだけで、7つの用語のイメージがつかめるようになります。
数式は最小限。図解がすべてです。
目次
そもそも主成分分析って何?|「テストの総合点」で理解する
まず、主成分分析が「何をするものか」をイメージしましょう。
想像してください。あなたは先生で、生徒の成績を比較したいとします。

主成分分析 = たくさんの項目を「少数の総合点」にまとめる技術
国語・数学・英語・理科・社会の5教科があったとき、それぞれの点数をバラバラに見ても「この人、結局頭いいの?」がわかりにくいですよね。
そこで、5教科を「文系力」「理系力」という2つの総合点にまとめる。これが主成分分析のやっていることです。
では、この「まとめる」プロセスで出てくる7つの用語を、順番に見ていきましょう。
用語①:分散共分散行列|「相性チェック表」
まず最初に作るのが分散共分散行列です。
名前は怖いですが、やっていることはシンプル。「各項目同士の相性チェック表」を作っているだけです。
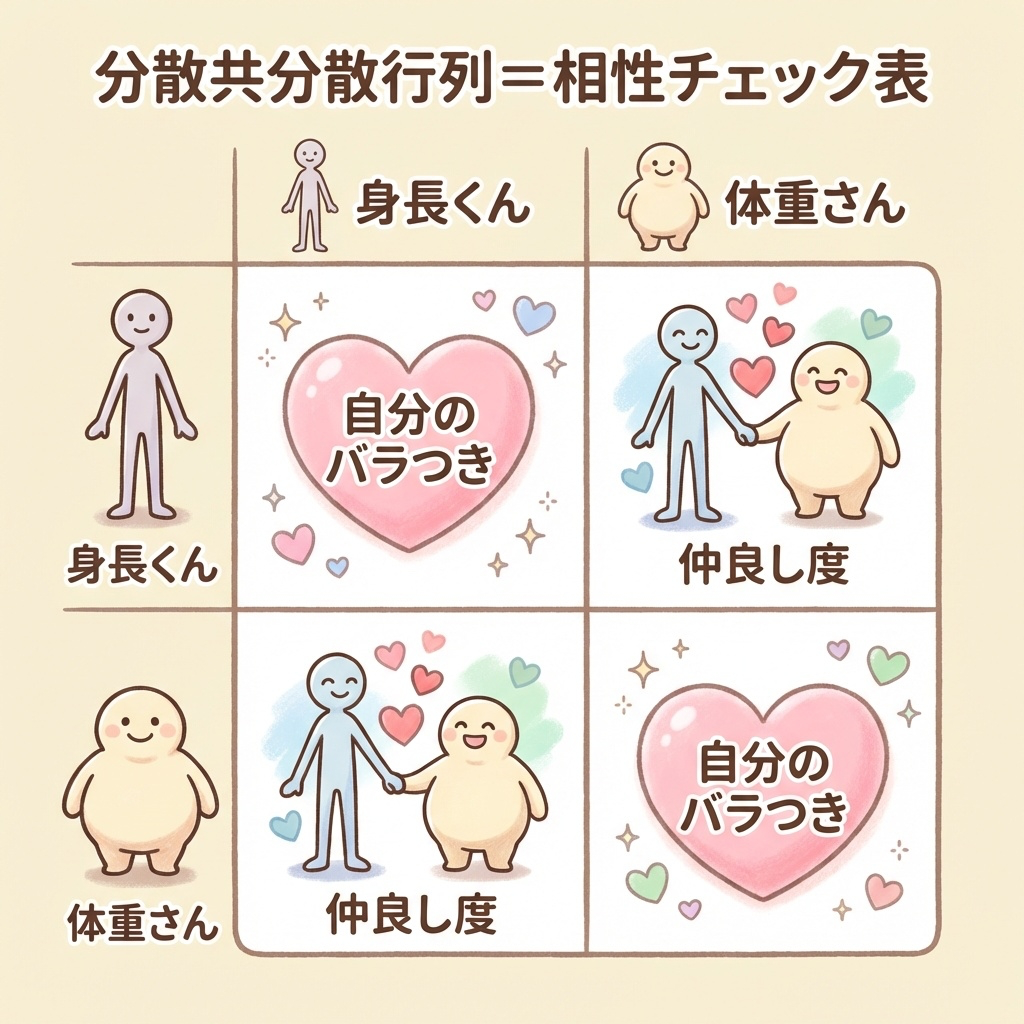
分散共分散行列 = 「誰と誰が仲良しか」を一覧にした表
身長と体重は仲良し(一緒に大きくなる傾向がある)。
身長と50m走はあまり関係ない。
こういう「変数同士の仲良し度」を全部調べて、表にまとめたものが分散共分散行列です。
共分散とは?|「気温が上がるとビールが売れる」を数値化する魔法の道具 →
用語②:固有ベクトル|「ベストな撮影アングル」
次は固有ベクトル。これも名前が怖いですね。
でも大丈夫。「集合写真のベストアングル」と考えればOKです。

固有ベクトル = データの「違い」が一番よく見えるカメラアングル
集合写真を撮るとき、アングルによって「個人の違い」がわかりやすかったり、わかりにくかったりしますよね。
データも同じです。ある角度から見ると、データの違いがハッキリ見える。その「ベストアングル」が固有ベクトルです。
第1固有ベクトル = 一番違いがわかるアングル
第2固有ベクトル = 二番目に違いがわかるアングル
…という具合です。
用語③:固有値|「違いの大きさ」
固有ベクトルが「アングル(方向)」なら、固有値は「そのアングルで見たときの違いの大きさ」です。
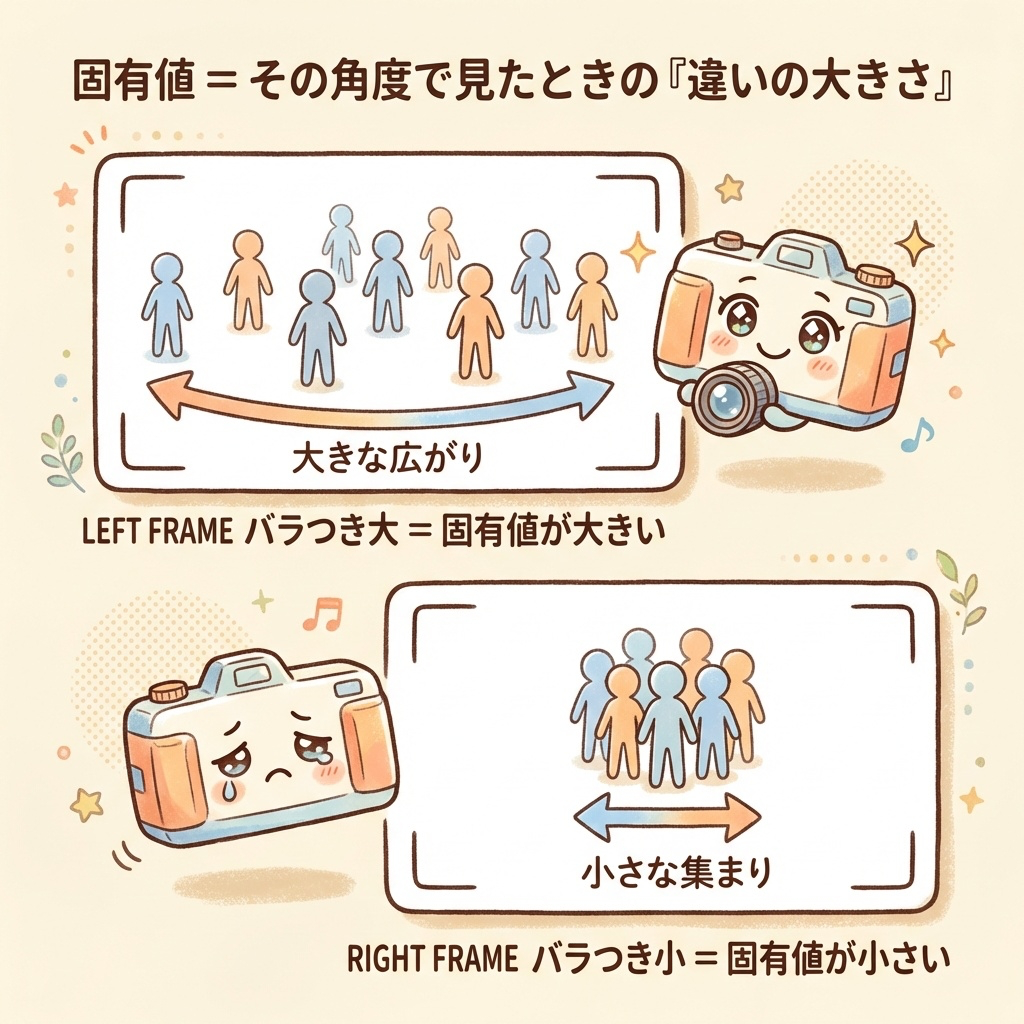
固有値 = そのアングルで見たとき、人がどれくらいバラけて見えるか
ベストアングル(第1固有ベクトル)から見ると、人がバラバラに広がって見える = 固有値が大きい
イマイチなアングルから見ると、人が重なって見える = 固有値が小さい
固有値 = その主成分の分散(バラつきの大きさ)
固有値が大きいほど、重要な情報がたくさん入っています。
用語④:寄与率|「パイの取り分」
寄与率は、「そのアングル(主成分)がどれくらい大事か」をパーセントで表したものです。
ホールケーキを切り分けるイメージで考えてみましょう。

寄与率 = 情報という「パイ」を、各主成分がどれだけ食べるか
第1主成分が60%、第2主成分が25%、第3主成分が15%…という具合に、全部足すと100%になります。
寄与率が大きい主成分ほど、「おいしい情報」をたくさん持っているということです。
用語⑤:累積寄与率|「積み上げ合計」
累積寄与率は、「第1主成分から順番に足していったら、合計何%になるか」です。
ブロックを積み上げるイメージです。

累積寄与率 = 「どこまで積めば十分か」の目安
一般的に、累積寄与率が70〜80%を超えたらOKとされています。
つまり、「情報の8割をカバーできるなら、残りの2割は捨てても大丈夫」という考え方です。
| 主成分 | 寄与率 | 累積寄与率 |
|---|---|---|
| 第1 | 60% | 60% |
| 第2 | 25% | 85% ✓ ここでOK! |
| 第3 | 15% | 100% |
用語⑥:因子負荷量|「磁石の引き寄せ力」
因子負荷量は、「その主成分がどの変数と仲良しか」を表す数字です。
磁石をイメージしてください。
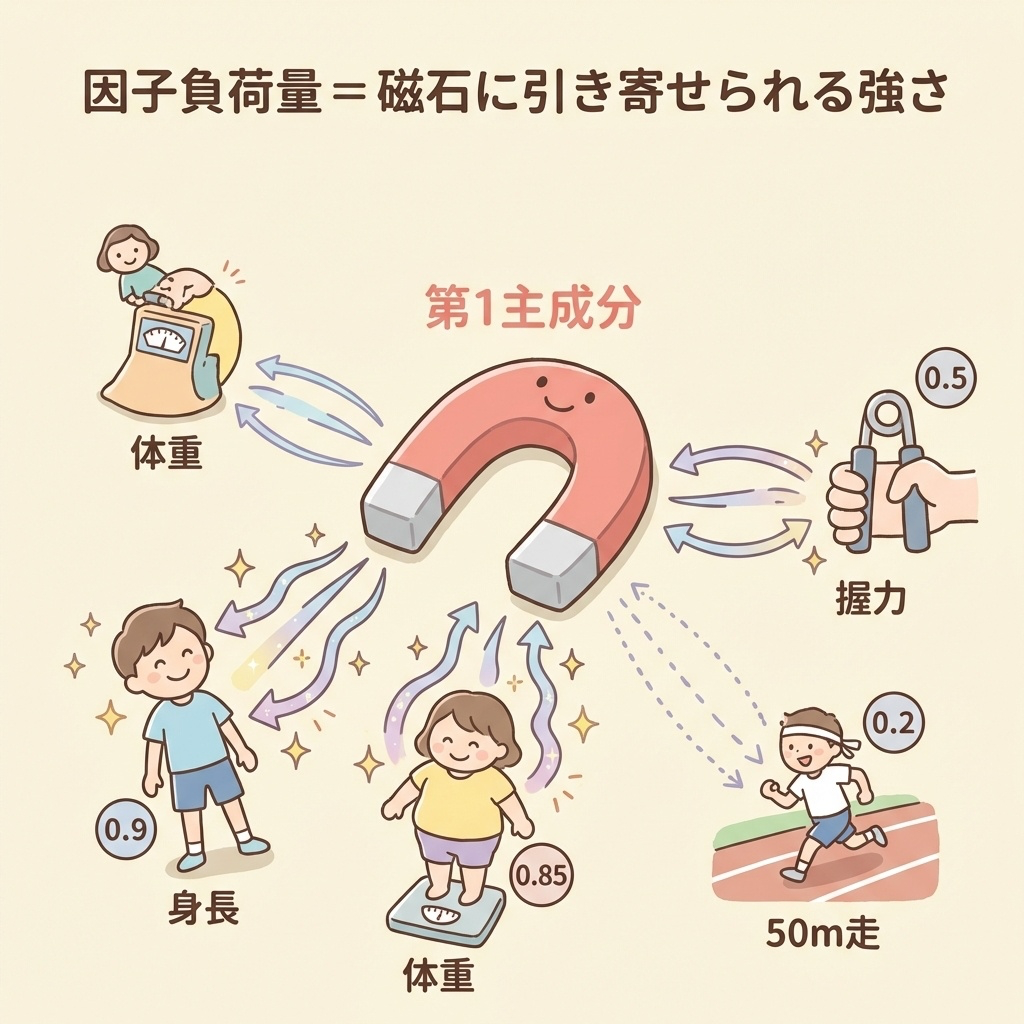
因子負荷量 = その主成分が各変数をどれくらい引き寄せているか
第1主成分という「磁石」があるとします。
身長と体重は磁石に強く引き寄せられている(因子負荷量が大きい)。
50m走はあまり引き寄せられていない(因子負荷量が小さい)。
この情報から、「第1主成分は『体格』を表している」と解釈できます。
因子負荷量 ≠ 固有ベクトル
因子負荷量 = 固有ベクトル × √固有値
「因子負荷量を求めよ」と言われたら、√固有値をかけるのを忘れずに!
用語⑦:主成分得点|「新しい成績表」
最後は主成分得点。これは、各人(各サンプル)の「新しい成績表」です。

主成分得点 = 5教科の成績を「文系力」「理系力」に変換した点数
今まで「国語80点、数学65点、英語75点…」とバラバラだった成績が、
「文系力: +1.5」「理系力: -0.3」
という2つの数字で表現できるようになります。
この「+1.5」「-0.3」が主成分得点です。0が平均で、プラスなら平均より上、マイナスなら平均より下を意味します。
全体の流れ|すごろくで理解する主成分分析
ここまでの7つの用語を、すごろくの流れで整理しましょう。
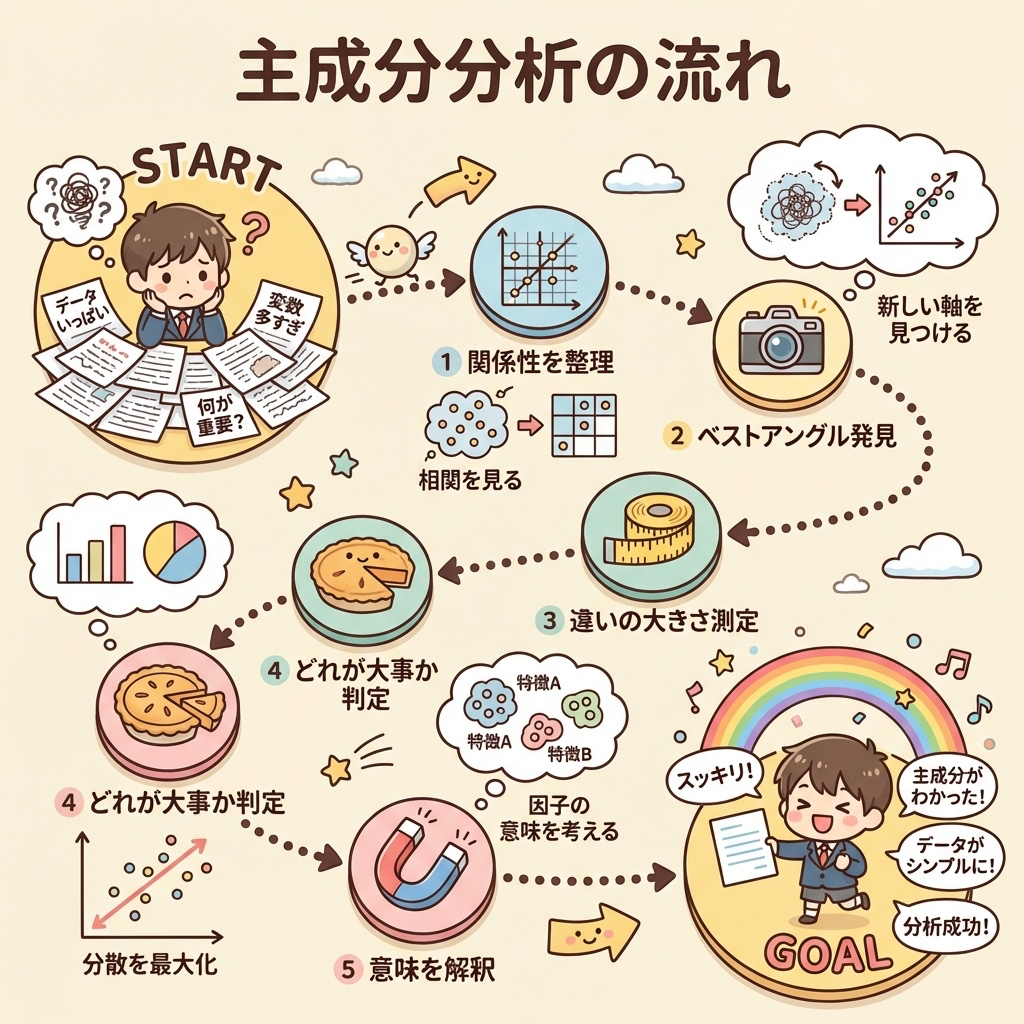
- スタート:データがいっぱいで混乱…
- 分散共分散行列:変数同士の「相性」をチェック
- 固有ベクトル:データの「ベストアングル」を発見
- 固有値:そのアングルの「違いの大きさ」を測定
- 寄与率:各アングルの「重要度」をパーセントで
- 累積寄与率:「ここまで使えばOK」のラインを確認
- 因子負荷量:主成分の「意味」を解釈
- 主成分得点:各人の「新しい成績」を計算
- ゴール!:データがスッキリ整理された!
なぜ主成分分析を使うの?|ビフォーアフター
「そもそも、なんでこんなことするの?」という疑問に答えます。
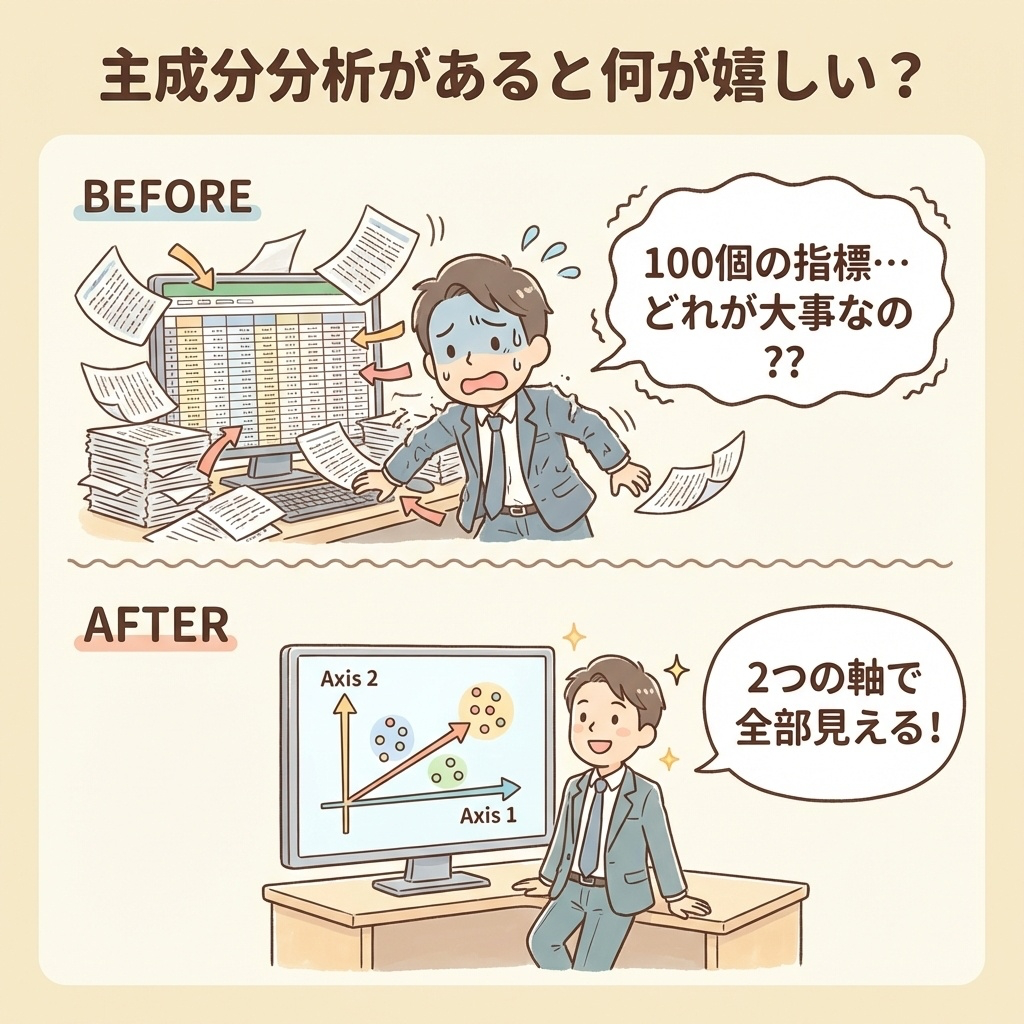
- 見える化:100個の項目も、2つの軸で散布図に描ける
- 比較が楽に:「総合点」で人やモノを比較できる
- ノイズ除去:重要な情報だけ残して、ムダを捨てられる
用語カード一覧|これだけ覚えればOK!
最後に、7つの用語を「カード」形式でまとめます。試験前の復習に使ってください。

| 用語 | イメージ | 一言で言うと |
|---|---|---|
| 分散共分散行列 | 📊 相性チェック表 | 変数同士の「仲良し度」を一覧にした表 |
| 固有ベクトル | 📷 ベストアングル | データの違いが一番よく見える方向 |
| 固有値 | 📏 違いの大きさ | そのアングルで見たときのバラつき量(= 分散) |
| 寄与率 | 🥧 パイの取り分 | 情報全体のうち、その主成分が占める割合(%) |
| 累積寄与率 | 🧱 積み上げ合計 | 第1〜第kまでの寄与率の合計(70〜80%が目安) |
| 因子負荷量 | 🧲 磁石の引き寄せ力 | 主成分と各変数の相関(= 固有ベクトル×√固有値) |
| 主成分得点 | 📝 新しい成績表 | 各サンプルの「新しい軸での点数」 |
まとめ|難しい用語も「イメージ」で攻略!
この記事では、主成分分析の7つの用語をイラストとたとえ話で解説してきました。
- 主成分分析 = たくさんの項目を「少数の総合点」にまとめる技術
- 固有ベクトル = ベストアングル(方向)
- 固有値 = 違いの大きさ(= 分散)
- 寄与率 = パイの取り分(%)
- 因子負荷量 = 磁石の引き寄せ力(主成分と変数の相関)
- 主成分得点 = 新しい成績表
数式は苦手でも、イメージさえつかめればQC検定の問題は解けます。この記事の図を何度も見返して、用語のイメージを定着させてください!
📚 次に読むべき記事
寄与率の計算練習をしたい方はこちら。計算問題で頻出のパターンを特訓できます。
因子負荷量をもっと詳しく学びたい方はこちら。計算方法と解釈のコツを解説。
主成分分析の「使い所」を知りたい方はこちら。実務での活用シーンを解説。
【完全版】統計学の勉強ロードマップ|初心者が「データ分析」を武器にするまでの全手順 →
