目次
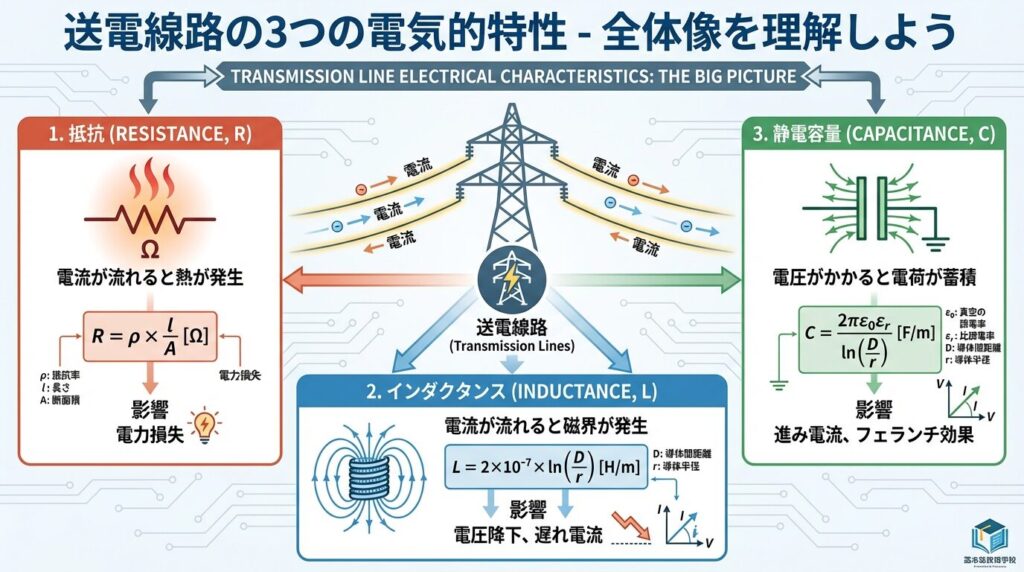
⚡ 送電線路の3つの電気的特性とは?
発電所から家庭まで電気を届ける送電線路。実は、単なる「電線」ではなく、3つの重要な電気的特性を持っています。
📊 送電線の3つの特性
- 抵抗(R):電流が流れると熱が発生 → 電力損失の原因
- インダクタンス(L):電流が流れると磁界が発生 → 電圧降下・遅れ電流
- 静電容量(C):電線間に電界が発生 → 充電電流・進み電流
💡 初心者向けの覚え方
送電線は「ただの導線」ではなく、抵抗・コイル・コンデンサの3つが合体したものと考えましょう!
この3つの特性が同時に存在し、送電線の性能を決めています。🎯
まずは全体像を確認しましょう! 👇
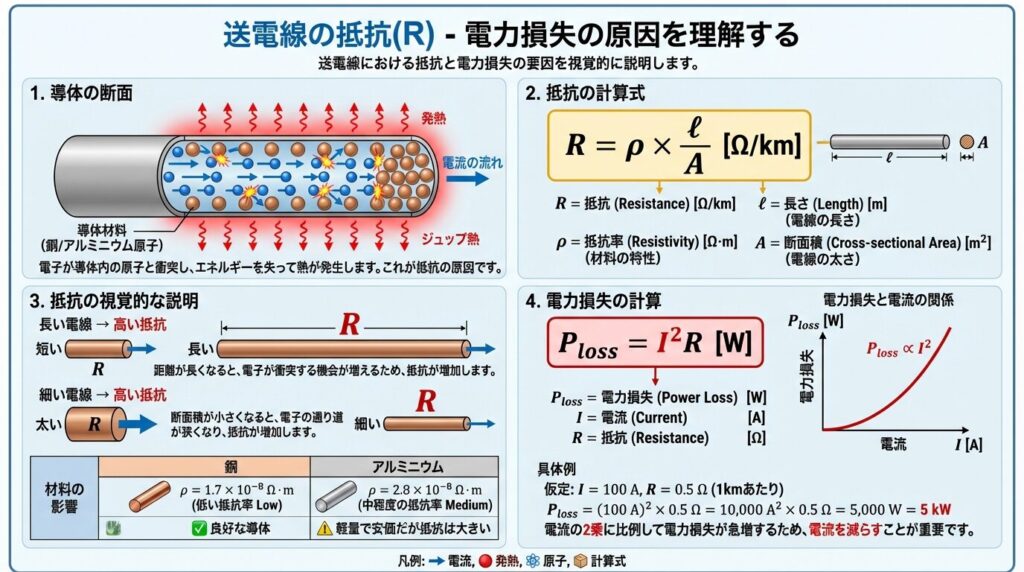
🔥 抵抗(R):電力損失の正体
送電線に電流が流れると、導体の抵抗によって熱が発生します。これが電力損失の主な原因です。
📐 抵抗の計算式
R = ρ × (l / A) [Ω/km]
ρ:抵抗率[Ω・m]、l:長さ[m]、A:断面積[m²]
🔍 抵抗に影響する3つの要素
① 導体の長さ(l)
長いほど抵抗が大きくなる 📏
→ 距離が2倍になると、抵抗も2倍!
② 導体の断面積(A)
太いほど抵抗が小さくなる 💪
→ 太い電線を使えば損失を減らせる!
③ 材質(抵抗率ρ)
銅(Cu):ρ = 1.7×10⁻⁸ Ω・m(低抵抗・高価)
アルミ(Al):ρ = 2.8×10⁻⁸ Ω・m(中抵抗・軽量・安価)
⚠️ 電力損失の計算
P_loss = I² × R [W]
電力損失は電流の2乗に比例!
具体例:
電流I = 100A、抵抗R = 10Ω の送電線の場合
P_loss = 100² × 10 = 100,000W = 100kW の損失! 😱
💡 損失を減らす工夫
- ✅ 太い電線を使う(断面積Aを大きく)
- ✅ 高電圧・低電流で送電(I²に比例するため、Iを小さくすると効果的!)
- ✅ 抵抗率が低い銅やアルミを使う
🎯 これが「高圧送電」が使われる理由です!
電圧を10倍にして電流を1/10にすれば、損失は1/100に! 🎉
次の図で、抵抗の仕組みと損失の関係を詳しく見ていきましょう! 👇
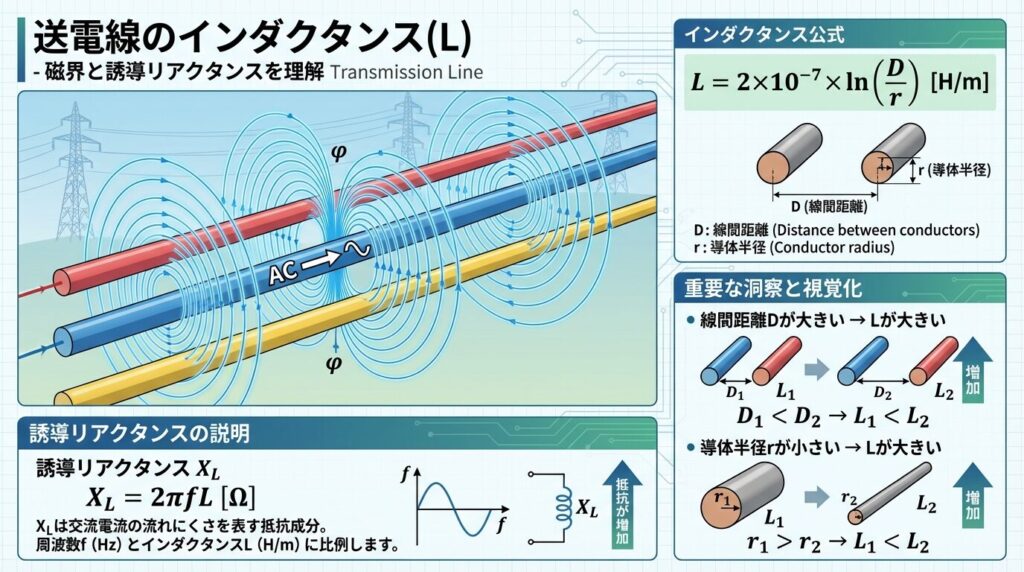
🧲 インダクタンス(L):磁界が生む電圧降下
送電線に交流電流が流れると、その周りに磁界が発生します。この磁界によって、インダクタンス(誘導性リアクタンス)が生じます。
📐 インダクタンスの計算式
L = 2×10⁻⁷ × ln(D/r) [H/m]
D:線間距離[m]、r:導体半径[m]
🔍 インダクタンスに影響する要素
① 線間距離D
距離が大きいほど、Lが大きくなる 📏
→ 電線間隔が広いと、磁界が広がりやすい
② 導体半径r
半径が小さいほど、Lが大きくなる
→ 細い電線は磁界が集中しやすい
⚡ 誘導リアクタンスの計算
XL = ωL = 2πfL [Ω/km]
f:周波数[Hz]、L:インダクタンス[H/km]
具体例:
周波数f = 60Hz、インダクタンスL = 1mH/km の場合
XL = 2π × 60 × 0.001 = 0.377Ω/km
📉 インダクタンスの影響
① 電圧降下が発生
V_drop = I × XL → 長距離送電では無視できない! 📉
② 電流が電圧より遅れる
力率が悪化(cosφ が小さくなる) 😱
→ 遅れ電流により、無効電力が増加
③ 無効電力の増加
実際に使える有効電力が減る → 送電効率が悪化
💡 インダクタンスを減らす工夫
- ✅ 多導体方式:1本の太い電線の代わりに、複数本の細い電線を束ねる
- ✅ 線間距離を小さく:ただし、短絡や放電のリスクとのトレードオフ
- ✅ 電力用コンデンサで力率改善(進み電流で遅れ電流を打ち消す)
次の図で、インダクタンスの仕組みと磁界の関係を確認しましょう! 👇
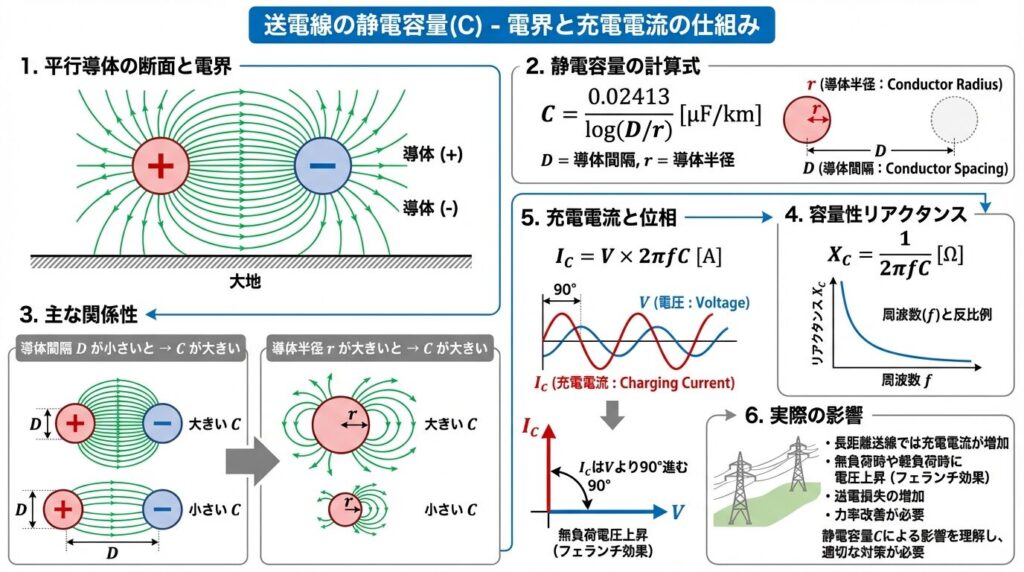
⚡ 静電容量(C):電界が生む充電電流
送電線の導体間には電界が発生し、あたかもコンデンサのように振る舞います。これが静電容量(C)です。
📐 静電容量の計算式
C = 0.02413 / log(D/r) [μF/km]
D:線間距離[m]、r:導体半径[m]
🔍 静電容量に影響する要素
① 線間距離D
距離が小さいほど、Cが大きくなる 📏
→ 電線が近いと、電界が強くなる
→ インダクタンスと逆の関係! 🔄
② 導体半径r
半径が大きいほど、Cが大きくなる
→ 太い電線は電荷を蓄えやすい
⚡ 容量性リアクタンスの計算
XC = 1/(ωC) = 1/(2πfC) [Ω・km]
周波数fが高いほど、XCは小さくなる(逆数!)
具体例:
周波数f = 60Hz、静電容量C = 0.01μF/km の場合
XC = 1/(2π × 60 × 0.01×10⁻⁶) = 265,000Ω・km = 265kΩ・km
💡 ポイント
XCは非常に大きい値(数百kΩ)なので、架空送電線では静電容量の影響は比較的小さいです。
ただし、地中ケーブルでは線間距離Dが小さいため、Cが数十倍になり、無視できません! ⚠️
📈 充電電流の発生
Ic = V × ωC = V × 2πfC [A]
電圧Vに比例した充電電流が流れる!
⚠️ 静電容量の影響
① 充電電流が常に流れる
負荷がゼロ(無負荷)でも、充電電流が流れる! 🔌
② フェランチ効果(受電端電圧上昇)
無負荷時に、受電端の電圧が送電端より高くなる現象 📈
→ 長距離送電では注意が必要!
③ 進み電流が流れる
電流が電圧より90°進む → インダクタンスと逆!
→ 場合によっては力率改善に役立つこともある ✨
💡 架空線 vs ケーブル
| 種類 | 線間距離D | 静電容量C |
|---|---|---|
| 架空送電線 | 大(数m) | 小(0.01μF/km程度) |
| 地中ケーブル | 小(数cm) | 大(0.3μF/km程度) 架空線の数十倍! |
次の図で、静電容量と充電電流の仕組みを詳しく見ていきましょう! 👇
✅ まとめ:3つの特性を理解して電験三種合格へ!
🎯 この記事のポイント
| 特性 | 原因 | 計算式 | 主な影響 |
|---|---|---|---|
| 抵抗(R) | 導体の抵抗 | R=ρl/A | 電力損失(I²R) |
| インダクタンス(L) | 磁界の発生 | L=2×10⁻⁷ln(D/r) | 電圧降下・遅れ電流 |
| 静電容量(C) | 電界の発生 | C=0.02413/log(D/r) | 充電電流・進み電流 |
💡 初心者向けの覚え方まとめ
- 🔥 抵抗R:熱が出る → 電力損失 → 太い線・高電圧で対策
- 🧲 インダクタンスL:磁界が出る → 電圧降下・遅れ電流 → 多導体・力率改善で対策
- ⚡ 静電容量C:電界が出る → 充電電流・進み電流 → ケーブルで特に大きい
📝 電験三種で頻出のポイント
- 📊 R、L、Cの計算式は必ず暗記!
- 📊 D(線間距離)とr(半径)の影響:Lは大きくなる、Cは小さくなる
- 📊 電力損失 = I²R:電流の2乗に比例(超重要!)
- 📊 XL = 2πfL、XC = 1/(2πfC):リアクタンスの計算
- 📊 フェランチ効果:無負荷時の電圧上昇(静電容量が原因)
- 📊 架空線 vs ケーブル:ケーブルはCが数十倍大きい
🎓 学習のコツ
- ✅ 水道管のアナロジーで理解:抵抗=摩擦、L=水の慣性、C=水槽
- ✅ 公式の意味を理解:長い・細い → Rが大きい、など
- ✅ 過去問で計算練習:数値を代入して何度も解く
- ✅ 3つの特性の相互関係:Dが大きい → L大・C小、など
📚 関連記事
🎉 この記事が役に立ったら、SNSでシェアしてくださいね!
一緒に電験三種合格を目指しましょう! 💪✨
