電験三種の勉強を始めると、必ず最初に出会うのがオームの法則 \( V=IR \) です。
「こんなの常識だよ」と思いましたか?
しかし、試験問題が複雑になった途端、式が立てられなくなる人が後を絶ちません。それは、この式を単なる記号の羅列として暗記しているからです。
今回は、目に見えない電気を「目に見える水路」に置き換えて、オームの法則の本質を脳にインストールします。
目次
1. 電気回路と水路は「全く同じ」だ!
電気回路図を見ると頭が痛くなる人は、まずこの「翻訳」を頭に入れてください。
電気の流れは、実は水の流れ(ポンプとパイプ)と全く同じ仕組みで動いています。
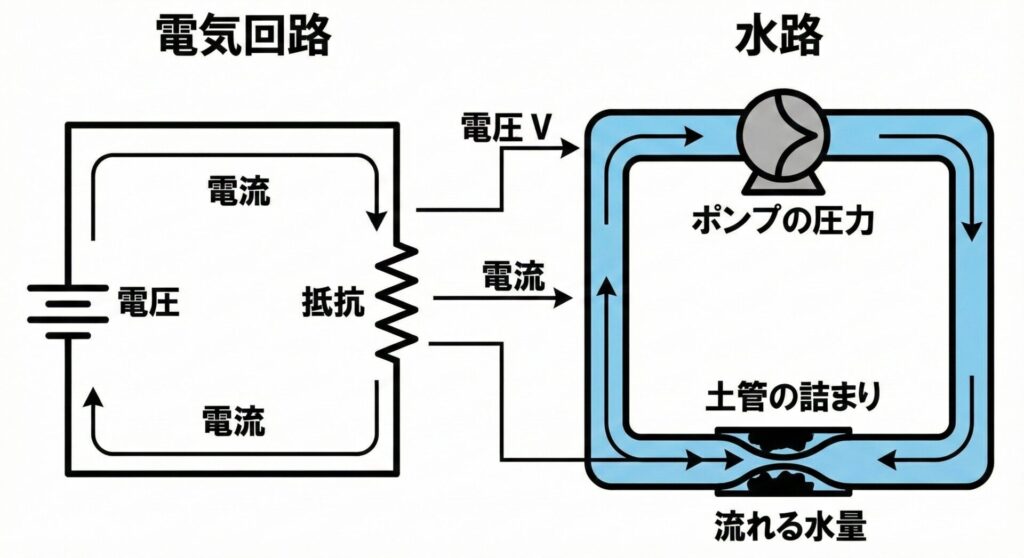
| 電気の世界 | 水路の世界 | 役割・イメージ |
|---|---|---|
| 電圧 \( V \) [V] ボルト |
🌊 ポンプの圧力 |
水を押し出す「強さ」。 水圧や高低差。 |
| 電流 \( I \) [A] アンペア |
💧 流れる水量 |
実際に流れている「水の量」。 結果として発生するもの。 |
| 抵抗 \( R \) [Ω] オーム |
🚧 土管の詰まり |
流れを邪魔する「障害物」。 パイプの細さや、中のゴミ。 |
2. 電圧(ポンプ)と電流(水流)の関係
まずは、障害物(抵抗)が決まっている状態で、ポンプの力を変えてみましょう。
想像してください。ポンプのスイッチを強くして、水圧(電圧 \(V\))を2倍に上げたとします。
すると、押し出される水の量(電流 \(I\))はどうなるでしょうか?
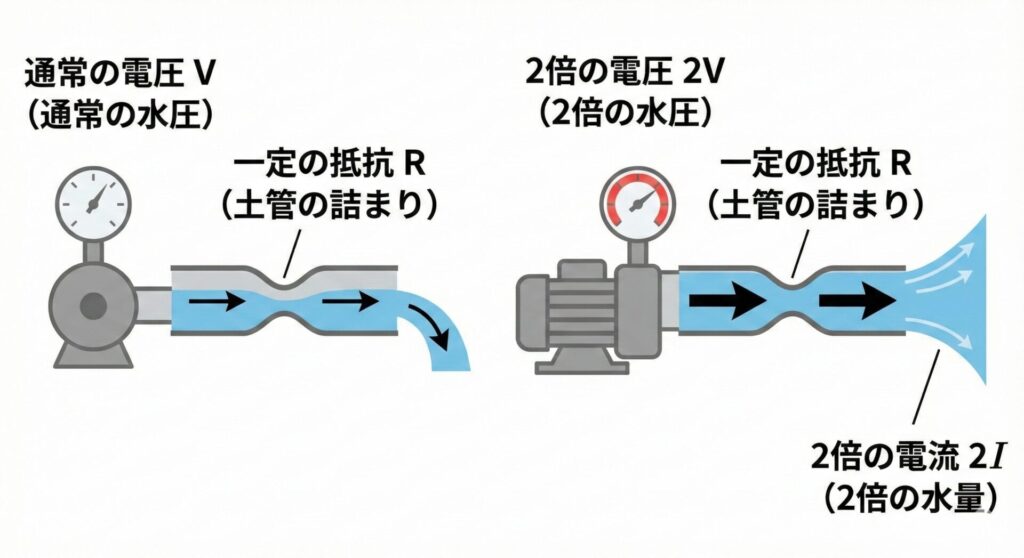
当然、水は勢いよく流れ出し、流れる量も2倍になります。
これが「電流は電圧に比例する(\( I \propto V \))」という意味です。
3. 抵抗(土管の詰まり)の正体
次に、ポンプの力(電圧)はそのままにして、通り道であるパイプを変えてみます。
パイプの中にゴミが詰まっていたり、パイプ自体が極端に細かったりしたらどうでしょう?
これが「電気抵抗 \(R\)」です。
通り道が狭くなればなるほど(抵抗 \(R\) が大きくなるほど)、水は流れにくくなります。
もし抵抗が2倍流にくいパイプになったら、流れる水(電流)は半分(1/2)になってしまいます。
「電流 \(I\)」は、あくまで「結果」です。
「電圧 \(V\)(押す力)」と「抵抗 \(R\)(邪魔する要素)」の力関係によって、結果的にどれだけの「電流 \(I\)(水)」が流れるかが決まります。
4. 結論:なぜ V = IR なのか?
以上のイメージを数式にまとめると、オームの法則の真の意味が見えてきます。
① 電流を求めたいとき( \( I = V / R \) )
「どれだけ水が流れるか(\(I\))?」は、「押す力(\(V\))」を「邪魔する力(\(R\))」で割ればわかります。
- 押す力が強い(分子が大きい) → たくさん流れる
- 邪魔が大きい(分母が大きい) → チョロチョロしか流れない
② 電圧降下を知りたいとき( \( V = I \times R \) )
これは少し見方を変えます。「ある抵抗(\(R\))に、無理やりこれだけの電流(\(I\))を流すためには、どれだけの圧力(\(V\))が必要か?」と考えます。
必要な圧力(V) = 流したい量(I) × 通りにくさ(R)
通りにくい細い管(大きな \(R\))に、大量の水(大きな \(I\))を流そうとしたら、ものすごい圧力(大きな \(V\))が必要になりますよね。
これが \( V=IR \) の物理的な意味です。
まとめ:数式を図で翻訳しよう
オームの法則は、記号の暗記ではなく「ポンプ・水流・土管」の紙芝居として頭に入れておきましょう。
このイメージさえあれば、この先に登場する「直列・並列回路」や「キルヒホッフの法則」も、すべて水の流れとして直感的に解けるようになります。
