💡 こんな悩みを抱えていませんか?
✅ 「交流って直流と何が違うの?」
✅ 「正弦波・周波数・周期…専門用語が多すぎて混乱!」
✅ 「公式の暗記ばかりでイメージが湧かない…」
→ 安心してください。この記事で「交流の本質」が完全にイメージできるようになります。
目次
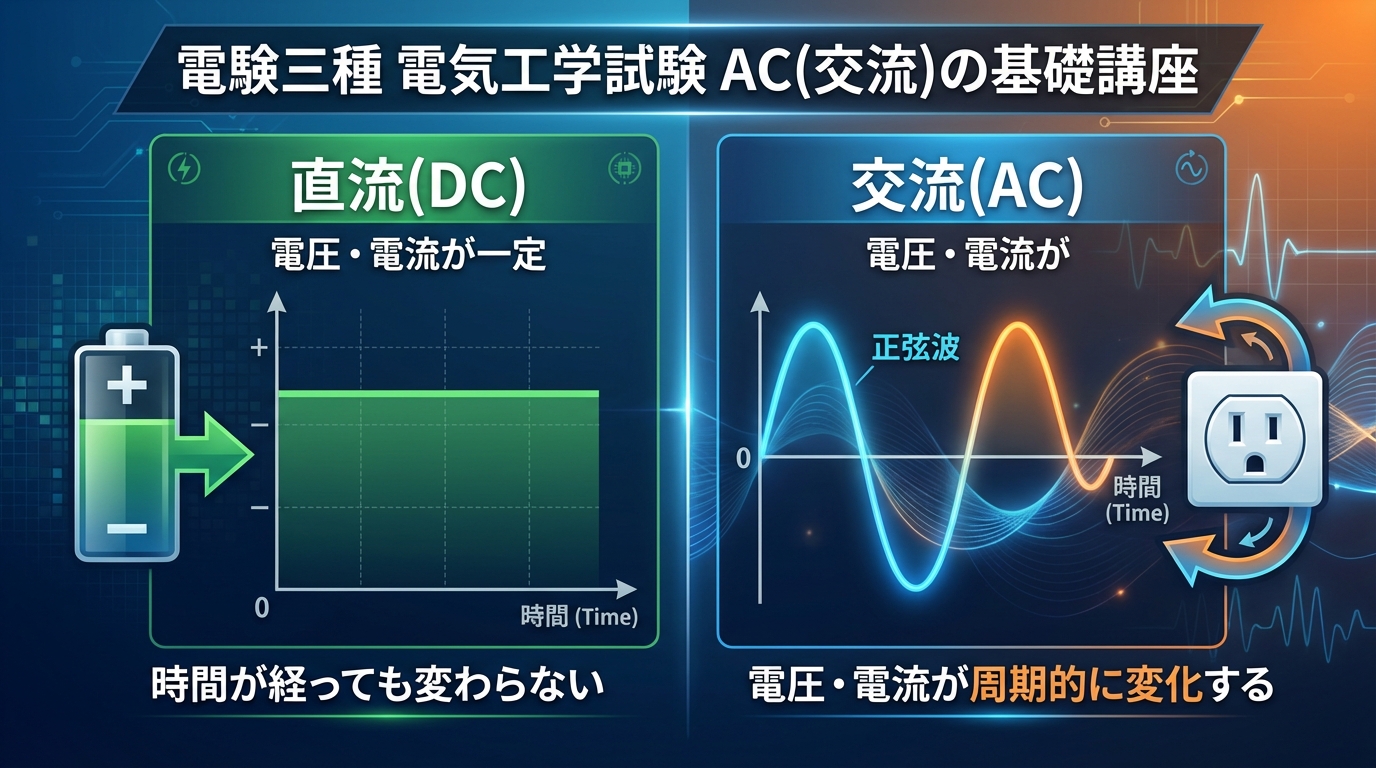
⚡ 交流(AC)とは?|直流(DC)との決定的な違い
結論から言うと、交流とは「電圧・電流の大きさと向きが周期的に変化する電気」のことです。
一方、直流(DC)は乾電池のように、電圧・電流の大きさと向きが常に一定です。
例えば、コンセントから供給される家庭用電源は交流(AC 100V、周波数50Hzまたは60Hz)です。
電池で動くスマホの内部は直流(DC)ですよね。
📌 覚えるべき定義
直流(DC: Direct Current)
→ 電圧・電流の大きさと向きが常に一定
交流(AC: Alternating Current)
→ 電圧・電流の大きさと向きが周期的に変化
🔄 交流の「変化する」とは?
「変化する」とは、プラス・マイナスを繰り返すということです。
直流では電流が一方向にしか流れませんが、交流では正方向→ゼロ→負方向→ゼロを繰り返します。
これがいわゆる「振動(oscillation)」です。
この振動の仕方を表す代表的な波形が正弦波(sine wave)です。次の章で詳しく見ていきましょう。
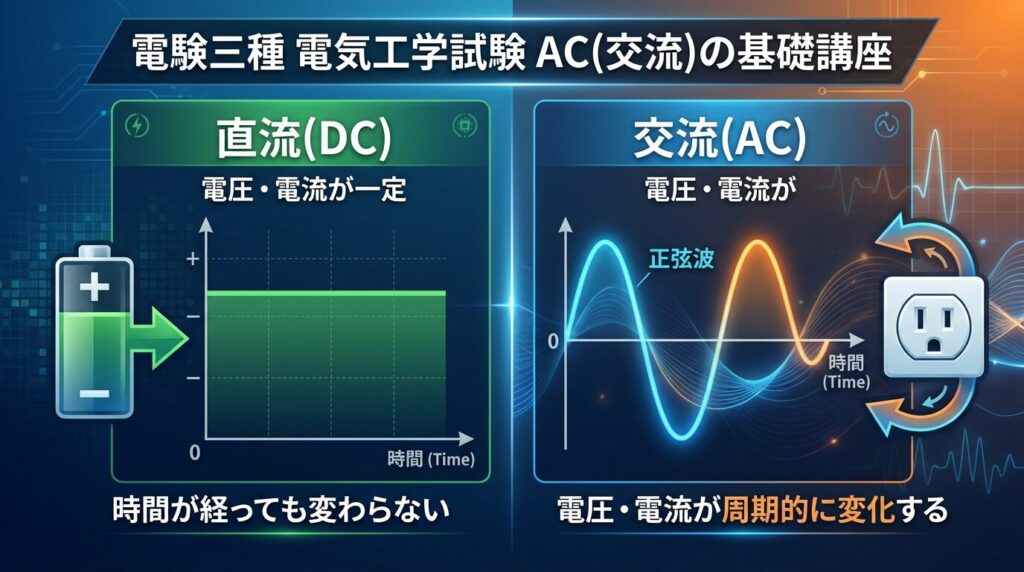
📈 正弦波交流とは?|なぜ「サイン(sin)」なのか?
交流の波形にはいくつか種類がありますが、電験三種で最も頻出するのが正弦波交流です。
正弦波は、数学の三角関数「sin(サイン)」で表現できる波形で、なめらかな曲線が特徴です。
家庭用電源など、実用上の交流はほぼすべて正弦波交流です。
📐 正弦波交流の瞬時値の式
v = Vm sin(ωt)
i = Im sin(ωt)
※ Vm、Imは最大値、ωは角周波数、tは時間
🎢 ブランコの比喩で理解する正弦波
正弦波交流を理解するには、「ブランコ」のイメージが最適です。
ブランコは、前→中央→後ろ→中央→前と、規則正しく振動しますよね?
この動きが、まさに正弦波そのものなんです。
- ブランコが最も高い位置 → 電圧・電流が最大値
- ブランコが中央を通過 → 電圧・電流がゼロ
- 前後の往復 → 電圧・電流の正負の変化
- 1往復にかかる時間 → 周期T
この「ブランコの動き」を横軸に時間、縦軸に変位(電圧・電流)で描くと、なめらかな波形ができあがります。
これが正弦波です。
🌊 正弦波の重要な値
正弦波には、試験で頻出する3つの重要な値があります。
このうち、試験で最も重要なのは「実効値」です。
家庭用電源の「AC 100V」も、この実効値を指しています。
実効値とは、「交流が直流と同じ仕事をするときの値」と考えるとイメージしやすいです。
📝 電験三種では「実効値の計算」が頻出するので、まずはV = Vm/√2の公式を必ず覚えてください。
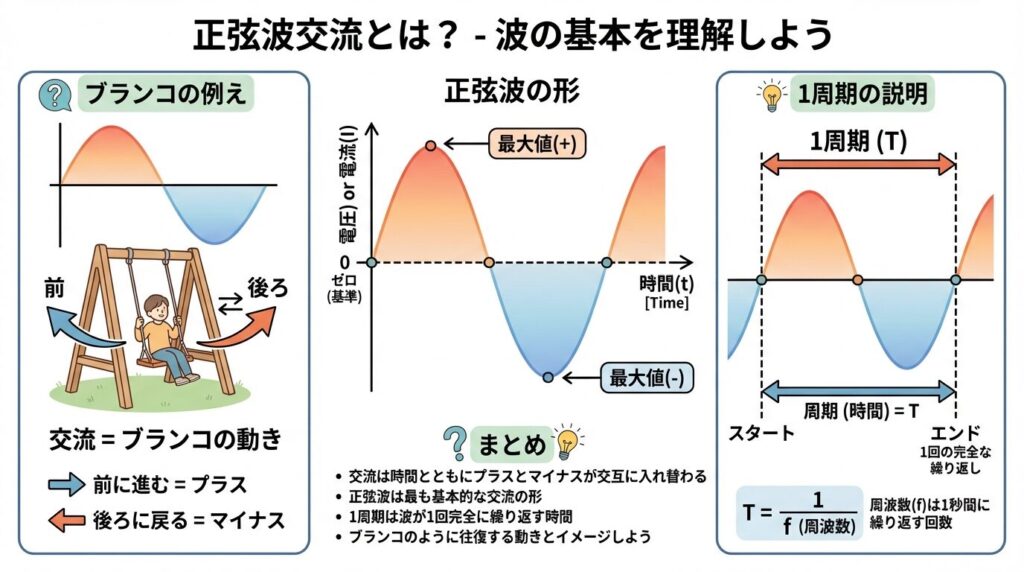
🔁 周波数f・周期T・角周波数ω|3つの関係を完全理解
交流を理解するうえで絶対に避けて通れないのが、周波数f・周期T・角周波数ωの3つです。
これらはすべて繋がっているので、まとめて理解することが重要です。
⏱️ 周期T(Period)とは?
周期Tとは、1回の振動にかかる時間のことです。
単位は秒(s)です。
ブランコで言えば、「前→後ろ→前」と1往復するのにかかる時間が周期Tです。
例えば、日本の東日本の電源周波数は50Hzです。
これは「1秒間に50回振動する」という意味なので、
T = 1/f = 1/50 = 0.02秒(=20ms)
つまり、1回の振動に0.02秒かかるということです。
📊 周波数f(Frequency)とは?
周波数fとは、1秒間に繰り返される振動の回数のことです。
単位はヘルツ(Hz)です。
周期Tと周波数fは逆数の関係にあります。
📐 周波数と周期の関係式
f = 1/T
T = 1/f
- 周波数が高い → 周期が短い → 振動が速い
- 周波数が低い → 周期が長い → 振動がゆっくり
日本の電源周波数は東日本50Hz、西日本60Hzと覚えておきましょう。
電験三種では、この値を使った計算問題がよく出題されます。
🔄 角周波数ω(Angular Frequency)とは?
角周波数ωは、1秒間に回転する角度を表します。
単位はラジアン毎秒(rad/s)です。
周波数fとの関係は以下の式で表されます。
📐 角周波数の公式
ω = 2πf = 2π/T
※ π(パイ) ≒ 3.14
角周波数は、回転運動と関連づけて覚えると理解しやすいです。
交流の正弦波は、円運動を横から見た「投影」として表現できるからです。
📝 より詳しい内容は、「角周波数ωの意味と計算」の記事で解説しています。
🧠 3つの関係をまとめて整理
🎯 3つの関係式を一気に覚える!
f = 1/T
ω = 2πf = 2π/T
この2式さえ覚えれば、どんな問題にも対応できます。
📝 交流の計算問題|試験でよく出るパターンと解き方
ここまで学んだ内容を、実際の計算問題で使ってみましょう。
電験三種では、以下のような問題が頻出します。
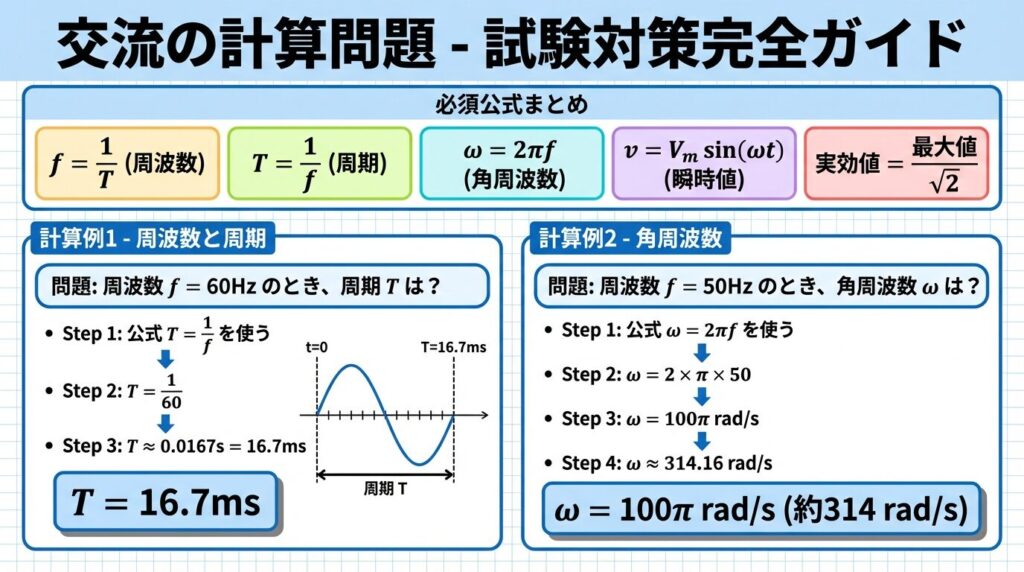
📘 例題1|周波数から周期を求める
【問題】
周波数60Hzの交流の周期Tを求めよ。
【解答】
公式 T = 1/f を使います。
T = 1/60 ≒ 0.0167秒(約16.7ms)
60Hzの交流は、1回の振動に約0.0167秒かかるということですね。
📘 例題2|角周波数を求める
【問題】
周波数50Hzの交流の角周波数ωを求めよ。
(ただし、π=3.14とする)
【解答】
公式 ω = 2πf を使います。
ω = 2 × 3.14 × 50 = 314 rad/s
角周波数は314 rad/sです。
この値も試験でよく出るので、50Hz → 314 rad/sと覚えておくと便利です。
📘 例題3|最大値から実効値を求める
【問題】
最大値Vm=141Vの正弦波交流の実効値Vを求めよ。
(√2 = 1.414とする)
【解答】
公式 V = Vm/√2 を使います。
V = 141 / 1.414 ≒ 100V
実効値は100Vです。
これが、家庭用コンセントの「AC 100V」の正体です!
⚠️ よくあるミスと対策
🎯 試験で覚えるべき数値
- 日本の電源周波数: 東日本50Hz、西日本60Hz
- 実効値の係数: V = Vm/√2 ≒ 0.707Vm
- 平均値の係数: Vav = 2Vm/π ≒ 0.637Vm
- 角周波数の計算: 50Hz → ω≒314 rad/s、60Hz → ω≒377 rad/s
- √2の値: 1.414(問題文に記載があれば従う)
📝 さらに詳しい計算問題は、「電力と電力量の違い」の記事でも解説しています。
✅ まとめ|交流の基本をもう一度整理
お疲れ様でした!
この記事では、交流の基本中の基本である「正弦波・周波数・周期・角周波数」を解説しました。
🎯 この記事で押さえるべきポイント
- 交流とは: 電圧・電流が周期的に変化する電気
- 正弦波: なめらかな波形。家庭用電源はこれ。
- 実効値: V = Vm/√2(試験最頻出!)
- 周波数f: 1秒間に繰り返す回数(Hz)
- 周期T: 1回の振動にかかる時間(s)
- 角周波数ω: ω = 2πf(回転角度/秒)
- 3つの関係式: f = 1/T、ω = 2πf
📚 次のステップ|合格への学習法
交流の基本を理解したら、次は以下のテーマに進みましょう。
- リアクタンス(XL、XC) → インピーダンスの理解に必須
- インピーダンス(Z) → 交流回路の抵抗
- 複素数表示 → ベクトル図と計算
- 共振回路 → RLC回路の応用
これらのテーマも、ブランコの比喩やイメージ重視で丁寧に解説していきます。
まずは今回の内容を完璧に理解してから、次へ進んでくださいね。
🔗 あわせて読みたい関連記事
🎓 最後に|応援メッセージ
交流は最初こそ難しく感じますが、イメージで理解すれば必ず突破できます。
「ブランコの動き=正弦波」「周波数=振動の速さ」というイメージを大切に、計算練習を重ねていきましょう。
あなたの合格を心から応援しています! 💪🔥