💡 この記事でわかること
- リアクタンス(X)とは何か、抵抗(R)との違い
- 誘導性リアクタンス(XL)の式と周波数特性
- 容量性リアクタンス(XC)の式と周波数特性
- 周波数が変わると回路がどう変化するか(イメージで理解)
- 電験三種で出題されるポイントと計算例
電験三種の「理論」科目で必ず登場するリアクタンス。
「抵抗(R)はわかるけど、XLとXCって何?」と感じる方が多いのではないでしょうか。
実は、リアクタンスは「周波数によって変わる交流回路の抵抗成分」のこと。
コイル(L)やコンデンサ(C)が持つ、「電流を妨げる力」なんです。
この記事では、中学生にもわかるように、具体例・図解・比喩を使って、リアクタンスの正体を徹底解説します!
📌 今回のゴール
① リアクタンス(XL・XC)の意味がイメージできる
② 周波数fが変わるとXL・XCがどう変化するか理解できる
③ 電験三種の計算問題が解けるようになる
目次
🔌 リアクタンス(X)とは?|交流回路の「見えない抵抗」
🧱 まずは「抵抗(R)」のおさらい
抵抗(R)は、電流を妨げる部品です。
直流(DC)でも交流(AC)でも、同じように電流を妨げます。
💡 抵抗のイメージ
水道管の中に「砂利」を詰めると、水(電流)が流れにくくなりますよね。
これが抵抗(R)です。
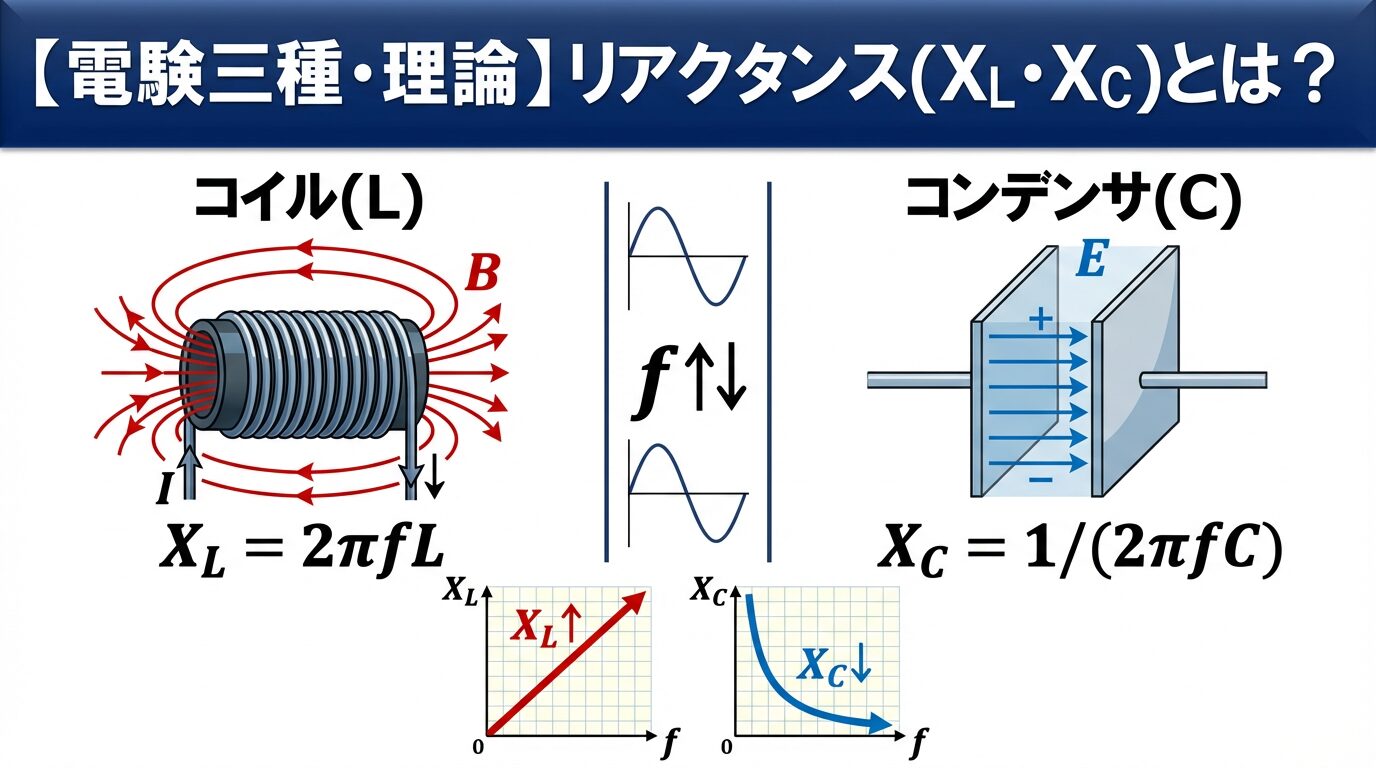
⚡ リアクタンス(X)とは?
一方、リアクタンス(X)は、交流回路だけに現れる「見えない抵抗」です。
リアクタンスは、コイル(L)やコンデンサ(C)が持つ性質で、周波数(f)によって値が変わるのが最大の特徴です。
📘 リアクタンスの2つの種類
① 誘導性リアクタンス(XL) … コイル(L)が持つ交流抵抗
② 容量性リアクタンス(XC) … コンデンサ(C)が持つ交流抵抗
🌀 なぜ「周波数で変わる」のか?
コイルやコンデンサは、電流の変化に反応する部品です。
交流は周波数(f)が高いほど電流の変化が激しいため、コイルやコンデンサの「反応の仕方」が変わります。
💡 イメージ例
自転車のペダルを速く漕ぐ(高周波)と、タイヤの抵抗が大きく感じられますよね。
ゆっくり漕ぐ(低周波)と、抵抗は小さく感じます。
リアクタンスも、周波数によって「抵抗感」が変わるのです。
それでは、XLとXCの具体的な式と特徴を見ていきましょう!
🌀 誘導性リアクタンス(XL)|コイルの交流抵抗
📐 誘導性リアクタンスの公式
誘導性リアクタンス(XL)
XL = ωL = 2πfL
📌 記号の意味
- XL … 誘導性リアクタンス [Ω]
- ω(オメガ) … 角周波数 [rad/s](ω = 2πf)
- f … 周波数 [Hz]
- L … インダクタンス(コイルの大きさ) [H]
- π(パイ) … 円周率(約3.14)
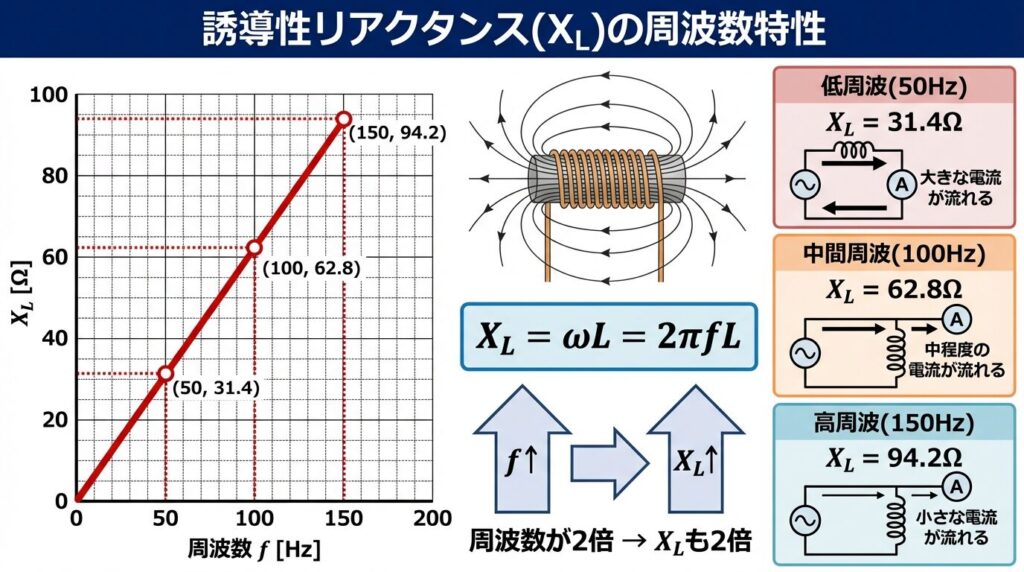
📈 周波数が上がると、XLも上がる!
式を見ると、XL = 2πfLなので、周波数(f)が大きくなると、XLも大きくなることがわかります。
💡 イメージ例
コイルは「電流の変化を嫌う」性質があります。
周波数が高い(電流の変化が激しい)ほど、コイルは「変化を妨げようとする力」を強くします。
つまり、高周波ほど、コイルは電流を妨げる(XLが大きくなる)のです。
🔢 具体例で計算してみよう
📝 問題
インダクタンス L = 0.1 H のコイルに、周波数 f = 50 Hz の交流を流したとき、誘導性リアクタンス XL はいくらか?
✅ 解答
XL = 2πfL
= 2 × 3.14 × 50 × 0.1
= 31.4 Ω
もし周波数を f = 100 Hz にすると、XL = 62.8 Ωになり、周波数が2倍になるとXLも2倍になることがわかります。
📌 まとめ
✅ 誘導性リアクタンス(XL)は、周波数(f)に比例して大きくなる
✅ 高周波ほど、コイルは電流を妨げる力が強い
✅ 公式は XL = 2πfL
⚡ 容量性リアクタンス(XC)|コンデンサの交流抵抗
📐 容量性リアクタンスの公式
容量性リアクタンス(XC)
XC = 1 / (ωC) = 1 / (2πfC)
📌 記号の意味
- XC … 容量性リアクタンス [Ω]
- ω(オメガ) … 角周波数 [rad/s](ω = 2πf)
- f … 周波数 [Hz]
- C … 静電容量(コンデンサの大きさ) [F]
- π(パイ) … 円周率(約3.14)
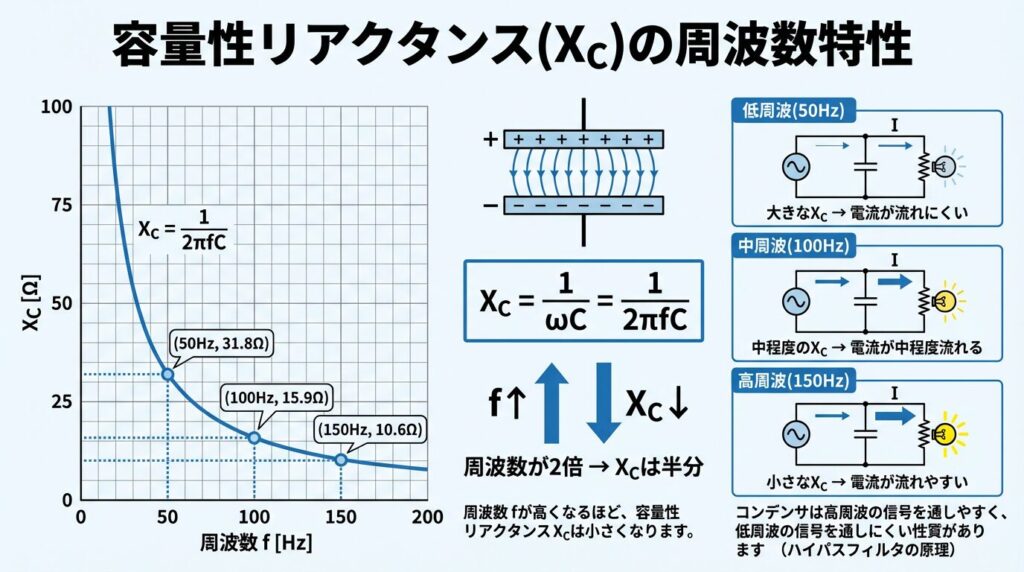
📉 周波数が上がると、XCは下がる!
式を見ると、XC = 1 / (2πfC)なので、周波数(f)が大きくなると、XCは小さくなることがわかります。
💡 イメージ例
コンデンサは「電荷を溜める」部品ですが、交流では「充電と放電を繰り返す」動作をします。
周波数が高い(切り替わりが速い)ほど、コンデンサは「充放電が追いつかず、電流が流れやすくなる」のです。
つまり、高周波ほど、コンデンサは電流を妨げない(XCが小さくなる)のです。
🔢 具体例で計算してみよう
📝 問題
静電容量 C = 100 μF のコンデンサに、周波数 f = 50 Hz の交流を流したとき、容量性リアクタンス XC はいくらか?
✅ 解答
XC = 1 / (2πfC)
= 1 / (2 × 3.14 × 50 × 100 × 10-6)
= 31.8 Ω
もし周波数を f = 100 Hz にすると、XC = 15.9 Ωになり、周波数が2倍になるとXCは半分になることがわかります。
📌 まとめ
✅ 容量性リアクタンス(XC)は、周波数(f)に反比例して小さくなる
✅ 高周波ほど、コンデンサは電流を通しやすい
✅ 公式は XC = 1 / (2πfC)
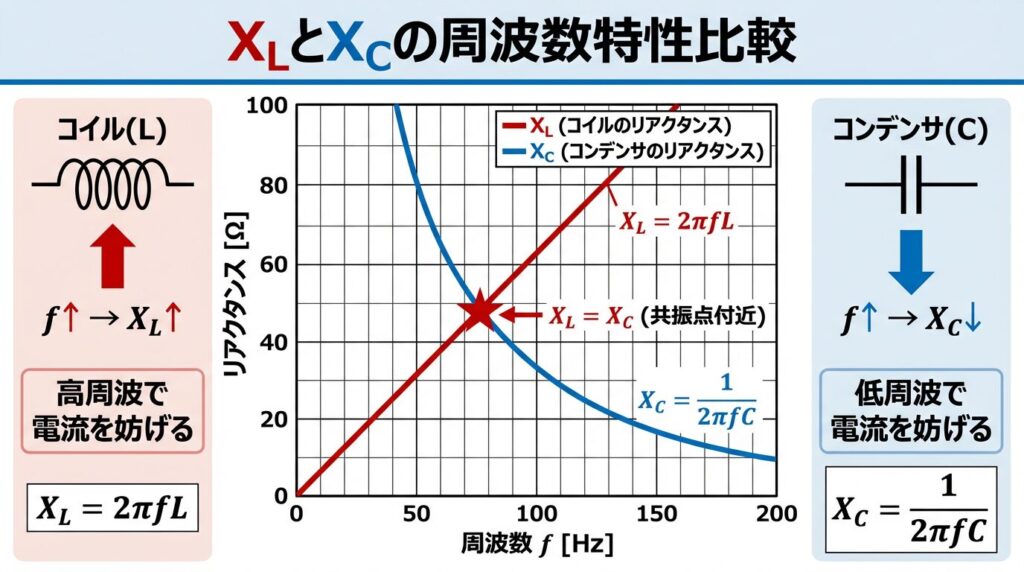
🔄 XLとXCの違いまとめ|周波数特性を比較
💡 覚え方のコツ
✅ コイル(L)は「高周波が苦手」→ 高周波ほど XL が大きくなる
✅ コンデンサ(C)は「高周波が得意」→ 高周波ほど XC が小さくなる
✅ 直流のとき、コイルは「ただの導線」、コンデンサは「絶縁体」
✅ まとめ|リアクタンス(XL・XC)の重要ポイント
📌 今日学んだこと
- リアクタンス(X)は、交流回路だけに現れる「見えない抵抗」
- 誘導性リアクタンス(XL)は、コイルが持つ交流抵抗
- XL = 2πfL で、周波数(f)が上がるとXLも上がる
- 容量性リアクタンス(XC)は、コンデンサが持つ交流抵抗
- XC = 1/(2πfC) で、周波数(f)が上がるとXCは下がる
- 直流(f=0)のとき、コイルは短絡、コンデンサは開放
🚀 次のステップ|さらに理解を深めよう
リアクタンスの概念が理解できたら、次はインピーダンス(Z)を学びましょう!
インピーダンスは、抵抗(R)とリアクタンス(X)を合成したもので、交流回路の総合的な抵抗です。
交流回路の全体像を理解しよう ⚡ R-L-C素子の性質|抵抗・コイル・コンデンサの交流特性
コイルとコンデンサの基礎を復習 📊 交流の瞬時値と位相|sinωtを完全理解
位相とリアクタンスの関係を深掘り
🎓 電験三種の合格を目指すあなたへ
この記事が「わかった!」と思えたら、次の単元へ進みましょう。
一つ一つ着実に理解を積み重ねることが、合格への最短ルートです。
あなたなら必ずできます! 💪✨
最後まで読んでいただき、ありがとうございました!
質問や感想があれば、お気軽にコメントください 😊