💡 こんな実験で困っていませんか？
✅「機械の設定変更は1日がかり…でも温度は簡単に変えられる。どう実験すれば効率的？」
✅「大きな単位の因子と小さな単位の因子が混在していて、実験計画が立てにくい」
✅「分割法（スプリットプロット法）って聞いたことあるけど、何が違うの？」
🎯 この記事を読むとわかること
✔ 分割法（スプリットプロット法）とは何か？
✔ なぜ「変えにくい因子」と「変えやすい因子」を分ける必要があるのか
✔ 主プロット・副プロットの考え方と具体例
✔ 分割法を使う際の注意点と解析のポイント
目次
🌟 はじめに：すべての因子を同じように扱えない実験がある
これまで「実験計画法」で学んできた設計法では、
- 🔹 因子間の主効果や交互作用を調べる
- 🔹 ばらつきをコントロールするためにブロック（局所管理）を使う
という方法で実験を組み立ててきました。
しかし、実際の現場では、すべての因子を「同じ自由度」で扱えるとは限りません。
🔥 現場でよくあるジレンマ
🏭 機械の設定変更：1回変えるのに半日～1日かかる（変えにくい因子）
🌡️ 温度や時間の調整：数分で簡単に変えられる（変えやすい因子）
💸 すべての組み合わせを完全ランダムに実験したら、コストが爆発する…
このように「大きな単位でしか設定できない因子」と「小さな単位で自由に設定できる因子」が混在する場合、特別な設計法が必要になります。
それが分割法（スプリットプロット法）です！
📘 1. 分割法とは？
定義をシンプルに理解する
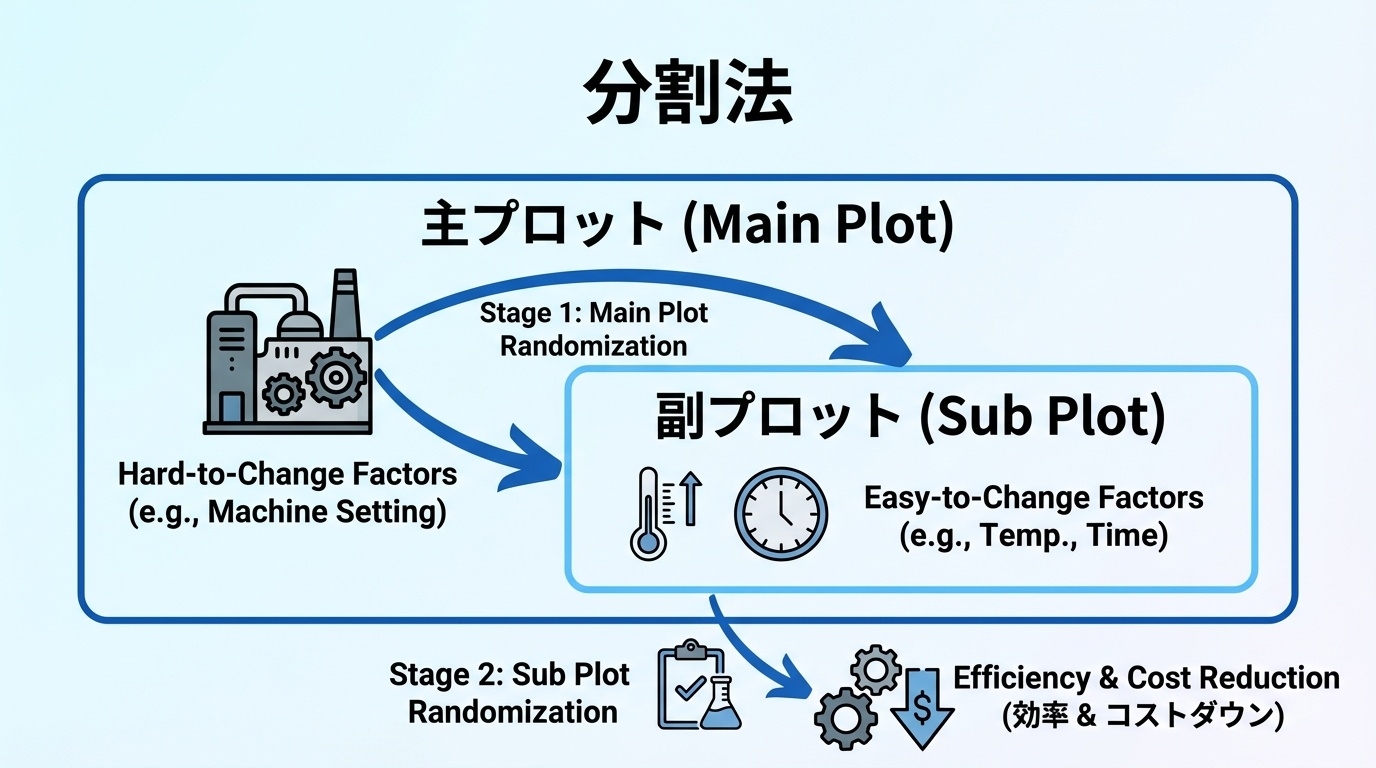
💡 分割法（スプリットプロット法）とは
大きな単位（粗い条件）と小さな単位（細かい条件）の両方を効率的に実験できるように、2段階で割り付けを行う設計法のことです。
つまり、
- 🔹 粗い因子（変えにくい因子）：主プロット（Main Plot）
- 🔹 細かい因子（簡単に変えられる因子）：副プロット（Sub Plot）
の2つに分けて考える方法です。
他の実験計画法との違い
| 設計法 | ランダム化の範囲 | 適用場面 |
|---|---|---|
| 一元配置実験 | 全実験で完全ランダム化 | 因子1つを調べる単純な実験 |
| 二元配置実験 | 全実験で完全ランダム化 | 2因子を同等に扱える実験 |
| 分割法 | 2段階でランダム化（主→副） | 因子によって変更コストが大きく異なる実験 |
👉 フィッシャーの三原則の「ランダム化」を2段階に分けて適用するのが分割法の本質です。
🔥 2. なぜ分割法が必要なのか？
すべての因子を完全ランダム化すると非効率になる
通常のランダム化では、「すべての実験順序を完全にシャッフルする」のが理想です。
しかし、以下のような場合、完全ランダム化は現実的ではありません。
❌ 完全ランダム化が非効率な例
【製造ライン実験】
🏭 因子A：機械の型番（変更に6時間かかる）
🌡️ 因子B：加熱温度（変更に5分）
→ 完全ランダムに実験すると、機械を何度も交換することになり、準備時間だけで何日もかかる…
✅ 分割法を使うと効率的
1. まず機械Aで全温度パターンを試す（主プロット固定）
2. 次に機械Bに切り替えて、同じく全温度パターンを試す
→ 機械交換は1回だけで済む！大幅な時間短縮が可能
つまり、変えにくい因子はまとめて扱い、変えやすい因子は小分けで試すことで、現場の実験を現実的なコストで実施できるのです！
👉 因子と水準の性質を理解すると、どの因子を主プロット・副プロットに割り当てるべきかが判断できるようになります。
📊 3. 分割法の基本構成
主プロット（Main Plot）と副プロット（Sub Plot）
🟢 分割法の構造
【主プロット（Main Plot）】
🔹 変えにくい因子を割り当てる（例：機械の種類、炉の番号）
🔹 大きな実験単位を形成する
🔹 主プロット内で副プロットの実験を行う
【副プロット（Sub Plot）】
🔹 変えやすい因子を割り当てる（例：温度、時間、材料の量）
🔹 主プロットの中で細かく変更して試す
🔹 副プロット間はランダム化される
イメージ図で理解する
📐 分割法の構造イメージ
🏭 主プロット1：機械A
🌡️ 副プロット1-1：温度50℃
🌡️ 副プロット1-2：温度70℃
🌡️ 副プロット1-3：温度90℃
🏭 主プロット2：機械B
🌡️ 副プロット2-1：温度50℃
🌡️ 副プロット2-2：温度70℃
🌡️ 副プロット2-3：温度90℃
→ 主プロット（機械）を固定して、その中で副プロット（温度）を試すイメージ！
👉 繰返しの概念も分割法では重要です。主プロットの繰返しと副プロットの繰返しは別々に考えます。
🍛 4. 具体例：カレーの味評価で考える
実験の設定
たとえば、「美味しいカレーを作る実験」で以下の2つの因子を調べたいとします。
🍛 カレー実験の設定
【主プロット因子】
🍳 調理器具：鍋A、鍋B（交換するのが大変）
【副プロット因子】
🌶️ スパイス量：少なめ、多め（簡単に変えられる）
分割法での実験手順
✅ ステップ1：主プロットを設定
🍳 まず鍋Aを準備する
✅ ステップ2：副プロットの実験（鍋A固定）
🌶️ 鍋Aで「スパイス少なめ」のカレーを作る
🌶️ 鍋Aで「スパイス多め」のカレーを作る
✅ ステップ3：主プロットを変更
🍳 鍋Bに交換する
✅ ステップ4：副プロットの実験（鍋B固定）
🌶️ 鍋Bで「スパイス少なめ」のカレーを作る
🌶️ 鍋Bで「スパイス多め」のカレーを作る
💡 分割法のメリット
🔹 鍋の交換は1回だけで済む（完全ランダムなら何度も交換が必要）
🔹 スパイス量の変更は各鍋ごとに自由に試せる
🔹 効率的かつ現実的な実験計画になる
👉 鍋とスパイス量の交互作用も分割法で推定できます。
⚠️ 5. 分割法の注意点
注意点1：主プロットと副プロットで誤差構造が異なる
⚠️ 誤差が2種類ある
🔹 主プロット誤差：主プロット間のばらつき（大きい）
🔹 副プロット誤差：副プロット間のばらつき（小さい）
→ 分散分析では、この2つの誤差を別々に計算する必要があります
👉 自由度の考え方を理解すると、分割法の分散分析表が読めるようになります。
注意点2：主プロットの検出力は低くなる
注意点3：完全ランダム化より制約がある
⚠️ 完全ランダム化ではない
分割法は「制約付きランダム化」のため、完全ランダム化に比べて統計的な効率が若干下がります。
→ しかし現実的なコスト削減効果を考えれば、トレードオフとして十分に価値があります
👉 交絡の恐怖を理解すると、分割法でも因子の割り付けミスを防げます。
注意点4：解析にはソフトウェアの活用が必須
分割法の分散分析は手計算では非常に大変です。MinitabやJMP、Rなどの統計ソフトウェアを活用しましょう。
👉 実験計画法まとめ+確認問題で分割法の知識を整理できます。
📝 まとめ
✅ この記事のポイント
🔹 分割法は、「変えにくい因子」と「変えやすい因子」を分けて扱う実験設計
🔹 主プロット因子（粗い単位）と副プロット因子（細かい単位）に区別して割り付ける
🔹 現場の実験（設備変更・条件変更が混在する場合）で非常に重要なテクニック
🔹 主プロットと副プロットで誤差構造が異なるため、解析には注意が必要
🚀 次の記事へ
📖 次はこちらの記事がおすすめ！
分割法で効率的な実験設計を学んだ次は、「最適条件を探し出す方法」を学びましょう。
👉 次の記事：応答曲面法とは？山の頂上を見つける実験設計
🔹 応答曲面法を理解すると、「もっと良い条件（ベストな設定）」を科学的に探し出す力が身につきます！
📚 実験計画法の「挫折」を救う2冊
「数式を見た瞬間に本を閉じた」
そんな経験がある私だからこそ推せる、厳選のバイブルです。
