📌 この記事はこんな人におすすめ
- 「分散分析」という言葉を聞いたけど、何のことかわからない
- なぜ「平均の差」ではなく「分散」を分析するのか疑問
- 実験計画法を学び始めたけど、最初でつまずいている
- QC検定や電験三種で分散分析が出てきて困っている
「分散分析」って、名前からして難しそうですよね。
「分散」を「分析」する?
平均値を比べればいいんじゃないの?
なんでわざわざ「バラつき」を調べるの?
私も最初は同じ疑問を持っていました。
でも、ある例を知ったとき、「なるほど、だから分散を見るのか!」とスッキリ理解できたんです。
💡 結論から言うと
分散分析とは、「平均値の差が、本当に意味のある差なのか?それとも偶然のバラつきなのか?」を判定する方法です。
平均値だけを見ても、「たまたま」なのか「本当の差」なのかわからない。
だから「バラつき(分散)」を分析して、真実を見抜くのです。
目次
まずは「平均値だけ見る」の落とし穴を体験しよう
分散分析の必要性を理解するために、まずは「平均値だけを見ると、どう間違えるか」を体験してみましょう。
【実験】3種類のコーヒー豆、どれが一番おいしい?
あなたはカフェのオーナーです。
3種類のコーヒー豆(A、B、C)のどれを採用するか決めるために、お客さん5人に味を評価してもらいました。
評価は10点満点です。
☕ 実験1の結果
| 豆の種類 | 1人目 | 2人目 | 3人目 | 4人目 | 5人目 | 平均 |
|---|---|---|---|---|---|---|
| 豆A | 6 | 7 | 6 | 7 | 4 | 6.0 |
| 豆B | 7 | 8 | 7 | 8 | 5 | 7.0 |
| 豆C | 8 | 9 | 8 | 9 | 6 | 8.0 |
平均値を見ると、豆C(8.0点)が一番高いですね。
「よし、豆Cに決めた!」と言いたくなります。
でも、ちょっと待ってください。
別の実験結果も見てみましょう。

【実験2】同じ平均値なのに、印象が全然違う
今度は別の日に、別のお客さんで実験しました。
☕ 実験2の結果
| 豆の種類 | 1人目 | 2人目 | 3人目 | 4人目 | 5人目 | 平均 |
|---|---|---|---|---|---|---|
| 豆A | 2 | 10 | 3 | 9 | 6 | 6.0 |
| 豆B | 3 | 10 | 5 | 9 | 8 | 7.0 |
| 豆C | 4 | 10 | 6 | 10 | 10 | 8.0 |
あれ?平均値は実験1と全く同じ(6.0、7.0、8.0)ですね。
でも、データをよく見てください。
実験2は評価のバラつきが大きいのがわかりますか?
- 実験1:各豆の評価が「6〜9点」の狭い範囲に収まっている
- 実験2:各豆の評価が「2〜10点」と大きくバラついている
【核心】どちらの「豆Cが一番」を信じるべき?
ここで重要な問いが生まれます。
🤔 どちらの実験結果を信じるべき?
実験1:バラつきが小さい → 豆Cが本当に良い可能性が高い
実験2:バラつきが大きい → 豆Cが良かったのはたまたまかもしれない
そうなんです。
平均値が同じでも、「信頼度」が全然違うのです。
実験2のように「評価が人によってバラバラ」だと、
たまたま豆Cを評価した人が甘い点をつけた可能性があります。
逆に実験1のように「みんな似たような評価」だと、
豆Cが本当に良いと言える可能性が高くなります。
平均値の差だけを見ても、それが「本当の差」なのか「偶然のバラつき」なのかわからない。
だから、「バラつき(分散)」を分析して、平均の差が信頼できるか判定する必要がある。
これが分散分析(ANOVA)の考え方です!

分散分析の「2つのバラつき」を理解しよう
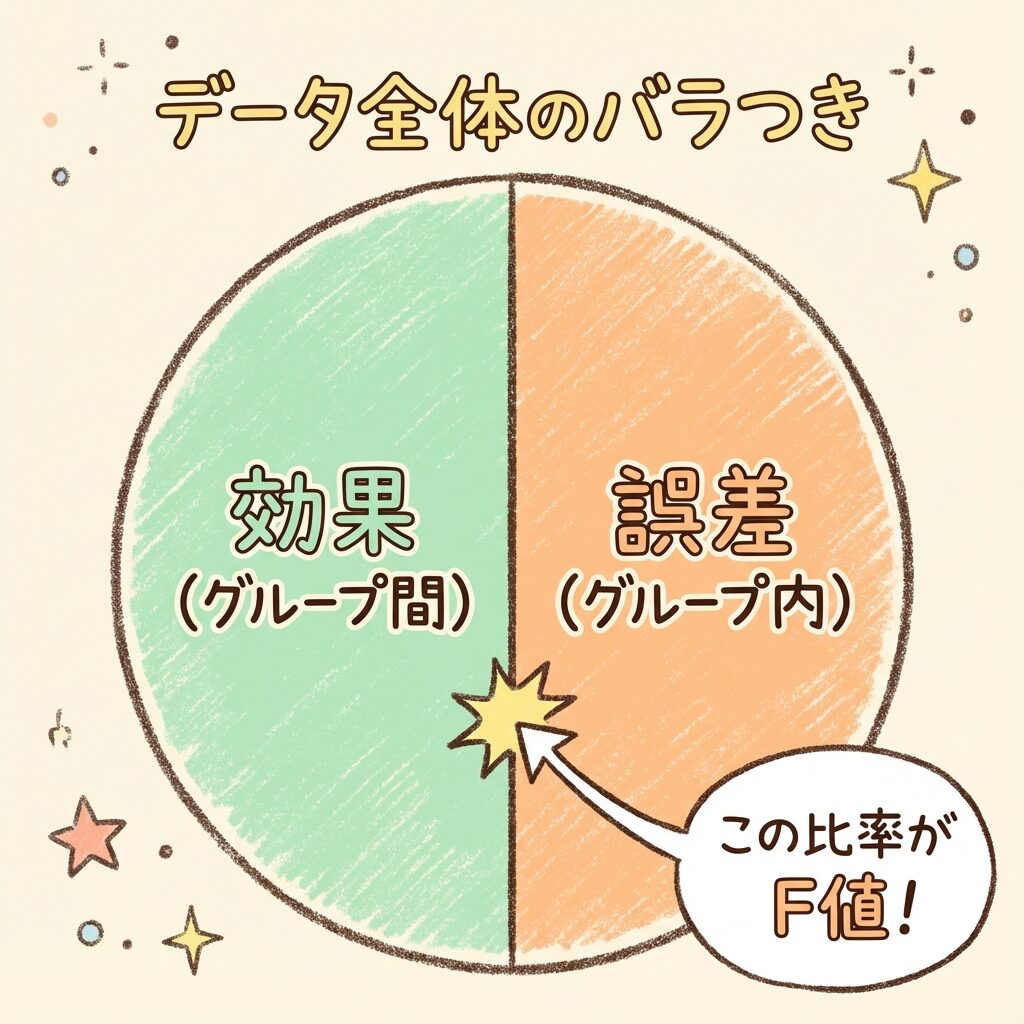
分散分析では、データ全体のバラつきを2つに分解します。
バラつきその①:グループ間のバラつき(効果)
これは、「豆A、豆B、豆Cの平均値がどれだけ離れているか」を表します。
つまり、「コーヒー豆の種類によって、味の評価が変わるか?」という「効果」の大きさです。
✅ グループ間のバラつきが大きい = 効果がある!
豆A、豆B、豆Cの平均点が大きく離れていれば、
「コーヒー豆の種類によって味が変わる」と言えます。
バラつきその②:グループ内のバラつき(誤差)
これは、「同じ豆を飲んでも、人によって評価がバラつく」ことを表します。
味覚は人それぞれ。同じ豆Aを飲んでも、6点をつける人もいれば8点をつける人もいます。
これは「誤差」です。
⚠️ グループ内のバラつきが大きい = 誤差が大きい
同じ豆なのに評価がバラバラだと、
「平均値の差が偶然かもしれない」という不安が増えます。
【図解】2つのバラつきのイメージ
言葉だけではわかりにくいので、図で見てみましょう。
🎯 分散分析のイメージ図
|
【ケース1】効果が大きい場合 🔴🔴🔴 | 🔵🔵🔵 | 🟢🟢🟢
グループがハッキリ分かれている |
【ケース2】誤差が大きい場合 🔴🔵🟢🔴🔵🟢🔴🔵🟢
グループがゴチャ混ぜ |
分散分析の判定方法:F値という「ものさし」
では、分散分析では具体的にどうやって「効果があるか」を判定するのでしょうか?
答えは、「2つのバラつきの比率」を計算することです。
F値 = 効果のバラつき ÷ 誤差のバラつき
F = グループ間の分散(効果)÷ グループ内の分散(誤差)
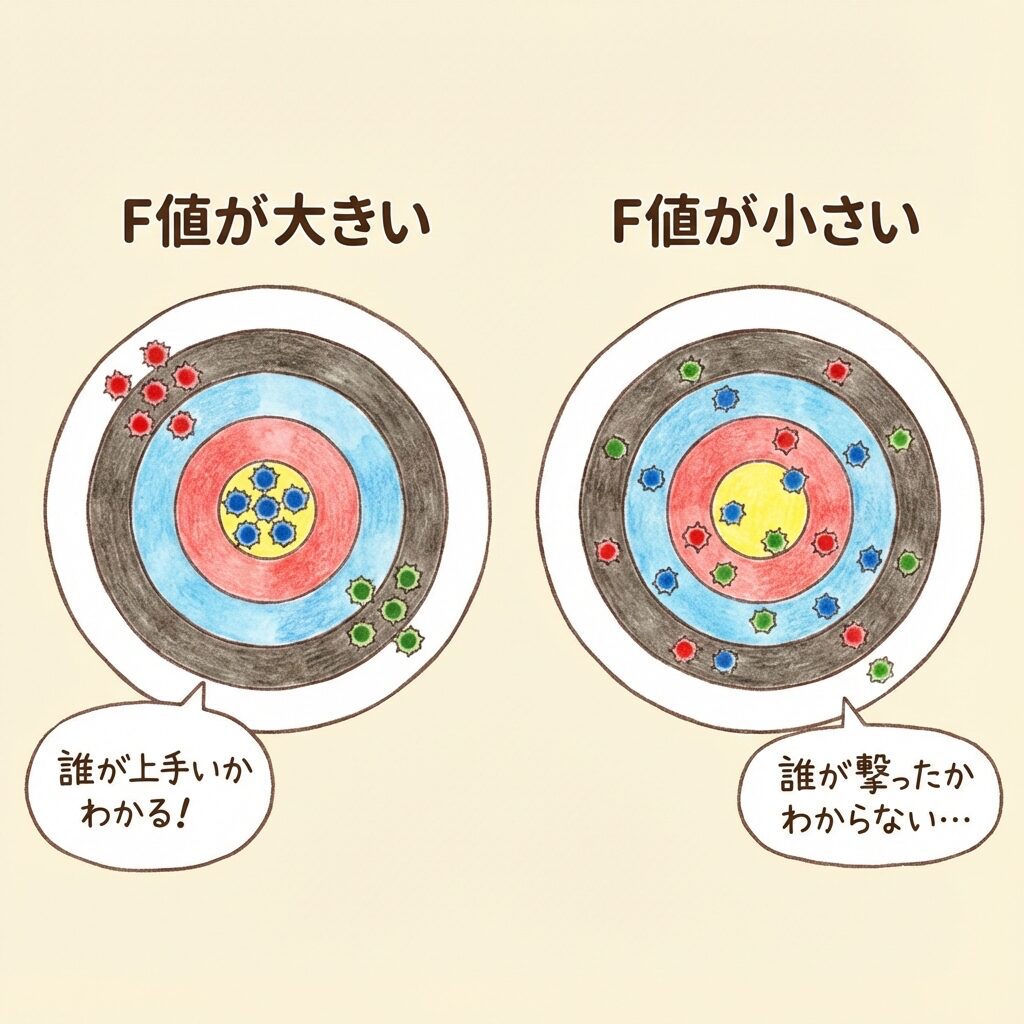
このF値が大きければ大きいほど、「効果がある」と言えます。
F値の解釈:シンプルに考えよう
| F値 | 意味 | 結論 |
|---|---|---|
| F値が大きい | 効果 > 誤差 (平均の差が誤差より大きい) |
効果あり!✅ |
| F値が小さい | 効果 ≦ 誤差 (平均の差が誤差に埋もれている) |
効果なし…❌ |
【たとえ話】会議室での議論
F値をイメージしやすくするために、こんなたとえ話を考えてみましょう。
🏢 会議室のたとえ
あなたは会議室にいます。
3つのチーム(A、B、C)が議論しています。
【ケース1:F値が大きい】
各チームは静かに話し合っている(誤差が小さい)。
でも、チームAとチームCの意見は大きく違う(効果が大きい)。
→ 「チームによって意見が違う」と明確にわかる!
【ケース2:F値が小さい】
各チームの中でも意見がバラバラでガヤガヤ(誤差が大きい)。
チーム間の違いより、チーム内のバラつきの方が目立つ。
→ 「チームによる違い」が騒音に埋もれて聞こえない…
分散分析の全体像:3ステップで理解する
ここまでの内容を整理すると、分散分析は以下の3ステップで行います。
📊 分散分析の3ステップ
Step 1:データ全体のバラつきを計算する
全データの「総平方和」を求める
Step 2:バラつきを「効果」と「誤差」に分解する
グループ間平方和(効果)と グループ内平方和(誤差)に分ける
Step 3:F値を計算して判定する
F値 = 効果の分散 ÷ 誤差の分散 → F分布表と比較して判定
【実験計画法】分散分析表の作り方完全ガイド →
🏭 分散分析が使われる場面
「分散分析って、どこで使うの?」と思うかもしれません。実は、あなたの身近なところでたくさん使われています。
共通しているのは、「複数の選択肢から、どれがベストか決めたい」という場面です。
具体的な活用例
| 分野 | 具体例 |
|---|---|
| 🏭 製造業 | 3種類の原料のうち、どれが最も品質が高いか? |
| 💊 医療 | 3種類の薬のうち、どれが最も効果があるか? |
| 🌾 農業 | 3種類の肥料のうち、どれが最も収穫量が多いか? |
| 📈 マーケティング | 3種類の広告のうち、どれが最もクリック率が高いか? |
| 🎓 教育 | 3種類の教え方のうち、どれが最もテストの点が上がるか? |
すべてに共通しているのは、「複数のグループを比較して、どれが良いか決める」こと。そして、その判断が「偶然ではなく、本当の差だ」と言えるかどうかを、分散分析で確かめるのです。
📝 まとめ:分散分析は「バラつきを見て真実を知る」方法
📌 この記事のポイント
| 分散分析とは? | 平均値の差が「本当の差」か「偶然」かを判定する方法 |
| なぜ平均ではダメ? | バラつきが大きいと、平均の差が「たまたま」かもしれないから |
| 2つのバラつきとは? | ①グループ間(効果) ②グループ内(誤差) |
| どうやって判定する? | F値 = 効果の分散 ÷ 誤差の分散 で判定 |
「平均値の差」が「偶然のバラつき」より大きければ、
それは「本当の差」である。
この考え方がわかれば、分散分析の8割は理解したようなものです。あとは、具体的な計算方法を学んでいくだけ。
ぜひ、この記事をスタート地点にして、実験計画法の世界を探検してみてください。データを正しく分析できるようになると、仕事でも研究でも「判断の精度」が格段に上がりますよ。
📖 次に読む記事
一元配置実験シリーズ|次の記事
一元配置実験とは?1つの因子で白黒つける実験の基本形|一元配置実験②
分散分析の考え方がわかったら、次は「一元配置実験」を学びましょう。1つの因子(条件)だけを変えて効果を調べる、最もシンプルな実験方法です。
次の記事を読む →🔗 関連記事
あなたの悩みに合わせて、以下の記事も参考にしてください。
🔰「実験計画法を最初から体系的に学びたい」
📊「誤差って何?バラつきの正体を知りたい」
🧪「因子と水準の違いがわからない」
🎯「実験の3原則(ランダム化・反復・局所管理)を知りたい」
📐「QC検定対策として分散分析を学びたい」
📚 一元配置実験シリーズ|全15回
このシリーズを順番に読めば、一元配置実験を完全マスターできます。
- 分散分析とは?「平均の差」ではなく「分散」を見る理由 ← 今ここ
- 一元配置実験とは?1つの因子で白黒つける実験の基本形
- 修正項(CT)とは?T²/Nの計算式を図解で理解する
- 平方和(S)と自由度の関係|「分散」を求める準備
- 総平方和(S_T)の計算|データ全体のバラつきを数値化する
- 群間平方和と群内平方和|バラつきを「効果」と「誤差」に分解する
- 分散分析表(ANOVA)の作り方|表を完成させる手順
- F検定で有意差を判定する|F分布表の使い方
- 母平均の点推定と区間推定|最適条件の結果を予測する
- 有効繰返し数とは?実験回数の最適解を導く考え方
- 有効繰返し数の計算方法|2つの公式を使い分ける
- 平均平方の期待値E(V)とは?数式の意味を直感的に理解する
- 分散分析表の作り方完全ガイド|S→V→Fの流れを総復習
- 一元配置実験の分散分析を実践|カレーの例で手を動かす
- 一元配置実験の計算を完全図解|分散分析表を1から作る全手順
🎯 最後まで読んでいただき、ありがとうございました。
「分散分析」という言葉に苦手意識を持っていた方も、
「なるほど、そういうことか!」と思っていただけたら嬉しいです。
