- P値が「成功率」ではなく「偶然の確率」だとわかる
- 有意水準αが「自分で決める基準」だと理解できる
- 「P < 0.05 で有意」の本当の意味がスッキリわかる
- 検定の判定ロジックをイメージで理解できる
統計的検定の結果を見るとき、必ず登場するのがこの2つです。
(P-value)
(Significance Level)
「P値が0.05より小さければOK」
手順としてそう覚えている人は多いですが…
「そもそもこの0.05って何?」
「Pって何の確率?」
と聞かれると、答えに詰まってしまうことが多いものです。
実はこの検定のプロセス、私たちが日常的に行っている「疑い深さ」の心理メカニズムそのものなんです。
今日は、難しい数式の代わりに「イカサマコイン」の例えを使って、この2つの正体を直感的に理解しましょう。
目次
背理法:あえて「偶然だ」と言い張ってみる
P値を理解するために、まず検定の基本ロジックを復習しましょう。
検定は、数学の証明方法である「背理法(はいりほう)」を使っています。
「とりあえず相手の主張(偶然である)を認めておいて、
そこから矛盾を突きつける」という論法です。
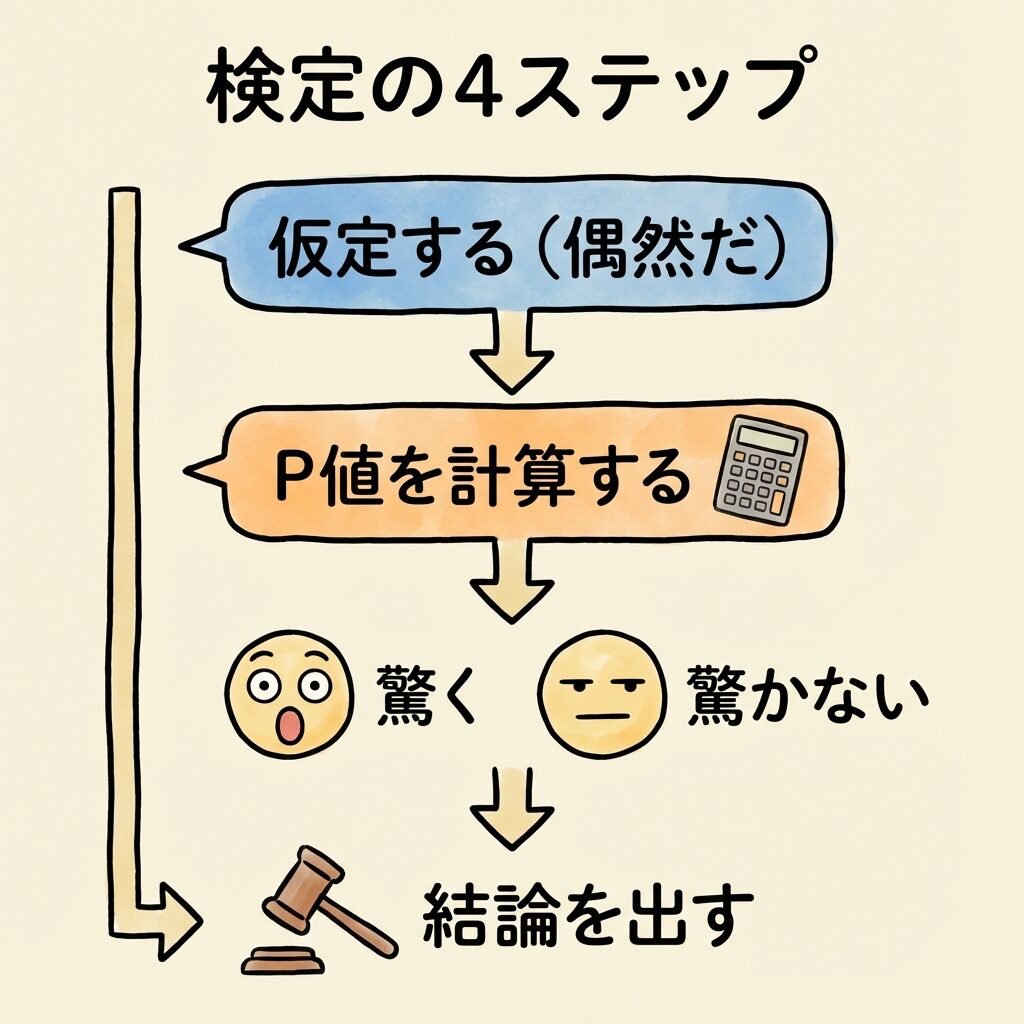
検定の思考プロセス(4ステップ)
「何も特別なことは起きていない(偶然だ)」と仮定する
→ これが「帰無仮説」
その仮定のもとで、今回のデータが得られる確率を計算する
→ これが「P値」
「うわっ、こんなレアな結果が!」or「まあ、普通だね」
レアすぎるなら「偶然じゃない!」と結論づける
→ これが「帰無仮説を棄却」
この中で、ステップ2の「P値」とステップ3の「どこからがレア?」という基準(有意水準α)が、今回のテーマです。
P値とは「驚きのスコア」である
P値の「P」は Probability(確率) の頭文字です。
でも、実務上は「驚きのスコア」と読み替えると分かりやすくなります。
| P値が大きい (0.5など) |
よくあること。 「ふーん、普通だね」😐 |
| P値が小さい (0.01など) |
めったにないこと。 「えっ!? マジで?」😲 |
例え話:友人のコイン投げ
友人が「このコイン、表が出やすいイカサマコインなんだぜ」と言って、目の前で5回投げました。
結果は、5回連続で「表」でした。
さて、これは偶然でしょうか?
普通のコインで5回連続表が出る確率は…
この 「0.03」こそがP値 です!
「普通のコインだとしたら、こんなこと3%の確率でしか起きないよ。
そんなレアなことが、今いきなり目の前で起きたの?」
この「レア度(0.03)」を突きつけられると、私たちは…
「うーん、それは偶然とは考えにくいな。やっぱりイカサマ(差がある)なんじゃないか?」
と疑い始めますよね。

有意水準(α)とは「疑うためのライン」
では、P値がいくら以下なら「偶然じゃない(イカサマだ)」と断定していいのでしょうか?
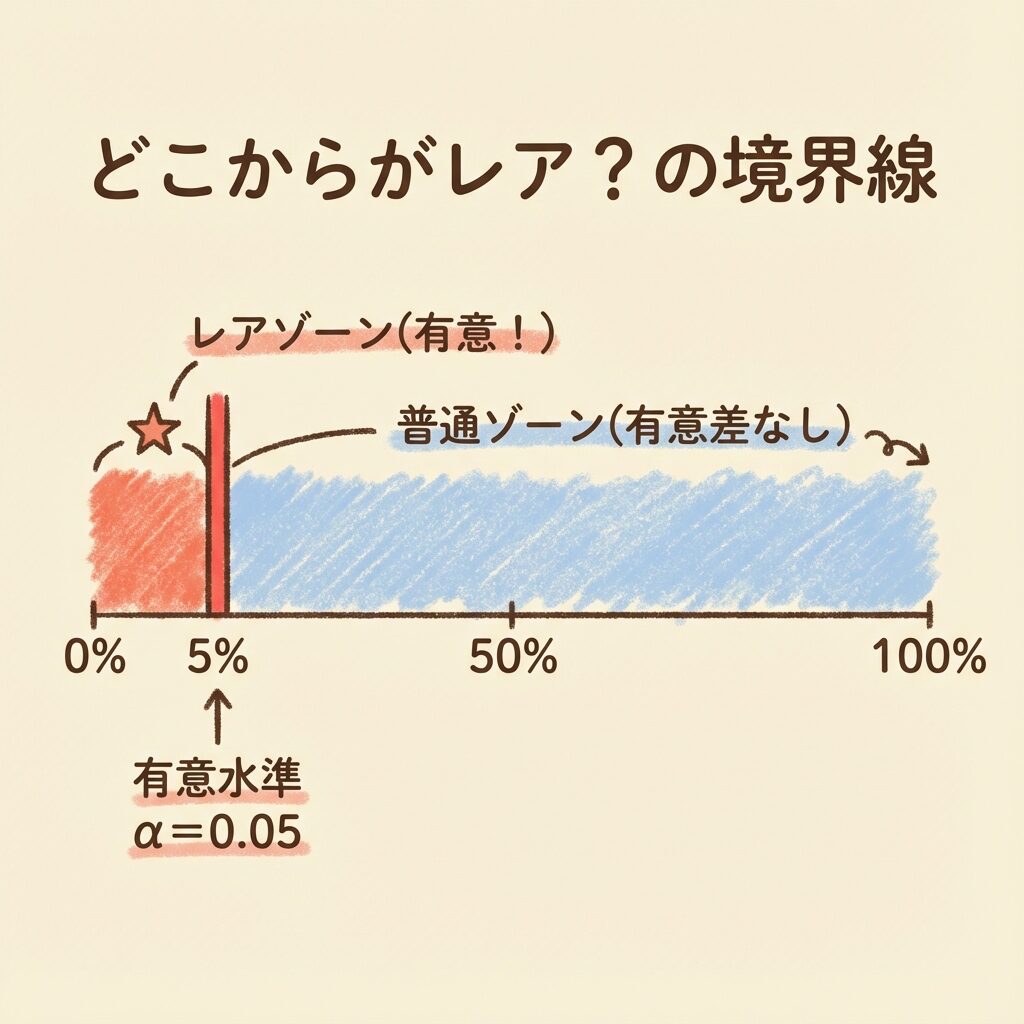
どこからが「レア」?という問題
確率3%なら疑いますが…
もし3回連続(確率12.5%)だったらどうでしょう?
と許してしまうかもしれません。
この「ここまでは偶然として許すけど、これよりレアなら許さない(疑う)」という境界線のことを、有意水準(α)と呼びます。
「この確率より低いことが起きたら、偶然ではないとみなす!」
というあなたが決める基準です。
よく使われる有意水準
| 有意水準 | 意味 | 使われる場面 |
|---|---|---|
| α = 0.05 (5%) |
「20回に1回以下のレアなこと」が起きたら疑う | 工場の品質管理 一般的な研究 (最も一般的) |
| α = 0.01 (1%) |
「100回に1回以下の奇跡」が起きない限り認めない | 命に関わる医療 絶対に間違えられない検査 (厳しい基準) |
有意水準 α は、計算して出すものではありません。
実験をする人間(あなた)が「最初に決める」決意です。
「5%より珍しいことが起きたら、偶然とは認めないぞ!」という宣言です。
判定:「5%の奇跡」は信じない
検定の最後に行うのは、「P値」と「有意水準 α」の背比べです。
判定ルールはシンプル!
(例:0.03 < 0.05)
「偶然だとしたら3%しか起きない現象が起きた。
私が決めた基準(5%)よりもレアだ」
(帰無仮説を棄却)
(例:0.12 > 0.05)
「偶然だとしたら12%で起きる現象だ。
まあ、基準(5%)よりはよくあることだ」
(帰無仮説を棄却できない)
「5%以下の奇跡が起きたら、
それは奇跡ではなく、何らかの仕掛け(必然)があるはずだ」
と考える。これが統計的検定の正体です。

具体例で判定してみよう
先ほどのコイン投げの例で、実際に判定してみましょう。
ケース:5回連続で表が出た
| P値(計算結果): | 0.03(3%) |
| 有意水準α(自分で設定): | 0.05(5%) |
| 比較: | 0.03 < 0.05 ✓ |
P値(0.03)< 有意水準(0.05)なので…
有意差あり!(イカサマだ!)
「普通のコインで5回連続表が出る確率は3%。
5%より低いから、偶然とは考えにくい。
このコインはイカサマ(表が出やすい)と判断する!」
よくある勘違いを正す
最後に、P値についてよくある勘違いを正しておきましょう。
P値は「成功率」ではない!
「P値 = 0.03 だから、
この新薬は97%の確率で成功する!」
「何の効果もない偽薬だとしても、
3%の確率でたまたまこれくらい効いちゃうことがあるよ」
P値はあくまで「帰無仮説が正しいとした場合に、このデータが得られる確率」です。
小さければ小さいほど、
「偶然なわけあるか!」と強くツッコミを入れられる
(=結果に自信が持てる)、と覚えておけば間違いありません。
まとめ|P値と有意水準αの関係
「帰無仮説が正しいとした場合に、このデータが得られる確率」
→ 小さいほど「レア」で「偶然とは思えない」
「どこからをレアとみなすか」という自分で決める基準
→ 一般的には5%(0.05)が使われる
P値 < α なら「有意差あり」(帰無仮説を棄却)
P値 ≥ α なら「有意差なし」(帰無仮説を棄却できない)
次に学ぶべきこと
P値と有意水準の関係がわかったところで、一つ疑問が出てきませんか?
「有意水準を厳しくすれば(1%にすれば)、
間違いが減って良いのでは?」
実は、有意水準を厳しくしすぎると別の問題が発生します。
それが「第1種の過誤」と「第2種の過誤」のトレードオフです。
次の記事では、この2つの「間違いのタイプ」を、「あわてんぼう」と「ぼんやり者」の例えでスッキリ解説します。
💪 ここまで読んでくださった方へ
「P値が0.05より小さければOK」
この呪文のような言葉の意味、もうバッチリですね!
「5%の奇跡が起きたら、それは奇跡じゃない」
このイメージを持っていれば、
検定結果の解釈で迷うことはなくなります。
次は「間違いの種類」を学んで、
検定マスターへさらに近づきましょう!
