- Z検定がどんな検定かイメージでわかる
- なぜ「実務では使わない」のに学ぶ必要があるのか理解できる
- 1.96という「魔法の数字」の意味がわかる
- Z検定とt検定の違いがスッキリ理解できる
統計学を勉強していると、必ず最初に出てくるのが「Z検定」です。
でも、教科書を読んでこんな疑問を持ちませんでしたか?
🤔 「母分散が既知のとき」って、そんな状況ある?
🤔 実際に使うのはt検定って聞いたけど、なんでZ検定を学ぶの?
🤔 1.96ってどこから出てきた数字なの?
結論から言うと、Z検定は「神様の視点」を持った理想的な検定です。
実務では使わないのに学ぶ理由は、t検定を理解するための「土台」だからです。
今回は、Z検定を「神様と人間」のたとえで、イメージで理解していきましょう。
目次
Z検定とは?|「真の分散を知っている」という贅沢な状況
Z検定を理解するために、まず「母分散」について確認しましょう。
「母分散」とは何か?
分散とは、データの「バラつき具合」を数値化したものでしたね。
そして「母分散(σ²)」とは、母集団全体の「真のバラつき」のことです。
ある工場で作る部品の長さが「平均50mm、標準偏差5mm」だとします。
この「標準偏差5mm(分散25)」が母分散です。
でも現実には、この「5mm」を正確に知っている人はいません。
神様だけが知っている「真の値」なのです。
「神様」と「人間」の違い
Z検定とt検定の違いを「神様と人間」でたとえてみましょう。

| 神様の視点 (Z検定) |
人間の視点 (t検定) |
|
|---|---|---|
| 母分散σ² | 既知 (神様だけが知っている) |
未知 (普通は知らない) |
| 使う分布 | 正規分布(Z分布) | t分布 |
| 判定基準 (α=5%) |
1.96 (固定値) |
自由度で変わる (表を見る) |
| 実務での使用頻度 | ほぼゼロ (理論上の話) |
非常に多い (実務の主役) |
つまり、Z検定は「もし神様みたいに母分散を知っていたら」という理想的な状況での検定なのです。
なぜ「使わない検定」を学ぶのか?
「実務で使わないなら、なんで勉強するの?」と思いますよね。
理由は2つあります。
① t検定を理解するための「土台」になる
Z検定の公式を理解していれば、t検定は「分散を推定するバージョン」として理解できます。
② 「1.96」という魔法の数字の意味がわかる
統計学で頻出する「1.96」は、Z検定から来ています。この数字の意味を知ると、信頼区間の計算もスッキリ理解できます。
「1.96」の正体|95%信頼区間の魔法の数字
統計学を勉強していると、何度も「1.96」という数字に出会いますよね。
この数字は、正規分布の「両側5%点」から来ています。
正規分布の「95%の範囲」
正規分布(ベルカーブ)を思い出してください。
平均を中心に、左右に「±1.96σ」の範囲を取ると、全体の95%が収まります。
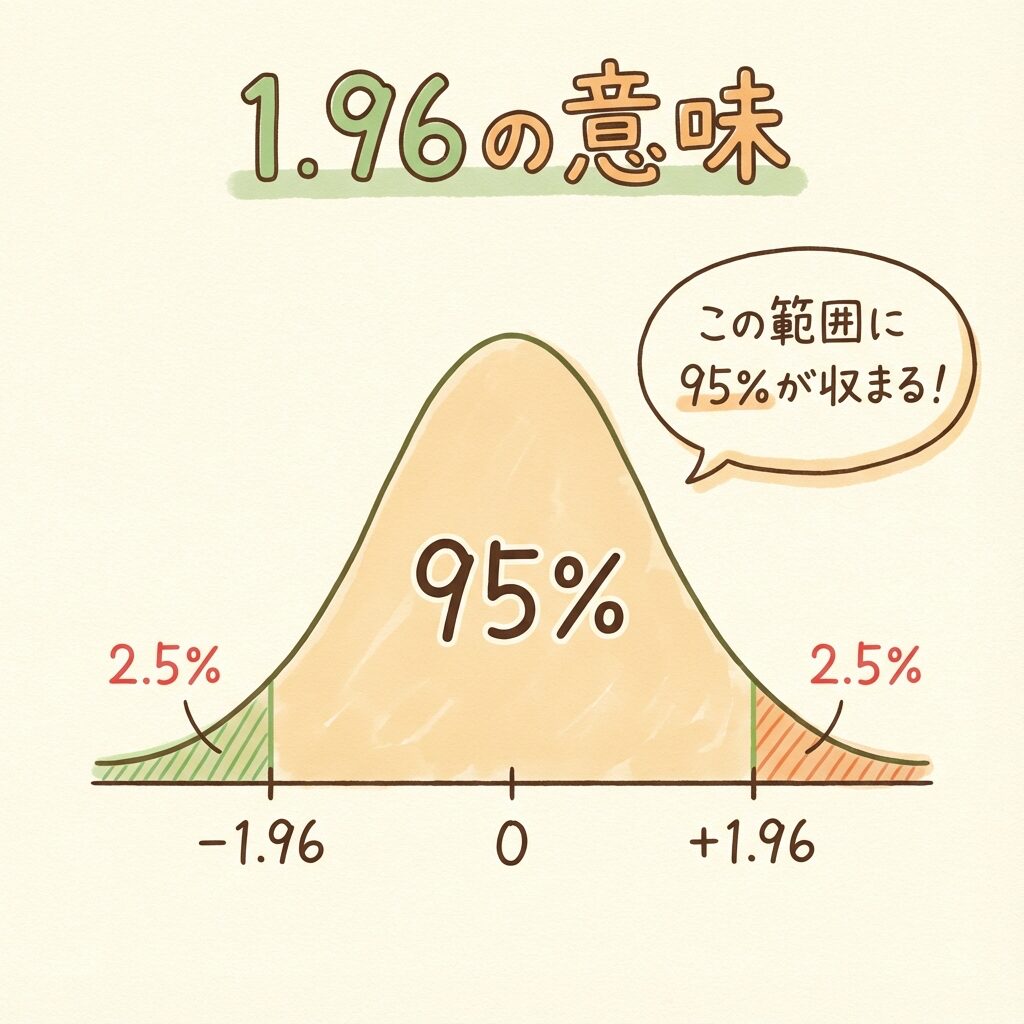
📊 正規分布の「95%の範囲」
← 2.5% ← | ← 95% → | → 2.5% →
-1.96 ───────── 0 ───────── +1.96
平均から±1.96σの範囲に、データの95%が収まる
逆に言うと、「5%しか起こらないこと」が起きたら、それは偶然ではなく何か原因があると疑うのが、有意水準5%での検定です。
Z値の意味
Z検定では、データを「Z値」に変換します。
Z = (標本平均 − 母平均) / (母標準偏差 / √n)
この公式の意味を、日本語で説明すると…
💡 Z値の意味
「サンプルの平均値が、母平均からどれくらい離れているか」を、
「標準誤差」という単位で測った数値です。
例:Z=2.5 なら「母平均から標準誤差2.5個分離れている」
このZ値が「±1.96」を超えたら、「5%しか起こらないことが起きた!」と判断し、帰無仮説を棄却します。
具体例で計算してみよう
実際に計算してみましょう。「神様の視点」を持っている架空の例です。
例題:ボルトの長さは規格通り?
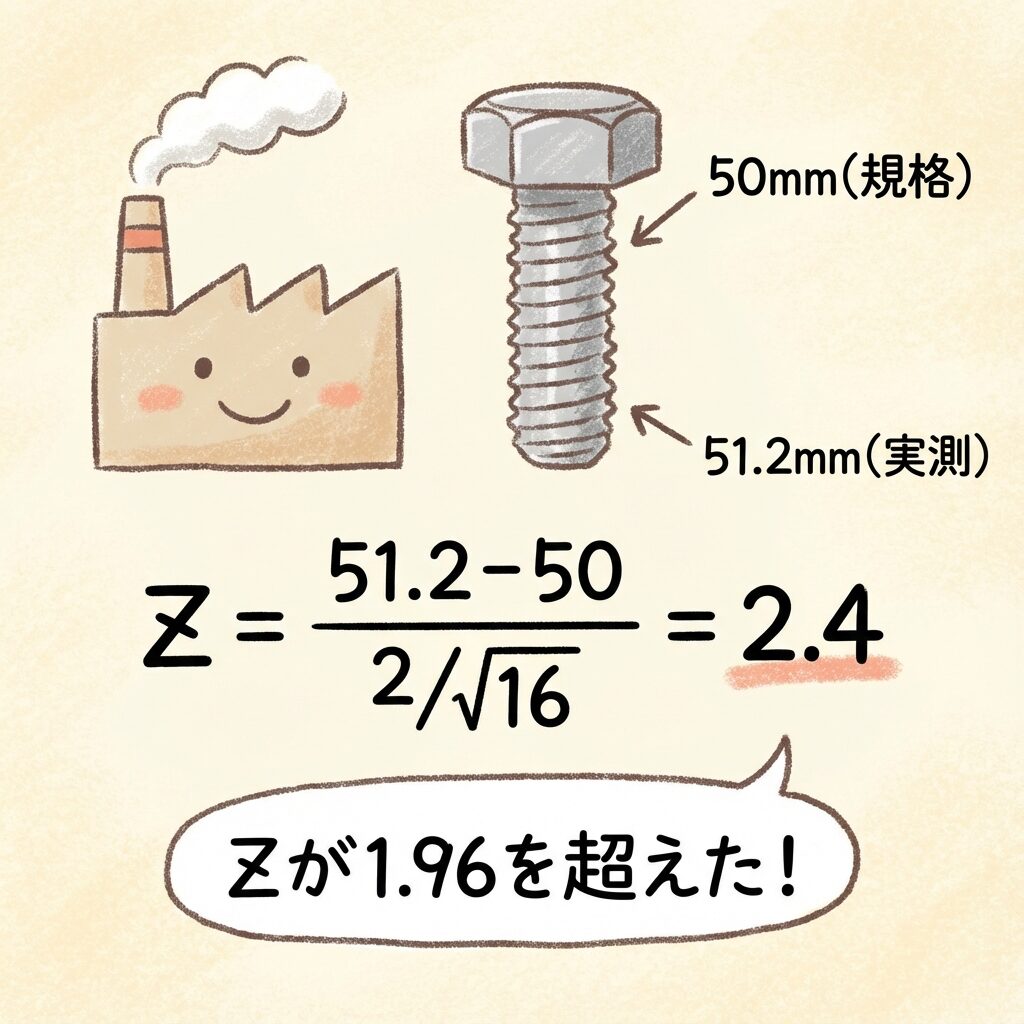
📋 問題設定
- ある工場のボルトは、平均50mmで作られている(規格値)
- 母標準偏差σ = 2mmであることが、長年の蓄積データから判明している(神様の知識)
- 今日の生産ラインからn=16本をサンプリングしたら、平均51.2mmだった
- この51.2mmは、「たまたまのブレ」か「異常」か?
Step 1:仮説を立てる
帰無仮説 H₀:母平均 μ = 50mm(規格通り)
対立仮説 H₁:母平均 μ ≠ 50mm(規格から外れている)
Step 2:Z値を計算する
Z = (51.2 − 50) / (2 / √16)
Z = 1.2 / 0.5
Z = 2.4
Step 3:判定する
有意水準α=5%(両側検定)の場合、判定基準は±1.96です。
棄却域(左側)
Z < -1.96
採択域
-1.96 ≤ Z ≤ 1.96
棄却域(右側)
Z > 1.96
計算結果はZ = 2.4です。これは1.96を超えているので…
🚨 判定結果
帰無仮説を棄却する
→ ボルトの長さは規格から外れていると判断できる
Z検定の限界|「神様の知識」がないとき
さて、ここまでZ検定を見てきましたが、大きな問題があります。
「母標準偏差σ = 2mm」
この値、どうやって知ったの?
現実には、「長年の蓄積データがある」なんて状況はほぼありません。
普通は母分散(真のバラつき)は未知です。
だからこそ、実務では「母分散がわからなくても使える検定」が必要です。
それがt検定です。
t検定では、母分散の代わりに「サンプルから計算した分散」を使います。
でも、サンプルの分散は「推定値」なので、ちょっと不確実。
その不確実さを反映するために、正規分布ではなく「t分布」という、裾野が広がった分布を使うのです。

まとめ|Z検定は「理想世界の検定」
📝 この記事のまとめ
- Z検定は、母分散(真のバラつき)が既知のときに使う検定
- 現実には母分散を知っていることはほぼないので、「神様の検定」とも言える
- 1.96は正規分布の「両側5%点」で、α=5%の判定基準
- 実務ではZ検定は使わず、t検定を使う
- でも、Z検定を理解しているとt検定の理解が深まる
🎓 覚え方のコツ
Z検定 = 「神様の検定」
真のσを知っている理想的な状況での検定
次に読むべき記事
Z検定の考え方を理解したら、次は実務で使う「t検定」を学びましょう。
t検定では、「神様の知識(母分散)」がなくても検定ができます。
その代わり、判定基準が「1.96」ではなく、自由度によって変わるようになります。
【計算例あり】t検定(一標本)|「規格通りか?」を検証する実務の基本 →
📚 関連記事
💪 ここまで読んでくださった方へ
「Z検定」という「神様の検定」を理解できましたね!
この記事で学んだ「1.96」という数字は、
今後、信頼区間の計算などで何度も登場します。
次は、私たち「人間」が使うt検定を学びましょう!
統計学のおすすめ書籍
統計学の「数式アレルギー」を治してくれた一冊
「Σ(シグマ)や ∫(インテグラル)を見ただけで眠くなる…」 そんな私を救ってくれたのが、小島寛之先生の『完全独習 統計学入門』です。
この本は、難しい記号を一切使いません。 「中学レベルの数学」と「日本語」だけで、検定や推定の本質を驚くほど分かりやすく解説してくれます。
「計算はソフトに任せるけど、統計の『こころ(意味)』だけはちゃんと理解したい」 そう願う学生やエンジニアにとって、これ以上の入門書はありません。
【QC2級】「どこが出るか」がひと目で分かる!最短合格へのバイブル
私がQC検定2級に合格した際、使い倒したのがこの一冊です。
この本の最大の特徴は、「各単元の平均配点(何点分出るか)」が明記されていること。 「ここは出るから集中」「ここは出ないから流す」という戦略が立てやすく、最短ルートで合格ラインを突破できます。
解説が分かりやすいため、私はさらに上の「QC1級」を受験する際にも、基礎の確認用として辞書代わりに使っていました。 迷ったらまずはこれを選んでおけば間違いありません。


