目次
💡 こんな疑問、ありませんか?
「主成分分析って、結局何をやってるの?」
「Z₁ = a₁₁x₁ + ... って式が出てきたけど、なぜこの式なのかがわからない…」
「第1主成分が『最大分散』って、どういう意味?」
✅ この記事では、中学生でも理解できるレベルで「主成分の導出」を徹底解説します。
✅ QC検定1級合格に必要な範囲に絞り、イメージ重視で「なぜそうなるのか?」を丁寧に説明します。
静かに充実した生活を送る
目次
「主成分分析って、結局何をやってるの?」
「Z₁ = a₁₁x₁ + ... って式が出てきたけど、なぜこの式なのかがわからない…」
「第1主成分が『最大分散』って、どういう意味?」
✅ この記事では、中学生でも理解できるレベルで「主成分の導出」を徹底解説します。
✅ QC検定1級合格に必要な範囲に絞り、イメージ重視で「なぜそうなるのか?」を丁寧に説明します。
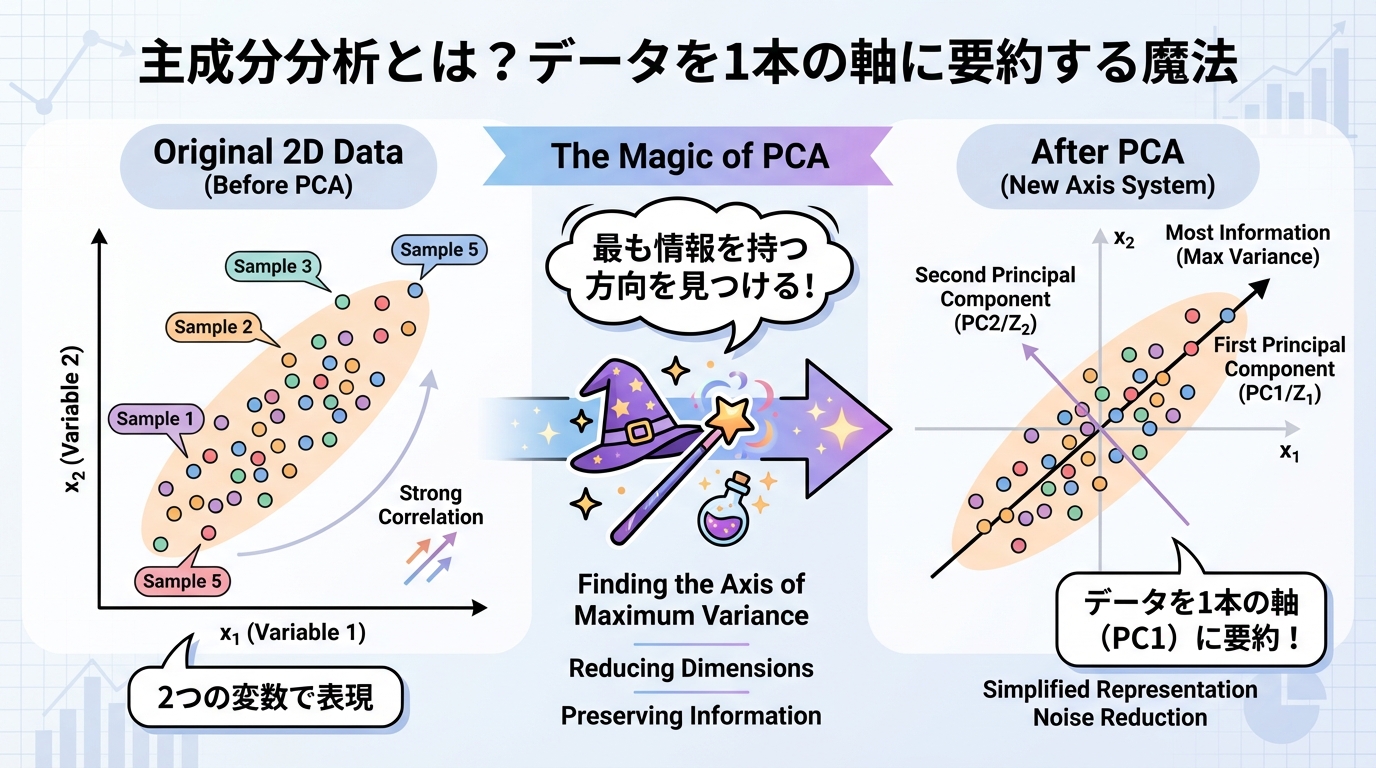
主成分分析(Principal Component Analysis, PCA)は、「たくさんの変数(次元)を、なるべく情報を失わずに少ない変数にまとめる」手法です。
3次元の立体を、2次元の平面に投影すると「影」ができますよね?
この時、どの角度から光を当てるかで、影の形(情報量)が変わります。
主成分分析は、「一番情報が残る角度(方向)」を数学的に見つける方法なんです! 🎯
Z₁ = a₁₁x₁ + a₁₂x₂ + ... + a₁ₚxₚ
この式の意味を、順を追って説明します。
つまり、元の変数を組み合わせて新しい指標(Z₁)を作るということです! 📊
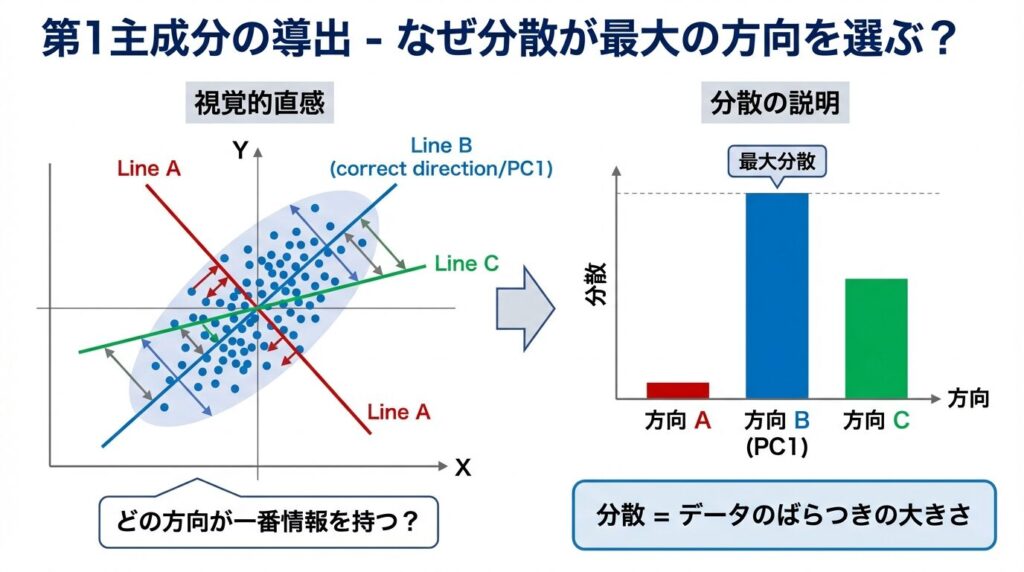
ここが主成分分析の最大のポイントです。
💡 分散が大きい= データがその方向に大きくばらついている
= その方向に多くの情報が詰まっている! 📈
例えば、数学と理科のテストのデータがあったとします。
だから、「分散が最大になる方向」を第1主成分として選ぶんです! 🎯
条件1: Z₁の分散を最大化する
条件2: 係数の二乗和 = 1 (a₁₁² + a₁₂² + ... + a₁ₚ² = 1)
→ これは「単位ベクトル」という制約(長さを1に固定)
この制約がないと、係数を無限に大きくすれば分散も無限に大きくなってしまうため、「方向」だけを決めるために長さを1に固定します。
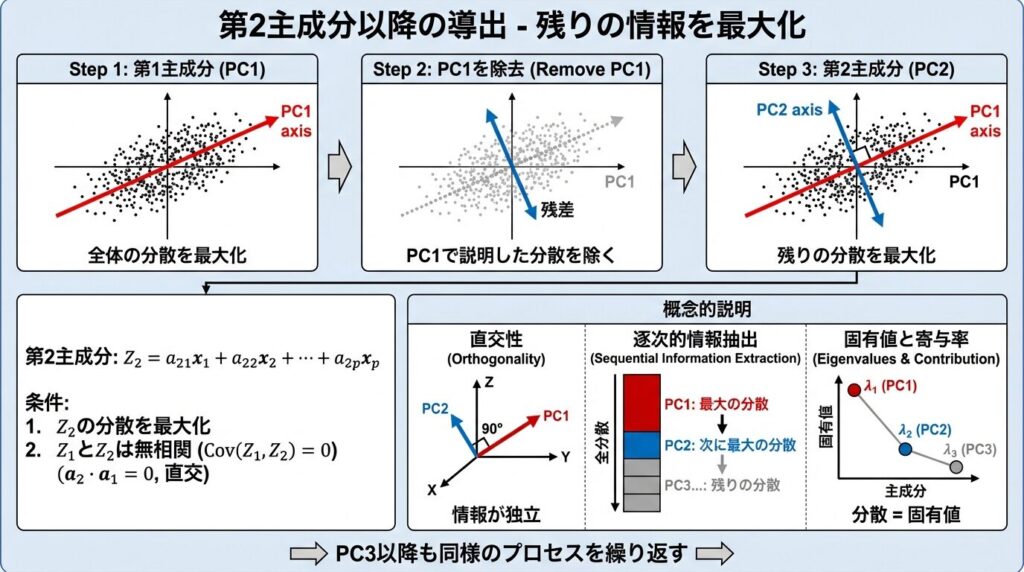
Z₂ = a₂₁x₁ + a₂₂x₂ + ... + a₂ₚxₚ
第2主成分は、第1主成分で説明できなかった「残りの情報」の中で、最も分散が大きい方向を選びます。
第2主成分は、第1主成分と直交(90度の角度)する方向に設定します。
💡 直交する= 相関係数がゼロ = 「独立した別の視点」ということです!
条件1: Z₂の分散を最大化する(ただし第1主成分以外で)
条件2: Z₁とZ₂は無相関(Cov(Z₁, Z₂) = 0)
条件3: 係数の二乗和 = 1 (a₂₁² + a₂₂² + ... + a₂ₚ² = 1)
この条件を満たす方向を選ぶことで、第1主成分の次に重要な情報を抽出できます。
数学、国語、理科、社会の4科目の成績データがあるとします。
Z₁とZ₂は直交しているので、独立した2つの視点で学生を評価できます! 🎓
第3主成分(Z₃)、第4主成分(Z₄)…も、同じルールで導出されます。
こうして、元の変数の数(p個)と同じ数だけ主成分を作ることができます。
💡 ポイント:通常は、上位2〜3個の主成分だけで全体の8〜9割の情報を説明できます!
だから「次元削減」として使えるんです! 🎯
QC検定1級では、計算の流れと解釈が問われます。実際の手順を見ていきましょう。
各変数のスケール(単位)が異なる場合、標準化(平均0、標準偏差1)します。
標準化: z = (x - μ) / σ
例:身長(cm)と体重(kg)は単位が違うので、標準化してから分析します。
共分散行列(または相関行列)の固有値・固有ベクトルを求めます。
例:
固有値: λ₁ = 2.1, λ₂ = 0.7, λ₃ = 0.2
固有ベクトル(PC1): a₁₁ = 0.58, a₁₂ = 0.58, a₁₃ = 0.57
→ 第1主成分: Z₁ = 0.58x₁ + 0.58x₂ + 0.57x₃
(1) 寄与率(Contribution Rate)
寄与率 = λᵢ / Σλ × 100(%)
例:
→ 上位2主成分で93%の情報を説明できる! 🎯
(2) 主成分負荷量(Loading)
各変数と主成分の相関係数。どの変数が主成分に強く影響しているかを示します。
(3) 主成分得点(Score)
各サンプルの主成分上の位置。散布図(スコアプロット)で可視化すると、データの特徴が見えます。
製品の品質特性(寸法A、寸法B、重量、硬度、…10項目)があるとします。
→ 10項目を2つの指標に圧縮して管理できる! 効率的! ✨
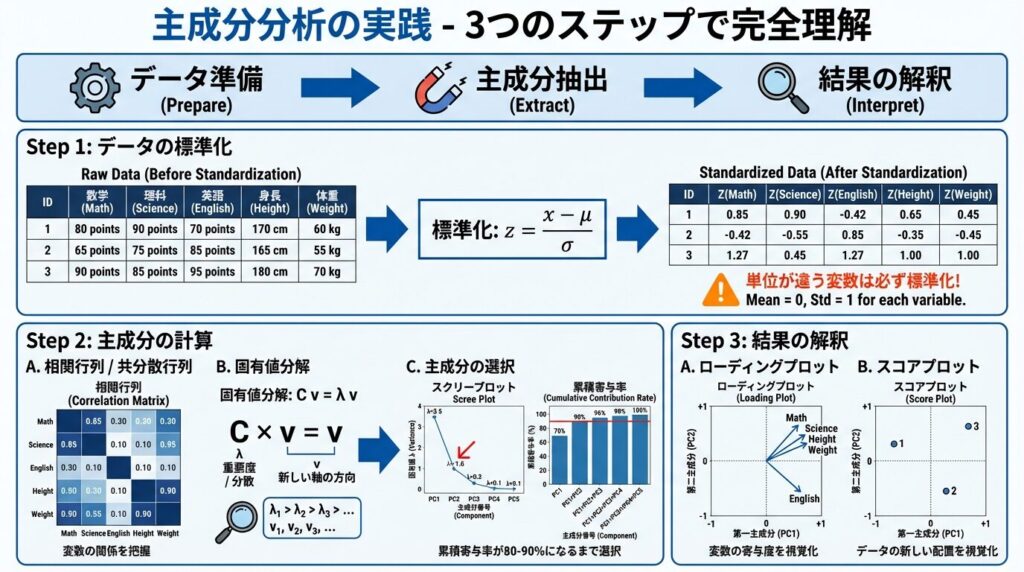
QC検定1級では、計算手順と結果の解釈(寄与率、スコアプロット)が頻出です! 📝
🎉 この記事が役に立ったら、SNSでシェアしてくださいね!
一緒にQC検定1級合格を目指しましょう! 💪✨