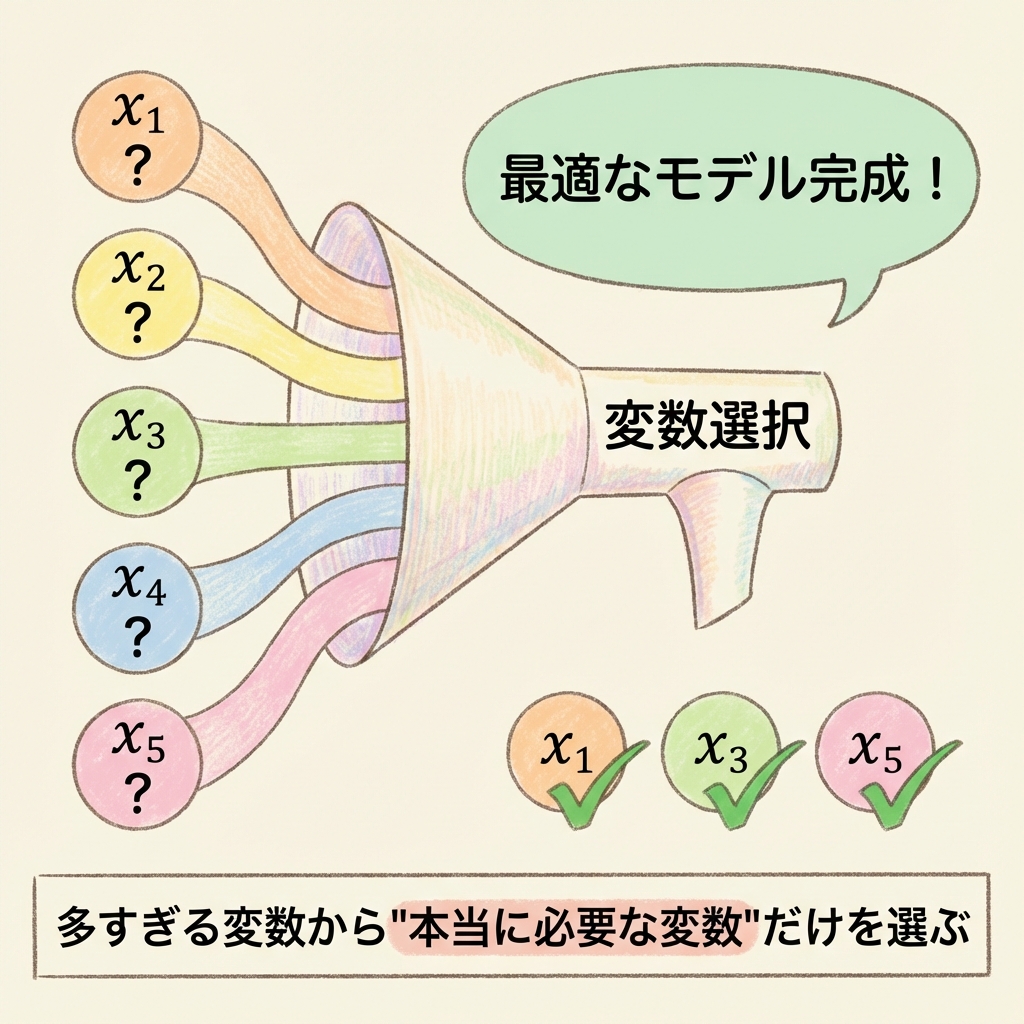
- 説明変数の候補がたくさんあるけど、どれを使えばいいの?
- 全部入れたらダメ?少なすぎてもダメ?
- ステップワイズ法とかAICとか、聞いたことはあるけどよくわからない…
- なぜ「変数選択」が必要なのか
- 増加法・減少法・ステップワイズ法の違いと手順
- AIC(赤池情報量基準)の考え方と使い方
「売上を予測したい。使えそうな変数は10個ある。全部入れればいいの?」
…実は、それはよくない選択です。
変数を入れすぎると、モデルが複雑になりすぎて「過学習」を起こします。逆に、変数が少なすぎると、大事な情報を見逃してしまいます。
じゃあ、どうやって「ちょうどいい変数の数」を決めればいいのでしょうか?
そこで登場するのが「変数選択」の手法です。
この記事では、変数選択の代表的な方法である「増加法」「減少法」「ステップワイズ法」、そしてモデルの良さを測る「AIC」について、図解でわかりやすく解説します。
なぜ「変数選択」が必要なのか?
変数が多すぎる問題|「過学習」のワナ
「変数は多い方が予測精度が上がるんじゃないの?」
直感的にはそう思いますよね。でも、実際は逆です。
変数を増やしすぎると、「過学習(オーバーフィッティング)」という問題が起きます。
過去問を丸暗記した学生がいます。
過去問では100点。でも、本番のテストでは30点…。
これが「過学習」です。
手元のデータ(過去問)には完璧にフィットするけど、
新しいデータ(本番)には全く対応できない状態。
変数を増やすと、手元のデータへの当てはまり(決定係数R²)は必ず上がります。でも、それは「過去問を丸暗記」しているだけかもしれません。
本当に欲しいのは、新しいデータでも予測できるモデルですよね。
変数が少なすぎる問題|「過少適合」のワナ
逆に、変数が少なすぎても問題です。
本当は売上に影響している「広告費」を入れ忘れたら、予測精度はガタ落ちですよね。
これを「過少適合(アンダーフィッティング)」と言います。
| 状態 | 変数の数 | 問題点 |
|---|---|---|
| 過少適合 | 少なすぎる | 重要な情報を見逃す → 予測精度が低い |
| ちょうどいい | 適切 | 必要な情報だけを使う → 予測精度が高い |
| 過学習 | 多すぎる | ノイズまで学習 → 新しいデータで使えない |
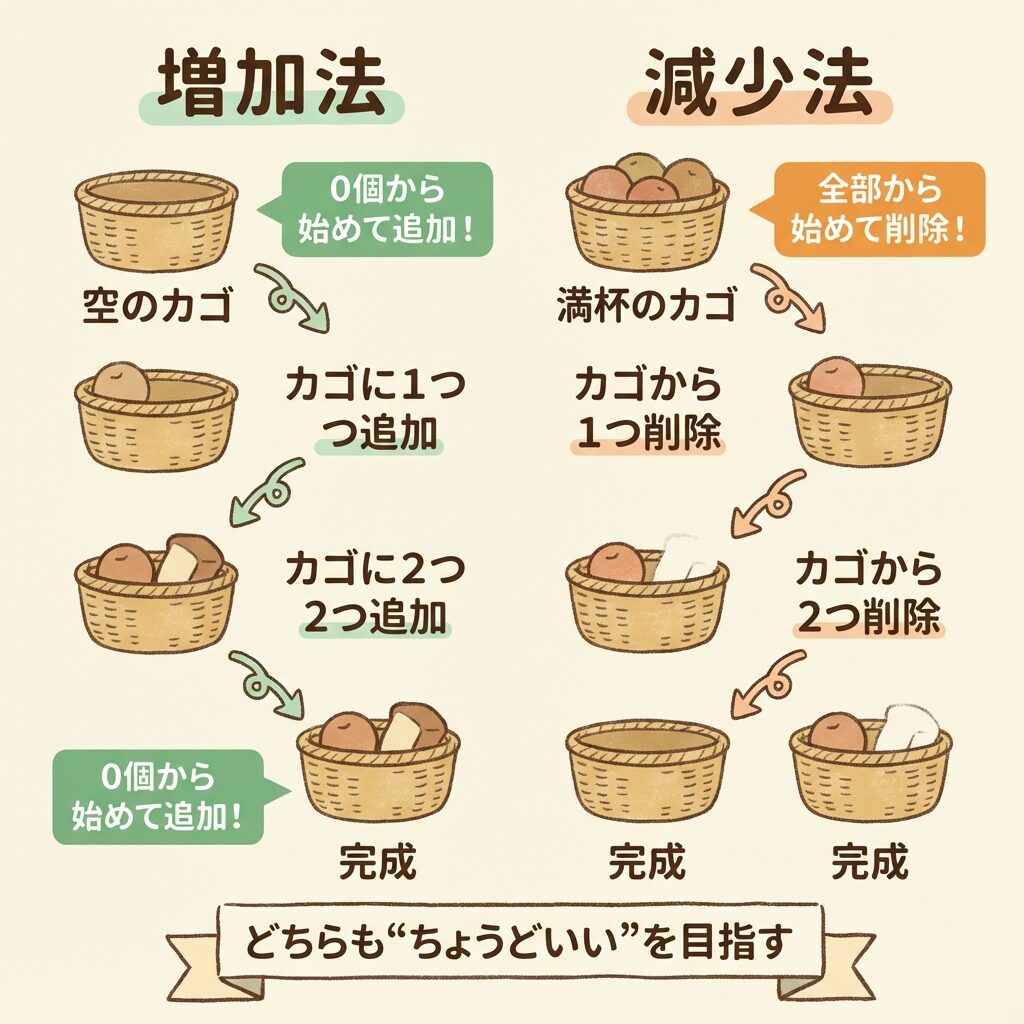
「過少適合」と「過学習」のちょうど真ん中を見つけること。
必要な変数だけを残し、不要な変数を取り除く。

変数選択の3つの方法
変数選択には、大きく分けて3つの方法があります。
| 方法 | イメージ | 特徴 |
|---|---|---|
| 増加法 (Forward) |
0個から始めて 1つずつ追加 |
シンプル、計算が速い |
| 減少法 (Backward) |
全部入れてから 1つずつ削除 |
変数間の関係を考慮できる |
| ステップワイズ法 (Stepwise) |
追加と削除を 繰り返す |
最もよく使われる |
それぞれ詳しく見ていきましょう。
方法①:増加法(Forward Selection)
増加法は、変数0個の状態から始めて、1つずつ追加していく方法です。
空のカゴを持ってスーパーに行きます。
「これは本当に必要?」と確認しながら、
必要なものだけを1つずつカゴに入れていくイメージです。
増加法の手順
Step 1:変数なしのモデル(定数項のみ)から開始
Step 2:各変数を1つずつ追加したモデルを作り、どれが最も改善するか調べる
Step 3:最も改善する変数が「有意」なら追加。有意でなければ終了
Step 4:Step 2〜3を繰り返す
増加法の具体例
候補変数が x₁, x₂, x₃ の3つあるとします。
| ステップ | 試すモデル | 結果 |
|---|---|---|
| 1 | y ~ x₁ / y ~ x₂ / y ~ x₃ | x₁が最も改善 → x₁を追加 |
| 2 | y ~ x₁ + x₂ / y ~ x₁ + x₃ | x₃が有意に改善 → x₃を追加 |
| 3 | y ~ x₁ + x₃ + x₂ | x₂は有意でない → 終了 |
結果:y = b₀ + b₁x₁ + b₃x₃ が最終モデル
方法②:減少法(Backward Elimination)
減少法は、全変数を入れた状態から始めて、1つずつ削除していく方法です。
クローゼットの服を全部出します。
「これは本当に必要?」と確認しながら、
不要なものを1つずつ捨てていくイメージです。
減少法の手順
Step 1:全変数を入れたモデルから開始
Step 2:各変数を1つずつ削除したモデルを作り、どれが最も不要か調べる
Step 3:最も不要な変数(t検定で有意でない変数)を削除。すべて有意なら終了
Step 4:Step 2〜3を繰り返す
減少法の具体例
| ステップ | 現在のモデル | 結果 |
|---|---|---|
| 1 | y ~ x₁ + x₂ + x₃ | x₂が最も有意でない → x₂を削除 |
| 2 | y ~ x₁ + x₃ | x₁, x₃ ともに有意 → 終了 |
結果:y = b₀ + b₁x₁ + b₃x₃ が最終モデル(増加法と同じ結果)
今回はたまたま同じ結果になりましたが、必ずしも一致するとは限りません。
変数間の相関関係によっては、異なる結果になることがあります。
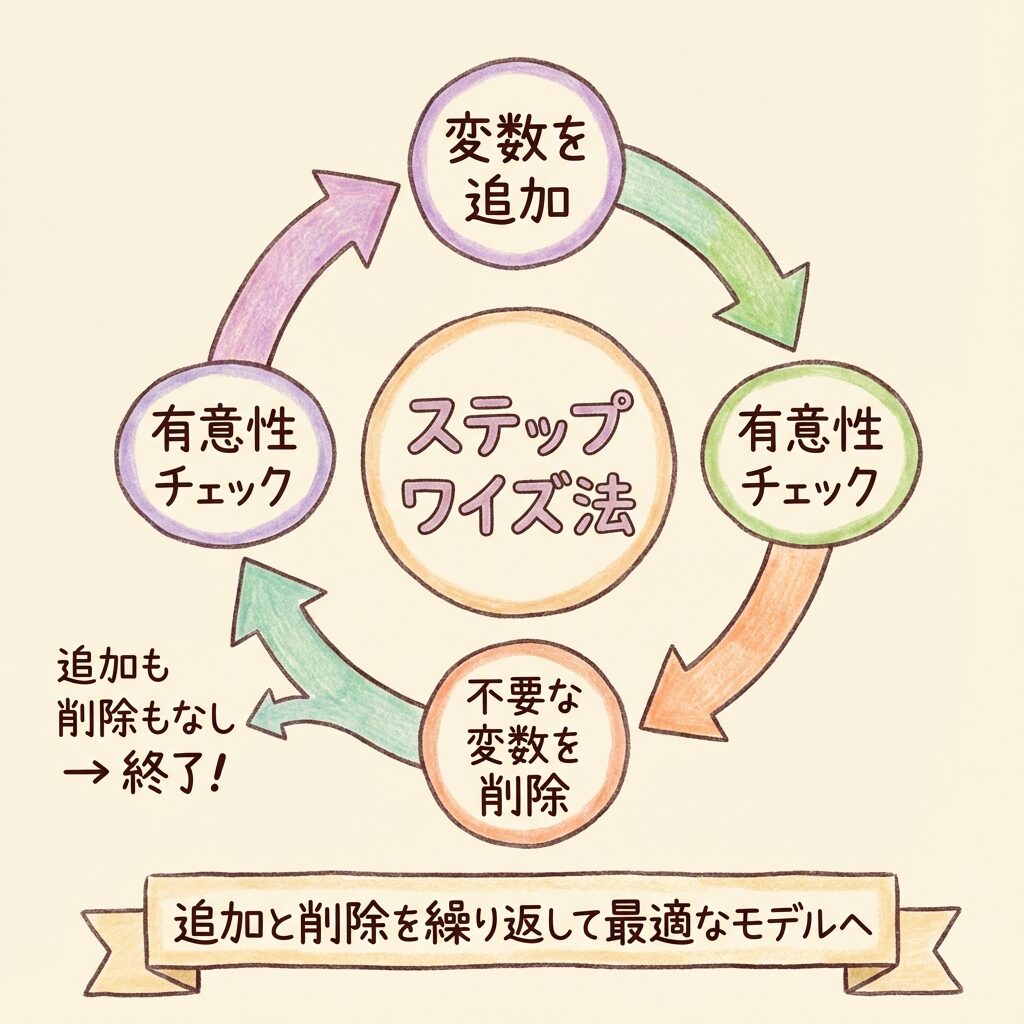
方法③:ステップワイズ法(Stepwise Selection)
ステップワイズ法は、追加と削除を両方行う方法です。増加法と減少法の「いいとこ取り」ですね。
最もよく使われる変数選択法で、多くの統計ソフトのデフォルト設定になっています。
サッカーチームを作っています。
・新しい選手をスカウト(追加)しつつ
・活躍していない選手を放出(削除)する
追加と削除を繰り返して、最強のチームを目指します。
ステップワイズ法の手順
Step 1:変数なし、または全変数から開始(設定による)
Step 2:追加候補の中で最も改善する変数を探す
Step 3:追加したら、既存の変数で不要になったものがないか確認
Step 4:不要な変数があれば削除
Step 5:追加も削除もできなくなったら終了
なぜ「追加後に削除」が必要?
「追加した変数をまた削除するの?無駄じゃない?」と思うかもしれません。
実は、新しい変数を追加すると、既存の変数が不要になることがあるんです。
最初:x₁だけのモデル → x₁は有意
次に:x₃を追加 → x₁とx₃が似ているため、x₁が有意でなくなる
結果:x₁を削除して、x₃だけのモデルになる
このような「入れ替わり」が起こりうるので、追加後の削除チェックが重要なのです。
3つの方法の比較
| 方法 | メリット | デメリット | おすすめ度 |
|---|---|---|---|
| 増加法 | 計算が速い | 一度入れた変数は削除されない | ★★☆ |
| 減少法 | 変数間の関係を考慮 | 変数が多いと計算が重い | ★★☆ |
| ステップワイズ法 | 柔軟性が高い | 最適解とは限らない | ★★★ |
迷ったらステップワイズ法を選びましょう。
最も柔軟で、多くの場面で良い結果を出してくれます。
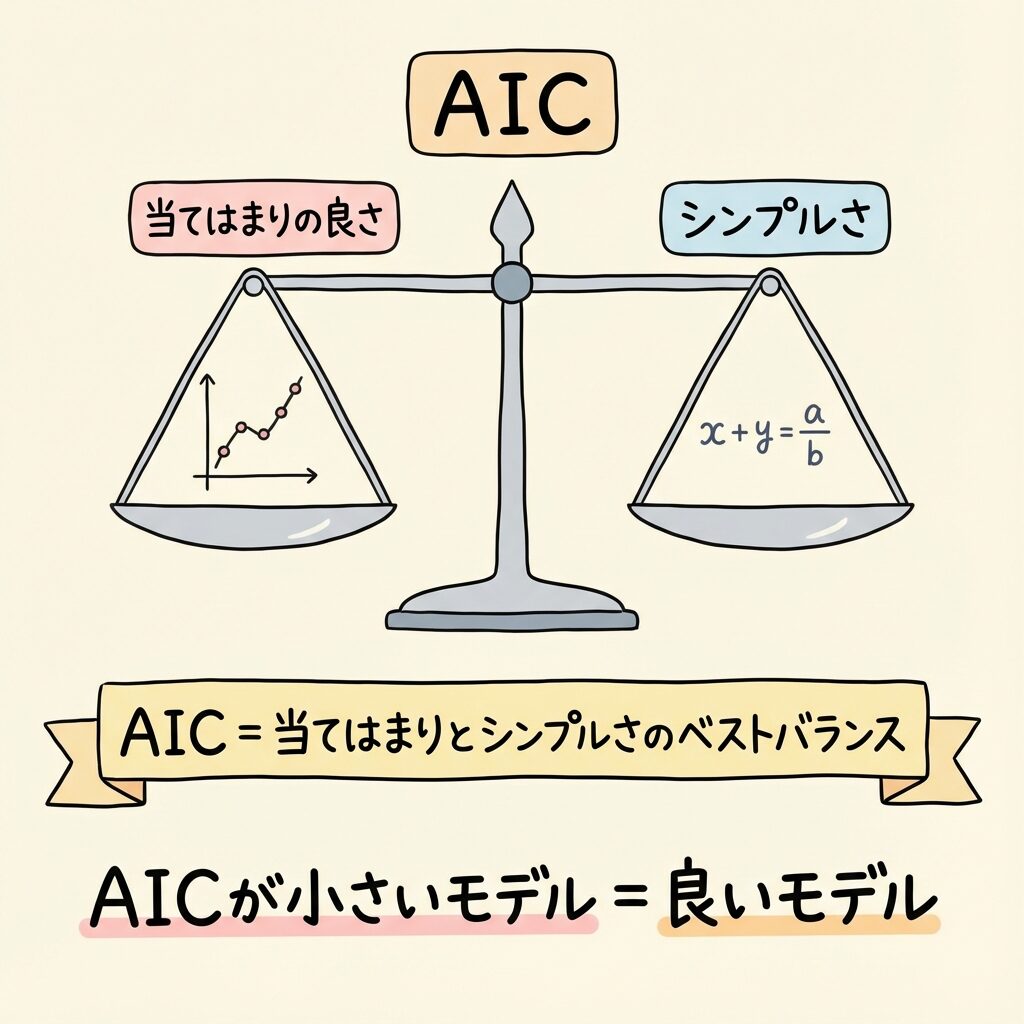
AIC(赤池情報量基準)とは?
「当てはまり」と「シンプルさ」のバランスを測る指標
ここまでの方法は、「有意かどうか」でp値を基準に判断していました。
でも、もっと便利な指標があります。それがAIC(Akaike Information Criterion:赤池情報量基準)です。
AICは、日本の統計学者・赤池弘次さんが1970年代に提唱した指標で、世界中で使われています。
AIC = 当てはまりの悪さ + 複雑さへのペナルティ
AICが小さいモデルほど「良いモデル」
AICは2つの要素のバランスを取っています。
| 要素 | 意味 | 変数を増やすと… |
|---|---|---|
| 当てはまりの悪さ | データへのフィット度合い (残差の大きさ) |
↓ 減る(良くなる) |
| 複雑さへのペナルティ | 変数の数に対する罰則 (2 × 変数の数) |
↑ 増える(悪くなる) |
変数を増やすと「当てはまり」は良くなりますが、「ペナルティ」も増えます。このトレードオフのバランスが最も良いモデルを選ぶのがAICの考え方です。
AICを「食べ放題」で例えると…
食べ放題に来ました。
・料理の満足度(当てはまりの良さ)を上げたい
・でも食べすぎると胃もたれ(複雑さのペナルティ)
「満足度が高く、胃もたれしない」ちょうどいい量を見つけるのがAICです。
たくさん食べれば満足度は上がるけど、胃もたれもする。
トータルで最も快適な量を選ぶイメージ。
AICの計算式
最大対数尤度:モデルがデータをどれだけうまく説明できるか
パラメータ数:偏回帰係数の数 + 1(切片)
計算式は複雑に見えますが、実際には統計ソフトが自動で計算してくれます。
大切なのは、AICが小さいモデルを選ぶということだけ覚えておけばOKです。
AICによる変数選択の例
いくつかのモデルを比較してみましょう。
| モデル | 変数 | AIC | 判定 |
|---|---|---|---|
| モデルA | x₁のみ | 152.3 | |
| モデルB | x₁ + x₃ | 138.7 | 最小 ✓ |
| モデルC | x₁ + x₂ + x₃ | 140.2 |
モデルB(x₁ + x₃)のAICが最も小さいので、これが最適なモデルと判断できます。
モデルCは変数を1つ追加していますが、AICは増えています。これは「x₂を追加しても、ペナルティ分ほどは当てはまりが改善しなかった」ということです。
p値とAIC、どちらを使うべき?
目的によって使い分ける
「p値(有意性検定)とAIC、どっちを使えばいいの?」という疑問があるかもしれません。
答えは、「目的によって使い分ける」です。
| 目的 | おすすめの基準 | 理由 |
|---|---|---|
| 因果関係を調べたい | p値 | 「この変数は本当に効いているか」を統計的に証明できる |
| 予測精度を上げたい | AIC | 新しいデータでの予測性能を重視できる |
| どちらも大事 | 両方使う | AICで候補を絞り、p値で最終確認 |
まずはAICでモデルを選び、その後p値で各変数の有意性を確認する、という流れがおすすめです。
AICで選んだモデルの変数がすべて有意なら、そのモデルを採用。
有意でない変数があれば、削除を検討します。
変数選択の注意点
注意①:理論的な重要性も考慮する
統計的な基準だけで変数を選ぶのは危険です。
たとえば、「年齢」は売上に影響していると理論的にわかっているのに、たまたま今回のデータでは有意にならなかった、ということがあります。
そんなとき、「有意じゃないから削除」と機械的に判断してはいけません。理論的に重要な変数は、有意でなくても残すことがあります。
注意②:多重共線性をチェックする
変数選択の前に、多重共線性(VIF)をチェックしましょう。
相関の高い変数が両方入っていると、変数選択の結果が不安定になります。VIFが高い変数は、事前に1つに絞っておくのがベターです。
注意③:最適解とは限らない
ステップワイズ法などの逐次的な方法は、「局所最適解」に陥ることがあります。
つまり、「今いる場所からは一番いいけど、もっと遠くにさらに良い場所がある」という状況です。
可能であれば、全通りの組み合わせを試す「総当たり法」が最も確実です。ただし、変数が多いと計算量が爆発するので、現実的には難しいこともあります。
変数選択は「正解」を見つける方法ではありません。
「より良いモデル」を見つける手段です。
最終的には、理論的な妥当性と統計的な基準の両方を考慮して判断しましょう。
まとめ
この記事では、変数選択の方法について解説しました。
- 変数が多すぎると過学習、少なすぎると過少適合
- 増加法:0個から追加していく
- 減少法:全部から削除していく
- ステップワイズ法:追加と削除を繰り返す(最もよく使われる)
- AIC:当てはまりとシンプルさのバランス。小さいほど良いモデル
- 統計的基準だけでなく、理論的な重要性も考慮する
変数選択をマスターしたら、次は相関分析の統計的検定について学びましょう。
📚 次に読むべき記事
相関係数が「偶然」でないことを証明する方法
変数選択の前にチェックすべき重要な指標
重回帰分析の基礎から復習したい方へ