- 「分散って何?なんで2乗するの?」
- 「標準偏差と分散の違いがわからない…」
- 「公式は覚えたけど、意味がわからない」
- 「V(X) = E(X²) - μ² って、どこから出てきたの?」
統計学で最も重要な概念の一つが「分散」と「標準偏差」です。
でも、いきなり「偏差を2乗して平均を取る」と言われても、「なんで2乗?」「なんで平均?」と疑問だらけですよね。
この記事では、「なぜこの公式になるのか」を徹底的に図解します。読み終わる頃には、分散と標準偏差が「当たり前」に感じられるようになります!
- 分散=データの「バラつき」を数値化したもの
- 標準偏差=分散の平方根(元の単位に戻したもの)
- 偏差を2乗する理由=プラスマイナスを相殺させないため
- 計算公式V(X) = E(X²) - μ²の導出も完全理解
目次
🎯 そもそも「バラつき」とは?
まず、「バラつき」が何を意味するのか、具体例で確認しましょう。
2つのクラスのテスト結果を比べてみます。どちらも平均点は60点です。
| クラス | 生徒A | 生徒B | 生徒C | 生徒D | 生徒E | 平均 |
|---|---|---|---|---|---|---|
| 1組 | 58 | 59 | 60 | 61 | 62 | 60点 |
| 2組 | 20 | 40 | 60 | 80 | 100 | 60点 |
どちらも平均は同じ60点です。でも、明らかに「性格」が違いますよね。
1組は全員が60点付近に集まっていて、バラつきが小さい。
2組は20点から100点まで散らばっていて、バラつきが大きい。
この「バラつき」を数値化したものが、分散と標準偏差なんです。
📏 偏差とは?「平均からの距離」
バラつきを測るには、まず「各データが平均からどれだけ離れているか」を調べます。
この「平均からの距離」を偏差(へんさ)と呼びます。
偏差 = データの値 − 平均値 = X − μ
2組の偏差を計算してみましょう(平均μ = 60)。
| 生徒 | 点数 X | 偏差 (X − μ) |
|---|---|---|
| A | 20 | −40 |
| B | 40 | −20 |
| C | 60 | 0 |
| D | 80 | +20 |
| E | 100 | +40 |
| 偏差の合計 | 0 | |
❌ 問題発生!偏差の合計は必ず0になる
上の表を見てください。偏差の合計が0になっています!
これは偶然ではありません。偏差の合計は「必ず」0になるという性質があるんです。
平均値は「シーソーの支点」のようなものです。
支点より左(マイナス)と右(プラス)の力は、必ず釣り合います。
だから、偏差を単純に足し算すると0になって消えてしまうんです。
これでは「バラつき」が測れません。どうすればいいでしょうか?
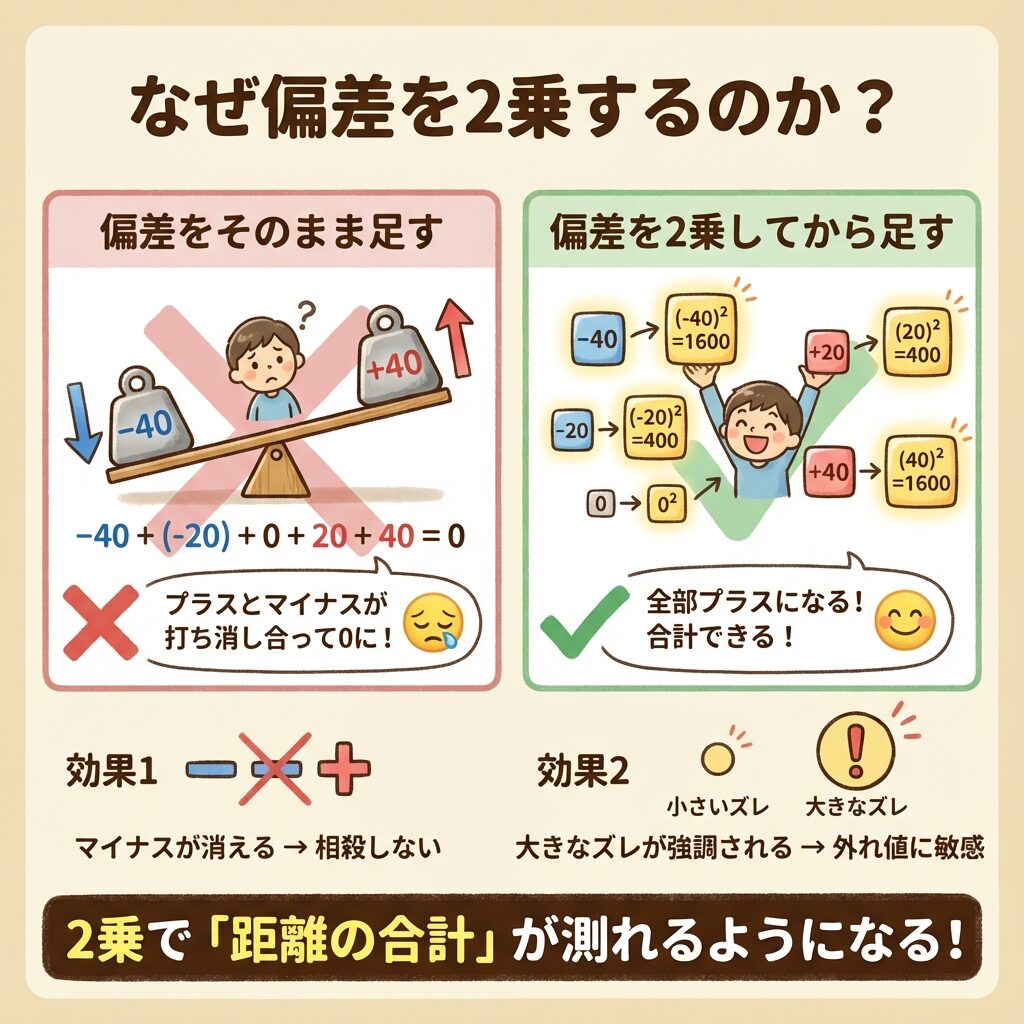
🔢 なぜ「2乗」するのか?
プラスとマイナスが打ち消し合う問題を解決するために、偏差を2乗します。
✅ 2乗の効果①:マイナスが消える
どんな数も2乗するとプラスになります。
(−40)² = 1600 (マイナスが消える!)
(+40)² = 1600 (同じ値になる!)
✅ 2乗の効果②:大きなズレが強調される
2乗すると、平均から遠いデータほど、より大きな値になります。
| 偏差 | 偏差² | 倍率 |
|---|---|---|
| 10 | 100 | 10倍 |
| 20 | 400 | 20倍 |
| 40 | 1600 | 40倍 |
偏差が2倍になると、偏差²は4倍になります。つまり、「外れ値」が強調されるんです。
「マイナスを消すなら絶対値でもいいのでは?」と思うかもしれません。
実は、2乗には数学的に扱いやすいという大きなメリットがあります。
微分がしやすく、他の統計量との相性も抜群なんです。
📊 分散の定義式
偏差の2乗を平均したものが、「分散」です。
V(X) = E{(X − μ)²} = σ²
V(X):分散 E{ }:期待値(平均) μ:平均値 σ²:分散の別表記
言葉で言うと、「偏差の2乗の期待値(平均)」です。
🧮 2組の分散を計算してみよう
| 生徒 | 点数 X | 偏差 (X − μ) | 偏差² (X − μ)² |
|---|---|---|---|
| A | 20 | −40 | 1600 |
| B | 40 | −20 | 400 |
| C | 60 | 0 | 0 |
| D | 80 | +20 | 400 |
| E | 100 | +40 | 1600 |
| 合計 | 4000 | ||
分散 V(X) = 4000 ÷ 5 = 800
2組の分散は800です。1組の分散は計算すると2になります。
分散が大きいほど「バラつきが大きい」ことを表しています。
🔥 計算公式の導出|V(X) = E(X²) − μ²
実務では、上の定義式よりも計算しやすい公式がよく使われます。
V(X) = E(X²) − μ²
「X²の期待値」から「平均の2乗」を引く
この公式は、定義式から数学的に導出できます。QC検定や統計検定でも頻出なので、導出過程を理解しておきましょう。
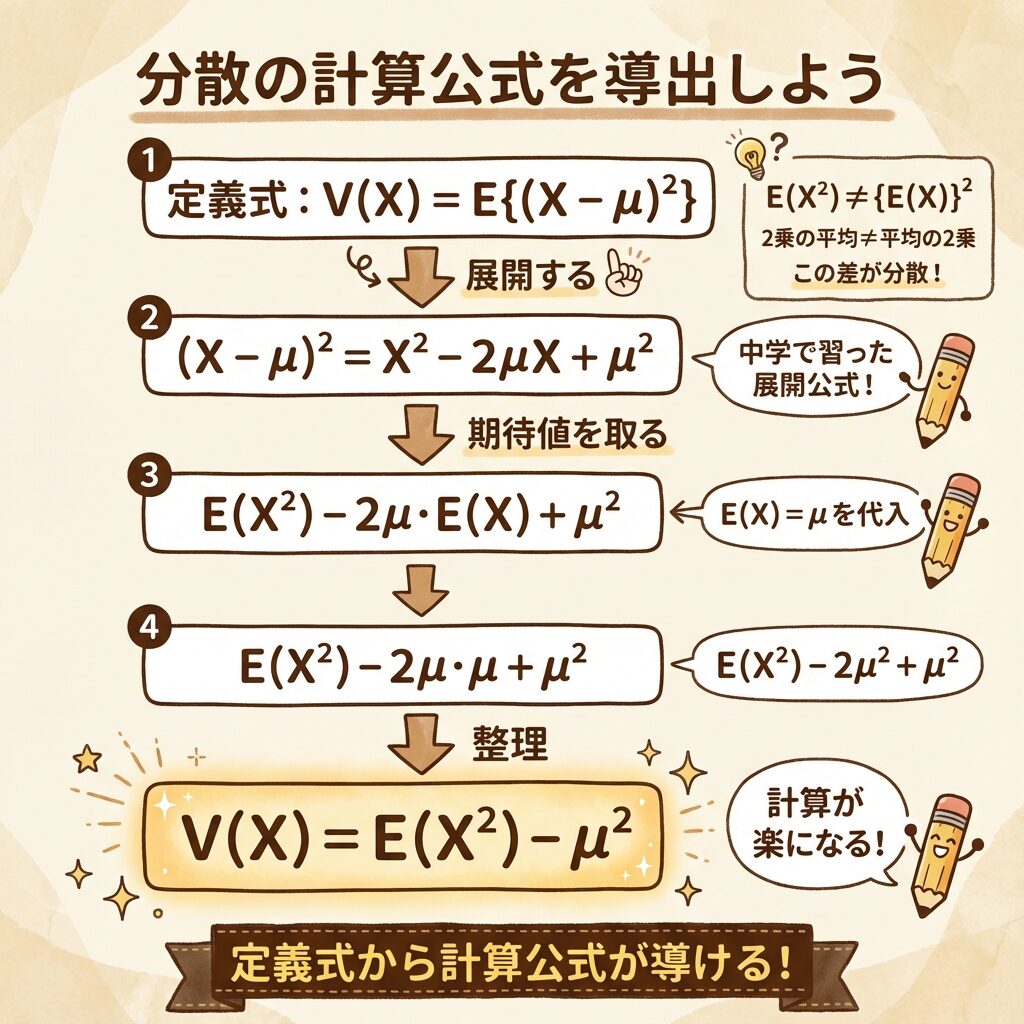
📝 導出の手順
定義式から始めます。
Step 1:定義式を書く
V(X) = E{(X − μ)²}
Step 2:カッコの中を展開する
(X − μ)² = X² − 2μX + μ²
Step 3:期待値を取る
V(X) = E(X² − 2μX + μ²)
Step 4:期待値の線形性を使って分解
V(X) = E(X²) − 2μ·E(X) + μ²
Step 5:E(X) = μ を代入
V(X) = E(X²) − 2μ·μ + μ²
V(X) = E(X²) − 2μ² + μ²
Step 6:整理して完成!
V(X) = E(X²) − μ²
E(X²):「データの2乗」の平均
μ²:「データの平均」の2乗
この2つの差が分散です。
「2乗の平均」と「平均の2乗」は違う、ということがポイント!
第8回:期待値 - 確率分布の中心を知る →
📏 標準偏差とは?「元の単位に戻す」
分散には一つ問題があります。それは単位が2乗になってしまうことです。
例えば、テストの点数(単位:点)の分散は「点²(点の2乗)」になります。これでは直感的にわかりにくいですよね。
そこで、分散の平方根を取って、元の単位に戻したものが「標準偏差」です。
D(X) = √V(X) = √E{(X − μ)²} = σ
D(X):標準偏差 σ(シグマ):標準偏差の記号
🧮 標準偏差を計算してみよう
2組の標準偏差を計算します。
分散 V(X) = 800
標準偏差 σ = √800 ≒ 28.3点
標準偏差は「約28点」です。これなら「平均から約28点くらいバラついている」と直感的に理解できますね!
📊 分散と標準偏差の使い分け
| 項目 | 分散 σ² | 標準偏差 σ |
|---|---|---|
| 単位 | 元のデータの2乗 | 元のデータと同じ |
| 直感的理解 | △ わかりにくい | ◎ わかりやすい |
| 計算 | ◎ 楽(加法性あり) | △ ルートが必要 |
| 主な用途 | 数学的計算、検定 | 報告、グラフ、解釈 |
🎯 標準偏差の「68-95-99.7ルール」
正規分布に従うデータでは、標準偏差を使って「何%のデータがこの範囲に入る」と予測できます。
| 範囲 | データの割合 |
|---|---|
| μ ± 1σ | 約68% |
| μ ± 2σ | 約95% |
| μ ± 3σ | 約99.7% |
つまり、平均±2標準偏差の範囲に、ほぼ全員(95%)が入るということです。

📚 まとめ|分散と標準偏差の要点
- 分散=偏差の2乗の平均 → V(X) = E{(X − μ)²}
- 標準偏差=分散の平方根 → σ = √V(X)
- 偏差を2乗する理由=プラスマイナスの相殺を防ぐ&外れ値を強調
- 計算公式:V(X) = E(X²) − μ²
- 正規分布ではμ±2σに95%のデータが入る
| 分散(定義式) | V(X) = E{(X − μ)²} = σ² |
| 分散(計算公式) | V(X) = E(X²) − μ² |
| 標準偏差 | D(X) = √V(X) = σ |
- V(X) = E(X²) − μ² の導出過程が出題される
- 「2乗の期待値」と「期待値の2乗」の違いを理解
- 分散と標準偏差の単位の違いに注意
- 分散の加法性(独立な変数の分散は足せる)も重要
📖 統計学基礎シリーズ
第9回:分散の加法性 - 独立な確率変数の性質 →
分散と標準偏差は「バラつきを数値化する魔法の道具」でしたね。
偏差を2乗する理由、計算公式の導出まで理解できれば、
統計学の土台がしっかり固まります!
次は「データの視覚化」を学びましょう!📊📏
