- ヒストグラムって何?棒グラフと何が違うの?
- 度数分布表の作り方がわからない
- 階級数や階級幅ってどう決めればいいの?
- グラフの「形」から何を読み取ればいいの?
- ヒストグラムの意味と棒グラフとの決定的な違い
- 度数分布表の作り方(6ステップで完全マスター)
- 階級数を決める「スタージェスの公式」
- 分布の形(正規分布・歪み・二峰性)の見分け方
「平均点は65点です」
この情報だけで、クラスの様子がわかりますか?
全員が60〜70点に集まっているのか、0点と100点が半分ずついるのか——平均値だけでは、データの「本当の姿」は見えません。
そこで登場するのが「ヒストグラム」です。
ヒストグラムは、データを「絵」にすることで、数字の羅列が「形」として見えるようになる魔法のグラフ。統計分析の第一歩は、まずヒストグラムを描くことから始まります。
この記事では、ヒストグラムの作り方から読み方まで、統計初心者でも「完全に理解できる」レベルで徹底解説します。
目次
ヒストグラムとは?|データの「形」を見るグラフ
まず、ヒストグラムの基本を押さえましょう。
ヒストグラムの定義
データを一定の区間(階級)に分け、各区間に入るデータの個数(度数)を柱の高さで表したグラフ。データの「散らばり具合(分布)」を視覚的に把握できる。
難しく聞こえますか?大丈夫です。たとえ話で説明しましょう。
30人の学生のテスト結果(0〜100点)があるとします。
これを10階建てのマンションに例えると…
・1階:0〜9点の人(0人)
・2階:10〜19点の人(1人)
・3階:20〜29点の人(2人)
・4階:30〜39点の人(3人)
・…
・10階:90〜100点の人(2人)
各階に何人いるかを棒の高さで表したのがヒストグラムです。
つまり、ヒストグラムは「データをグループ分けして、各グループの人数を数えたもの」です。
なぜヒストグラムが必要なのか?
「平均値」や「標準偏差」だけでは見えない情報があります。
クラスA:全員が65点前後 → 平均65点
クラスB:30点が半分、100点が半分 → 平均65点
どちらも「平均65点」ですが、データの姿は全く違います。
ヒストグラムを描けば、この違いが一目でわかります。
だから、データ分析の鉄則は「まずヒストグラムを描く」なのです。
第3回:平均値の奥深い世界 →
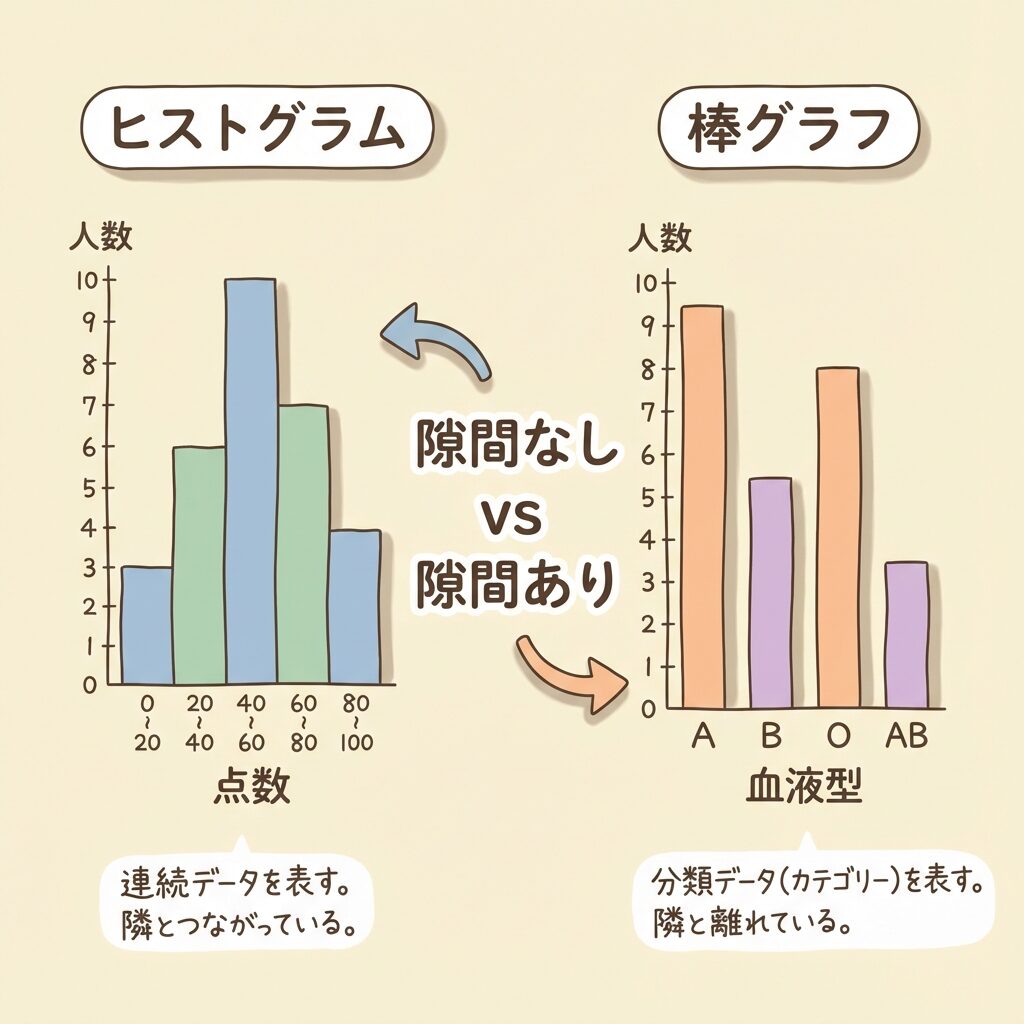
ヒストグラムと棒グラフの違い|ここを間違えると恥ずかしい!
「ヒストグラムと棒グラフって同じじゃないの?」
これは初心者がよくやる間違いです。見た目は似ていますが、全く違うグラフなんです。
決定的な3つの違い
| 比較項目 | ヒストグラム | 棒グラフ |
|---|---|---|
| 扱うデータ | 連続データ(数値) | カテゴリデータ |
| 横軸 | 数値の範囲(0〜10、10〜20…) | 項目の名前(A型、B型…) |
| 柱の隙間 | 隙間なし(連続性を表す) | 隙間あり(独立した項目) |
| 並び替え | できない(順序に意味あり) | できる(順序に意味なし) |
「柱に隙間があるか?」を見ればOK!
・隙間なし → ヒストグラム
・隙間あり → 棒グラフ
ヒストグラムは「連続するデータ」を扱うので、柱も連続して(くっついて)いるのです。
具体例で理解する
| グラフの種類 | 使う場面の例 |
|---|---|
| ヒストグラム | テストの点数分布、身長の分布、製品の寸法分布、待ち時間の分布 |
| 棒グラフ | 血液型の人数、都道府県別の人口、好きな果物ランキング |
この違いを理解していないと、レポートや発表で「この人、統計わかってないな…」と思われてしまいます。しっかり区別しましょう!
第2回:データの種類を完全理解 - 4つの尺度 →
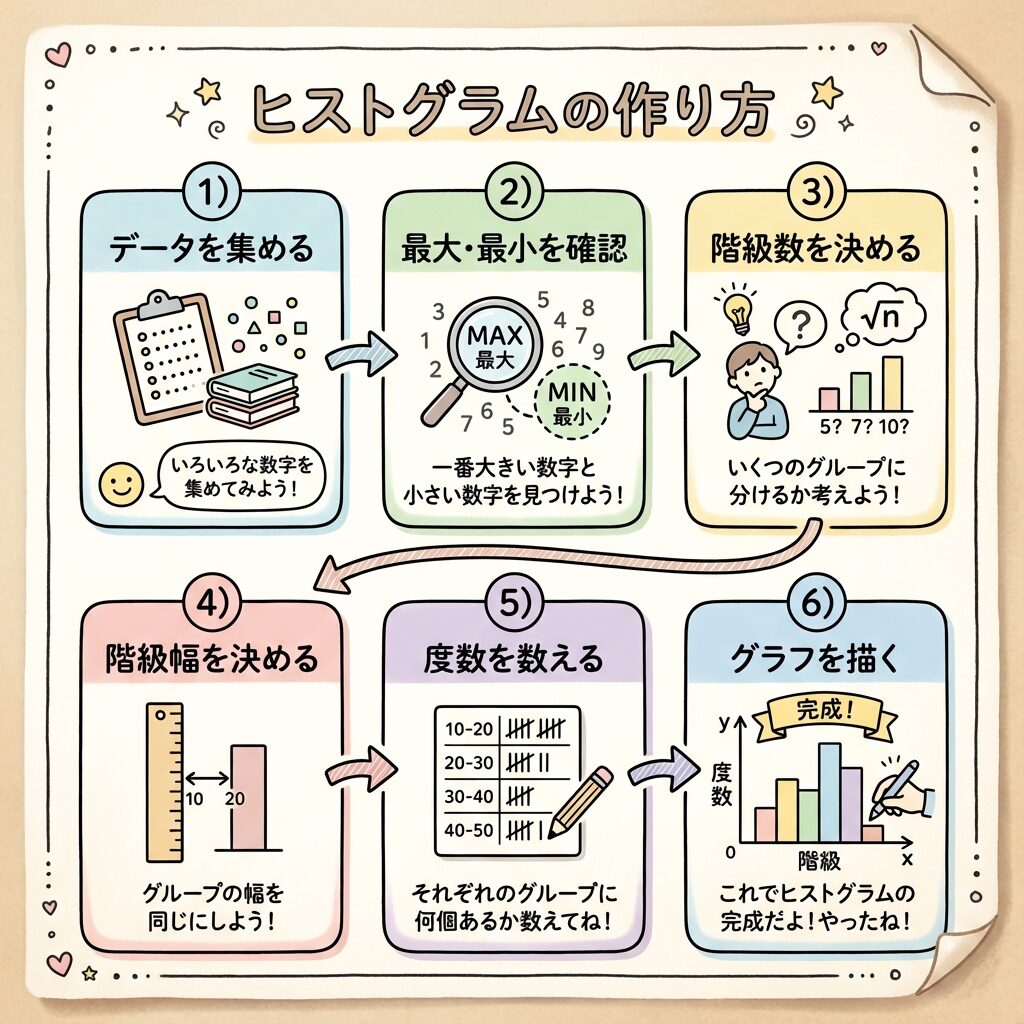
ヒストグラムの作り方|6ステップで完全マスター
ここからは、実際にヒストグラムを作る手順を解説します。30人のテスト結果を例に、一緒に作ってみましょう。
52, 58, 61, 63, 65, 67, 68, 70, 71, 72,
73, 74, 75, 76, 77, 78, 79, 80, 81, 82,
83, 84, 85, 86, 87, 88, 89, 91, 93, 95
STEP 1:データの範囲(レンジ)を確認する
まず、データの最大値と最小値を確認します。
・最小値:52点
・範囲(レンジ):95 - 52 = 43点
この「43点」の幅をどう区切るかが、次のステップです。
STEP 2:階級数(柱の本数)を決める
「何本の柱に分けるか」を決めます。ここで便利なのが「スタージェスの公式」です。
階級数 ≒ 1 + log₂(データ数)
「log₂って何?」と思った方、安心してください。以下の早見表を使えばOKです。
| データ数 | 推奨階級数 |
|---|---|
| 10〜20個 | 5本 |
| 20〜40個 | 6本 |
| 40〜80個 | 7本 |
| 80〜160個 | 8本 |
| 160〜320個 | 9本 |
今回はデータが30個なので、階級数は約6本が目安です。
STEP 3:階級の幅を決める
範囲(43点)を階級数(6本)で割ります。
→ キリの良い数字にして「8点刻み」にしよう!
計算結果をそのまま使うより、「5」「10」「8」などキリの良い数字にすると、グラフが読みやすくなります。
STEP 4:階級の境界を決める
最小値(52点)を含むように、階級の境界を決めます。
50点からスタートして、8点刻みで区切ると…
- 50〜58点
- 58〜66点
- 66〜74点
- 74〜82点
- 82〜90点
- 90〜98点
STEP 5:度数(人数)を数える
各階級に何人いるかを数えて、度数分布表を作ります。
| 階級(点数) | 度数(人数) |
|---|---|
| 50〜58 | 2人 |
| 58〜66 | 4人 |
| 66〜74 | 6人 |
| 74〜82 | 10人(最多!) |
| 82〜90 | 6人 |
| 90〜98 | 2人 |
STEP 6:グラフを描く
横軸に「点数」、縦軸に「人数」をとって、柱を立てれば完成です!
- 山のピーク:74〜82点に最も多い(10人)
- 分布の形:中央が高く、両端が低い → ほぼ正規分布に近い
- 解釈:このテストは適切な難易度で、多くの生徒が平均付近に集まっている
階級幅を狭くしすぎると、ギザギザになって全体像が見えなくなります。
逆に広くしすぎると、ただの四角になって分布の特徴が消えます。
「データの全体像が一番つかめる幅」を探す試行錯誤が大切です。
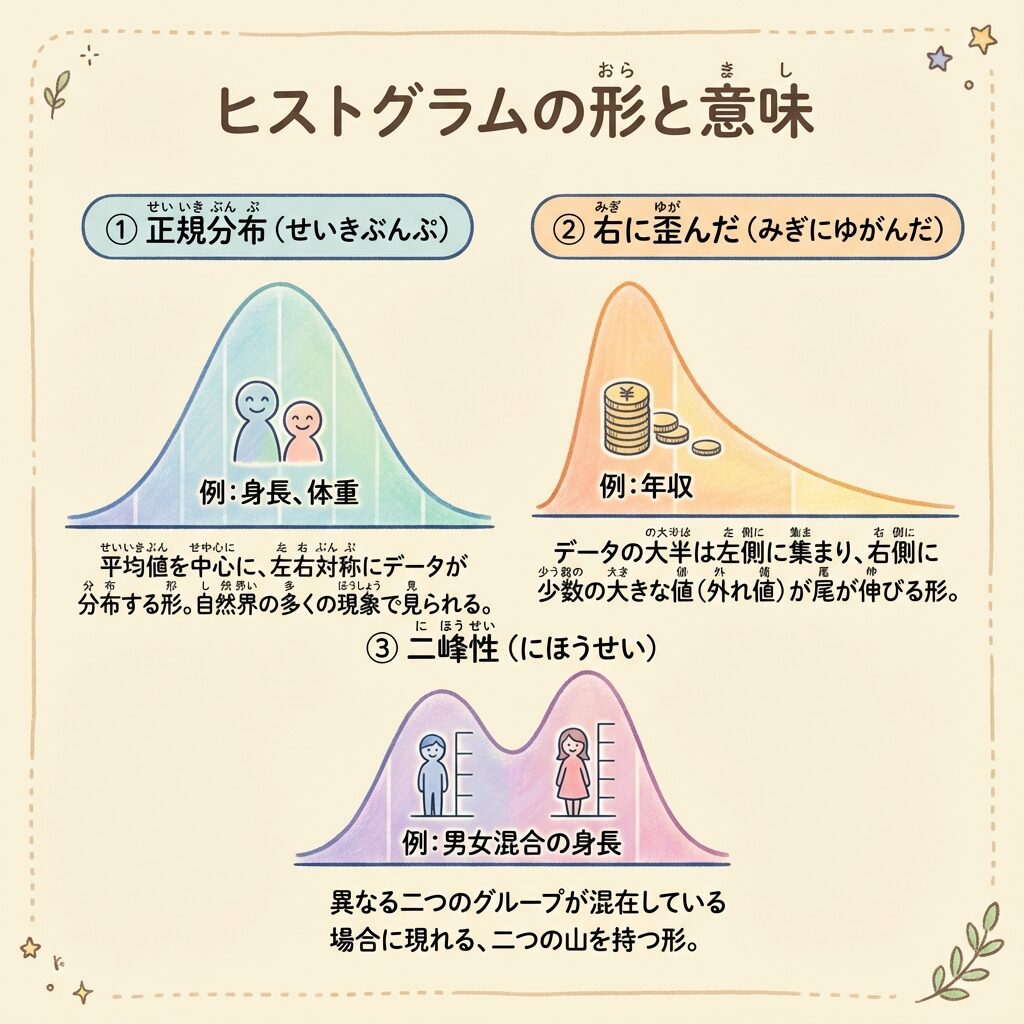
分布の形を読み解く|3つの代表的なパターン
ヒストグラムを描いたら、次は「山の形」を読む番です。形から、データの背後にある「ストーリー」が見えてきます。
パターン①:正規分布(ベル型)🔔
・特徴:左右対称のきれいな釣鐘型
・意味:平均付近にデータが集まり、極端な値は少ない
・例:身長、体重、測定誤差、IQ
自然界や人間の特性は、多くの場合この形になります。統計学で最も重要な分布です。
パターン②:右に歪んだ分布(右裾が長い)📉
・特徴:左に山があり、右に長い尻尾が伸びる
・意味:「桁外れに大きい値」を持つ少数のデータがある
・例:年収、貯蓄額、企業の売上、SNSのフォロワー数
日本人の年収分布を見ると、300〜500万円あたりに山があり、右側に長い尻尾が伸びています。
これは「年収1億円以上」という少数の超高収入者が、平均を引き上げているから。
こういうデータでは、「平均」より「中央値」の方が実態を表します。
第4回:中央値と最頻値 - 平均以外の代表値 →
パターン③:二峰性(ふたこぶラクダ型)🐫
・特徴:山が2つある
・意味:「2つの異なる集団」が混ざっているサイン!
・例:男女混合の身長データ、昼シフトと夜シフトの生産データ
二峰性は「データを分けて分析すべき」というサインです。
例:製品の不良率が二峰性だった場合
→ 「昼のシフトと夜のシフトで作り方が違うのでは?」
→ 「材料Aと材料Bが混ざっていないか?」
原因を探って、データを分離してから分析しましょう。
分布の形の比較まとめ
| 分布の形 | 特徴 | 代表例 | 使うべき代表値 |
|---|---|---|---|
| 正規分布 | 左右対称 | 身長、体重 | 平均値 |
| 右に歪み | 右に尻尾 | 年収、貯蓄 | 中央値 |
| 二峰性 | 山が2つ | 男女混合データ | 分離して分析 |
実践:ヒストグラムから「ストーリー」を読む
ヒストグラムは「描いて終わり」ではありません。グラフから「なぜそうなったか?」を読み取ることが本当の目的です。
ケース1:テスト結果が「左に歪んでいる」
右(高得点)に山があり、左(低得点)に長い尻尾がある。
考えられる解釈:
- 「テストが簡単すぎた」(多くの人が高得点を取れた)
- 「勉強不足の生徒が一部だけいた」(低得点者が少数)
- 次回は「難易度を上げるべき」という示唆
ケース2:製品の寸法が「二峰性」
山が2つある。
考えられる解釈:
- 「2つの異なる条件で製造されたデータが混ざっている」
- 例:機械Aと機械Bで結果が違う、昼シフトと夜シフトで違う
- データを分離して、それぞれ分析すべき
製造業では、ヒストグラムは「QC7つ道具」の一つとして重宝されています。
不良が発生したとき、まずヒストグラムを描いて「分布の形」を確認する。
二峰性が出れば「原因は2種類ある」と推測でき、調査の方向性が見えます。
ヒストグラムをExcelで作る方法
手書きで作るのは大変ですよね。Excelなら簡単にヒストグラムを作れます。
- データを入力する
- 「挿入」タブ → 「統計グラフの挿入」 → 「ヒストグラム」を選択
- グラフをクリックして「ビンの幅」(=階級幅)を調整
- 完成!
Excel 2016以降なら、「ヒストグラム」が標準機能として使えます。ぜひ試してみてください。

まとめ:まずヒストグラムを描く習慣をつけよう
最後に、この記事のポイントをまとめます。
- ヒストグラムは、データの「散らばり具合(分布)」を視覚化するグラフ
- 棒グラフとの違い:ヒストグラムは「隙間なし」「連続データ」を扱う
- 階級数の目安:スタージェスの公式(データ30個なら約6本)
- 階級幅のコツ:キリの良い数字(5、8、10など)にすると見やすい
- 分布の形:正規分布(左右対称)、右に歪み、二峰性(山が2つ)
- 二峰性が出たら「2つの集団が混ざっている」サイン → 分離して分析
- 分析の第一歩:平均を計算する前に、まずヒストグラムを描く!
「平均値」「標準偏差」などの数値は、データを要約するのに便利です。しかし、数値だけでは見えない情報がたくさんあります。
ヒストグラムを描けば、データの「形」が見える。形が見えれば、その背後にある「ストーリー」が見えてくる。
「データを見たら、まずヒストグラムを描く」——この習慣をつけるだけで、あなたのデータ分析力は格段に向上します。
データの分布が分かると、次に気になるのは「この結果は偶然なのか?必然なのか?」という疑問です。
この疑問に答えるために必要なのが「確率」の知識。次回からは、統計学の心臓部とも言える「確率」の世界に入っていきます!
📚 次に読むべき記事
ヒストグラムの次は「確率」。統計学の心臓部に入っていきます。
ヒストグラムで最も重要な「正規分布」を詳しく解説。
ヒストグラムで見た「バラつき」を数値で表す方法を解説。

統計学のおすすめ書籍
統計学の「数式アレルギー」を治してくれた一冊
「Σ(シグマ)や ∫(インテグラル)を見ただけで眠くなる…」 そんな私を救ってくれたのが、小島寛之先生の『完全独習 統計学入門』です。
この本は、難しい記号を一切使いません。 「中学レベルの数学」と「日本語」だけで、検定や推定の本質を驚くほど分かりやすく解説してくれます。
「計算はソフトに任せるけど、統計の『こころ(意味)』だけはちゃんと理解したい」 そう願う学生やエンジニアにとって、これ以上の入門書はありません。
【QC2級】「どこが出るか」がひと目で分かる!最短合格へのバイブル
私がQC検定2級に合格した際、使い倒したのがこの一冊です。
この本の最大の特徴は、「各単元の平均配点(何点分出るか)」が明記されていること。 「ここは出るから集中」「ここは出ないから流す」という戦略が立てやすく、最短ルートで合格ラインを突破できます。
解説が分かりやすいため、私はさらに上の「QC1級」を受験する際にも、基礎の確認用として辞書代わりに使っていました。 迷ったらまずはこれを選んでおけば間違いありません。


