- 「二項分布」ってどんな分布?どういうときに使うの?
- 公式 P(X=k) = nCk × p^k × (1-p)^(n-k) の意味がわからない…
- 期待値がnp、分散がnp(1-p)になるのはなぜ?
- 「正規分布で近似できる」ってどういう条件?
- 二項分布の意味を「コイン投げ」で直感的に理解
- 確率の公式がなぜその形になるのか、一から導出
- 期待値np・分散np(1-p)の「なぜ」を完全解説
- 正規分布で近似できる条件と、連続修正の意味
「コインを10回投げて、表が何回出るか?」
「100個の製品を検査して、不良品は何個あるか?」
これらの問いに答えてくれるのが、二項分布です。
二項分布は統計学で最も重要な離散分布の一つで、品質管理、世論調査、医学研究、マーケティングなど、あらゆる分野で活用されています。
この記事では、公式を暗記するのではなく、「なぜその式になるのか」をコイン投げのイメージで徹底的に解説します。
目次
二項分布とは?一言でいうと
「成功」か「失敗」の2択をn回繰り返したとき、成功がk回起きる確率を表す分布
「二項」という名前は、結果が2種類(成功・失敗)しかないことに由来します。
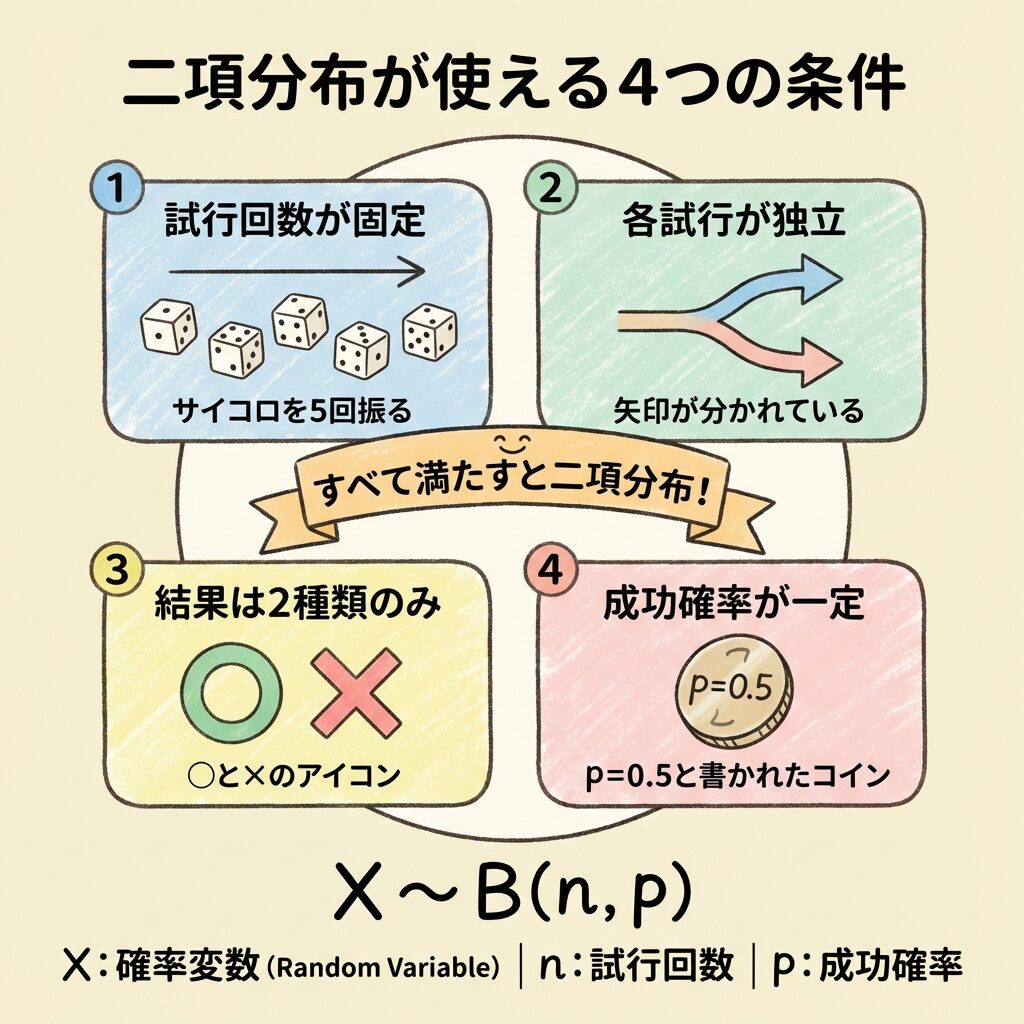
🎯 二項分布が使える4つの条件
二項分布は、以下の4つの条件をすべて満たす場合に使えます。
| 条件 | 説明 | コイン投げの例 |
|---|---|---|
| ① 試行回数が固定 | 何回繰り返すかが決まっている | 「10回投げる」と決めている |
| ② 各試行が独立 | 1回目の結果が2回目に影響しない | 1回目が表でも、2回目の確率は変わらない |
| ③ 結果は2種類のみ | 成功か失敗の2択 | 表(成功)か裏(失敗) |
| ④ 成功確率が一定 | 毎回同じ確率 | どの回も表が出る確率は50% |
「同じサイコロを何度も振る」「同じ条件で何度も抽選する」ような状況が二項分布です。毎回条件が変わってしまう場合は使えません。
📊 二項分布の記号
二項分布は B(n, p) と書きます。
| 記号 | 意味 | 例 |
|---|---|---|
| B | Binomial(二項)の頭文字 | − |
| n | 試行回数 | コインを10回投げる → n = 10 |
| p | 1回の試行での成功確率 | 表が出る確率 → p = 0.5 |
「コインを10回投げて表の回数を数える」なら、X 〜 B(10, 0.5) と書きます。
第7回:確率とは何か - 基本概念を理解する →
二項分布の確率公式を「導出」する
いよいよ本題です。二項分布の確率公式を、「なぜその式になるのか」を理解しながら導出しましょう。
🎯 具体例:コインを3回投げて、表が2回出る確率
まず、簡単な例で考えてみましょう。
【問題】
公正なコインを3回投げて、表がちょうど2回出る確率は?
Step 1:すべてのパターンを書き出す
3回投げて「表が2回」になるパターンは、何通りあるでしょうか?
| パターン | 1回目 | 2回目 | 3回目 | 表の回数 |
|---|---|---|---|---|
| ① | 表 | 表 | 裏 | 2回 |
| ② | 表 | 裏 | 表 | 2回 |
| ③ | 裏 | 表 | 表 | 2回 |
「表が2回」のパターンは3通りありますね。
Step 2:1パターンの確率を計算
例えば「表→表→裏」というパターンが起きる確率はいくつでしょう?
各回は独立なので、掛け算で計算できます。
「表→表→裏」の確率
= (表が出る確率)×(表が出る確率)×(裏が出る確率)
= 0.5 × 0.5 × 0.5 = 0.125
他の2パターン(「表→裏→表」「裏→表→表」)も同じく0.125です。
Step 3:全パターンを足す
「表が2回」になるのは、3つのパターンのいずれかが起きればいいので、足し算です。
P(表が2回) = 0.125 + 0.125 + 0.125 = 3 × 0.125 = 0.375
つまり、37.5%の確率で「表が2回」になります。
🔍 この計算を一般化する
今の計算を振り返ると、確率は次の2つの要素の掛け算で求められました。
| 要素 | 今回の例 | 一般化 |
|---|---|---|
| パターン数(何通りあるか) | 3通り | nCk |
| 1パターンの確率 | 0.5² × 0.5¹ | pk × (1-p)n-k |
📐 二項分布の確率公式(完成形)
以上をまとめると、二項分布の確率公式が導けます。
nCk:n回中k回成功するパターン数(組み合わせ)
pk:k回成功する確率
(1-p)n-k:(n-k)回失敗する確率
🧮 組み合わせ nCk の計算方法
「n回中k回を選ぶ」組み合わせの数は、次の公式で計算します。
例:3C2 の計算
「3回中2回を選ぶ」方法は3通り。先ほど書き出した「表表裏」「表裏表」「裏表表」の3パターンと一致しますね!
P(X = k) = 「k回成功するパターンが何通りあるか」×「そのパターンが起きる確率」
第8回:期待値 - 確率分布の中心を知る →

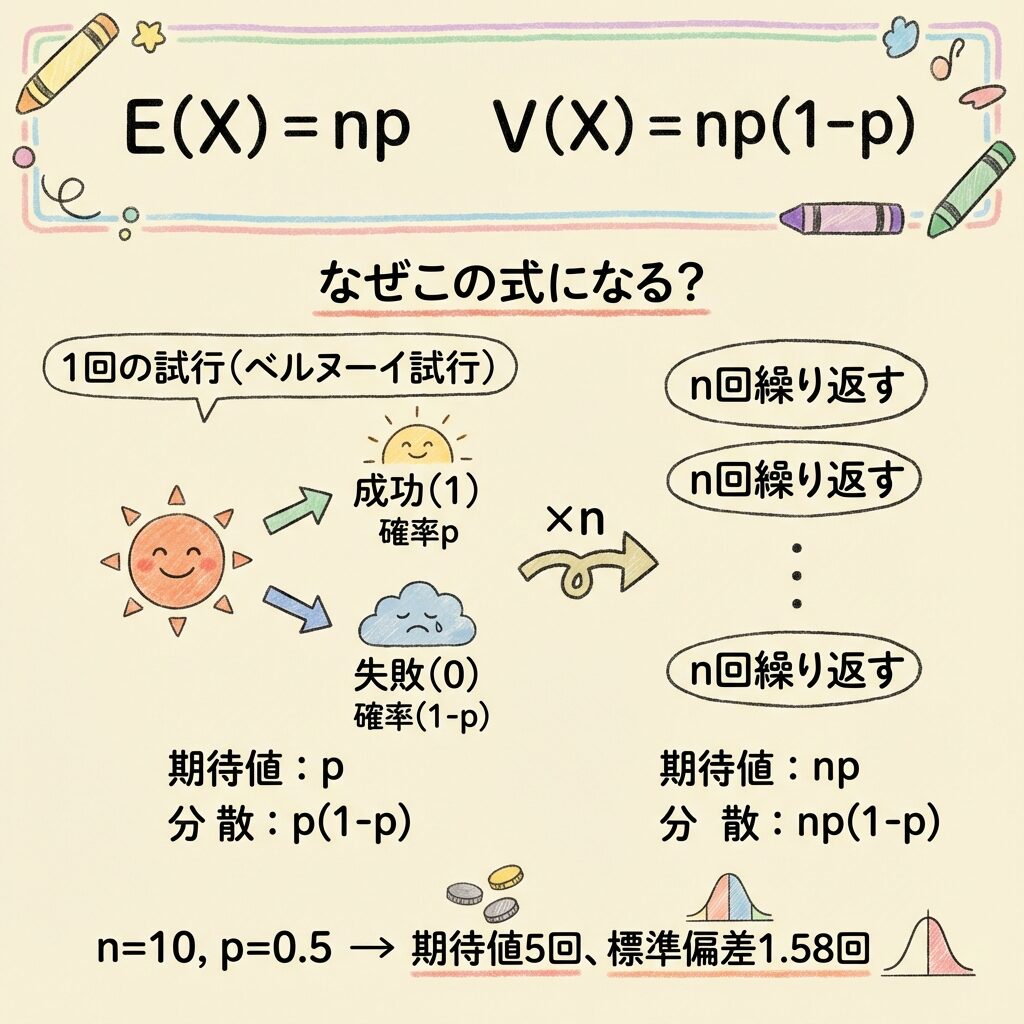
期待値 E(X) = np の導出
二項分布の期待値はE(X) = npという非常にシンプルな形になります。なぜこうなるのか、直感的に理解しましょう。
🎯 直感的な理解:「1回あたりの期待値」を足す
まず、1回だけコインを投げる場合を考えます。
1回投げたときの「表の期待回数」はpです(確率がそのまま期待値になる)。
これをn回繰り返すので、期待値は単純にn倍です。
E(X) = np
n:試行回数、p:成功確率
例:コインを10回投げる場合
n = 10、p = 0.5 のとき:
E(X) = 10 × 0.5 = 5回
「10回投げたら、平均して5回くらい表が出るだろう」という直感と一致しますね!
🔢 厳密な導出(数学的証明)
直感的な理解ができたところで、数学的にも確認しておきましょう。
【期待値の定義に従って計算】
E(X) = Σ k × P(X = k) (k = 0, 1, 2, ..., n)
ここで、二項分布は「n回のベルヌーイ試行の和」と考えられます。
X = X₁ + X₂ + ... + Xₙ (Xᵢは各回の結果、0か1)
期待値の加法性より:
E(X) = E(X₁) + E(X₂) + ... + E(Xₙ) = p + p + ... + p = np
分散 V(X) = np(1-p) の導出
分散も同じように、「1回あたりの分散」を足し上げることで導出できます。
🎯 直感的な理解:「1回あたりの分散」を足す
まず、1回だけコインを投げる場合の分散を計算します。
【1回投げの分散(ベルヌーイ分布)】
結果は「1(成功)」か「0(失敗)」
期待値:E(Xᵢ) = p
分散:V(Xᵢ) = E(Xᵢ²) - [E(Xᵢ)]²
= (1² × p + 0² × (1-p)) - p²
= p - p²
= p(1 - p)
各回の試行は独立なので、分散は足し算できます(分散の加法性)。
V(X) = np(1-p)
n:試行回数、p:成功確率、(1-p):失敗確率
例:コインを10回投げる場合
n = 10、p = 0.5 のとき:
V(X) = 10 × 0.5 × 0.5 = 2.5
標準偏差 = √2.5 ≈ 1.58回
10回投げると平均5回表が出て、±1.58回程度のばらつきが予想される。つまり「3〜7回くらいが普通」ということです。
🤔 なぜ分散は p(1-p) の形なのか?
分散の式 V = np(1-p) をよく見ると、p(1-p) という部分があります。これには深い意味があります。
p(1-p) の最大値はいつ?
p(1-p) は p = 0.5 のときに最大値 0.25 を取ります。
| p | 1-p | p(1-p) |
|---|---|---|
| 0.1 | 0.9 | 0.09 |
| 0.3 | 0.7 | 0.21 |
| 0.5 | 0.5 | 0.25(最大) |
| 0.7 | 0.3 | 0.21 |
| 0.9 | 0.1 | 0.09 |
成功確率が50%のとき、結果が最も「読めない」ので、ばらつき(分散)が最大になります。
逆に、p = 0.01(ほぼ失敗)や p = 0.99(ほぼ成功)のときは、結果がほぼ決まっているので、ばらつきは小さくなります。
二項分布の「形」はどう変わる?
二項分布のグラフの形は、成功確率pと試行回数nによって大きく変わります。
📊 成功確率pによる形の変化
| pの値 | 分布の形 | イメージ |
|---|---|---|
| p = 0.5 | 左右対称な山型 | きれいな釣鐘型。中央が最も高い。 |
| p < 0.5 (例:p = 0.2) |
右に歪んだ形 | 成功が少ない(左側)に偏る。右に長い尾。 |
| p > 0.5 (例:p = 0.8) |
左に歪んだ形 | 成功が多い(右側)に偏る。左に長い尾。 |
pが0.5から離れるほど、分布は「偏る」。成功しにくい(p小)なら成功0〜1回に集中し、成功しやすい(p大)なら成功n回近くに集中します。
📊 試行回数nによる形の変化
| nの値 | 分布の形 | イメージ |
|---|---|---|
| nが小さい (例:n = 5) |
階段状・ガタガタ | 棒グラフが数本だけ。離散的な印象。 |
| nが大きい (例:n = 100) |
なめらかな山型 | 棒グラフが密集して、正規分布に近い曲線に。 |
nが大きくなると、二項分布は正規分布に近づく。これが後で学ぶ「正規近似」の根拠です。
具体例で計算してみよう
📋 例題1:コイン投げ(n=5, p=0.5)
【問題】
公正なコインを5回投げて、表がちょうど3回出る確率は?
Step 1:必要な値を確認
- n = 5(5回投げる)
- k = 3(表が3回)
- p = 0.5(表が出る確率)
- 1 - p = 0.5(裏が出る確率)
Step 2:組み合わせ 5C3 を計算
Step 3:確率を計算
P(X = 3) = 5C3 × p³ × (1-p)²
= 10 × (0.5)³ × (0.5)²
= 10 × 0.125 × 0.25
= 10 × 0.03125
P(X = 3) = 0.3125 = 31.25%
📋 例題2:品質検査(n=50, p=0.03)
【問題】
不良率3%の製品を50個検査して、不良品が0個である確率は?
Step 1:必要な値を確認
- n = 50(50個検査)
- k = 0(不良品0個)
- p = 0.03(不良率3%)
- 1 - p = 0.97(良品率97%)
Step 2:計算
P(X = 0) = 50C0 × (0.03)⁰ × (0.97)⁵⁰
= 1 × 1 × (0.97)⁵⁰
= (0.97)⁵⁰
≈ 0.218
P(X = 0) ≈ 0.218 = 21.8%
約22%の確率で「不良品ゼロ」になる
この計算を逆に使うと、「不良品がX個以上出たら異常」という管理限界を設定できます。これが抜取検査の基礎です。
二項分布を正規分布で近似する
二項分布の計算は、nが大きくなると非常に面倒になります。たとえば100C47を手計算するのは大変ですよね。
しかし、ある条件を満たせば、二項分布を正規分布で近似できます。これにより計算が劇的に簡単になります。
🤔 なぜ正規分布で近似できるのか?
これは中心極限定理という統計学の最も重要な定理によります。
同じ分布に従う独立な確率変数をたくさん足し合わせると、その和は正規分布に近づく。
二項分布は、「n回のベルヌーイ試行の和」でしたよね。
つまり、nが十分大きければ、中心極限定理により正規分布に近づくのです。
✅ 正規近似が使える条件
どんなときでも近似できるわけではありません。以下の条件を満たす必要があります。
np ≥ 5 かつ n(1-p) ≥ 5
(より厳密には np ≥ 10 かつ n(1-p) ≥ 10 を使うこともある)
この条件の意味
| 条件 | 意味 |
|---|---|
| np ≥ 5 | 「成功」の期待回数が5回以上 |
| n(1-p) ≥ 5 | 「失敗」の期待回数が5回以上 |
成功も失敗も「ある程度の回数が期待できる」状態でないと、正規分布の釣鐘型にならないのです。
たとえば p = 0.01, n = 10 だと np = 0.1 となり、ほとんど成功しない極端な分布になります。これを正規分布で近似するのは無理があります。
条件を満たすかチェックする例
| 設定 | np | n(1-p) | 近似OK? |
|---|---|---|---|
| n=100, p=0.3 | 30 | 70 | ✅ OK |
| n=50, p=0.5 | 25 | 25 | ✅ OK |
| n=20, p=0.1 | 2 | 18 | ❌ NG(np < 5) |
| n=10, p=0.5 | 5 | 5 | △ ギリギリ |
📐 正規近似の公式
条件を満たせば、二項分布 B(n, p) は次の正規分布で近似できます。
X 〜 B(n, p) → X ≈ N(np, np(1-p))
平均:μ = np
分散:σ² = np(1-p)
つまり、二項分布の期待値と分散を、そのまま正規分布のパラメータとして使うだけです。

連続修正(Yatesの修正)とは?(QC検定1級レベル)
正規近似を使うとき、連続修正を行うと精度が上がります。
🤔 なぜ連続修正が必要なのか?
二項分布は離散分布(0, 1, 2, 3, ...の整数値のみ)ですが、正規分布は連続分布(どんな実数も取れる)です。
この「離散→連続」の変換でズレが生じるため、±0.5の補正を行います。
P(X = k) → P(k − 0.5 < Y < k + 0.5)
P(X ≤ k) → P(Y < k + 0.5)
P(X ≥ k) → P(Y > k − 0.5)
※ Y は近似した正規分布に従う確率変数
離散値「30」は、連続値では「29.5〜30.5」の区間に対応すると考えます。
階段の1段を、坂道の一定区間に置き換えるイメージです。
🧮 正規近似の計算例(連続修正あり)
【問題】
ある製品の不良率は5%である。1000個検査したとき、不良品が40個以下である確率を求めよ。
Step 1:正規近似の条件を確認
- n = 1000, p = 0.05
- np = 1000 × 0.05 = 50 ≥ 5 ✅
- n(1-p) = 1000 × 0.95 = 950 ≥ 5 ✅
条件を満たすので、正規近似が使えます。
Step 2:正規分布のパラメータを計算
- 平均:μ = np = 1000 × 0.05 = 50
- 分散:σ² = np(1-p) = 1000 × 0.05 × 0.95 = 47.5
- 標準偏差:σ = √47.5 ≈ 6.89
X 〜 B(1000, 0.05) ≈ N(50, 47.5)
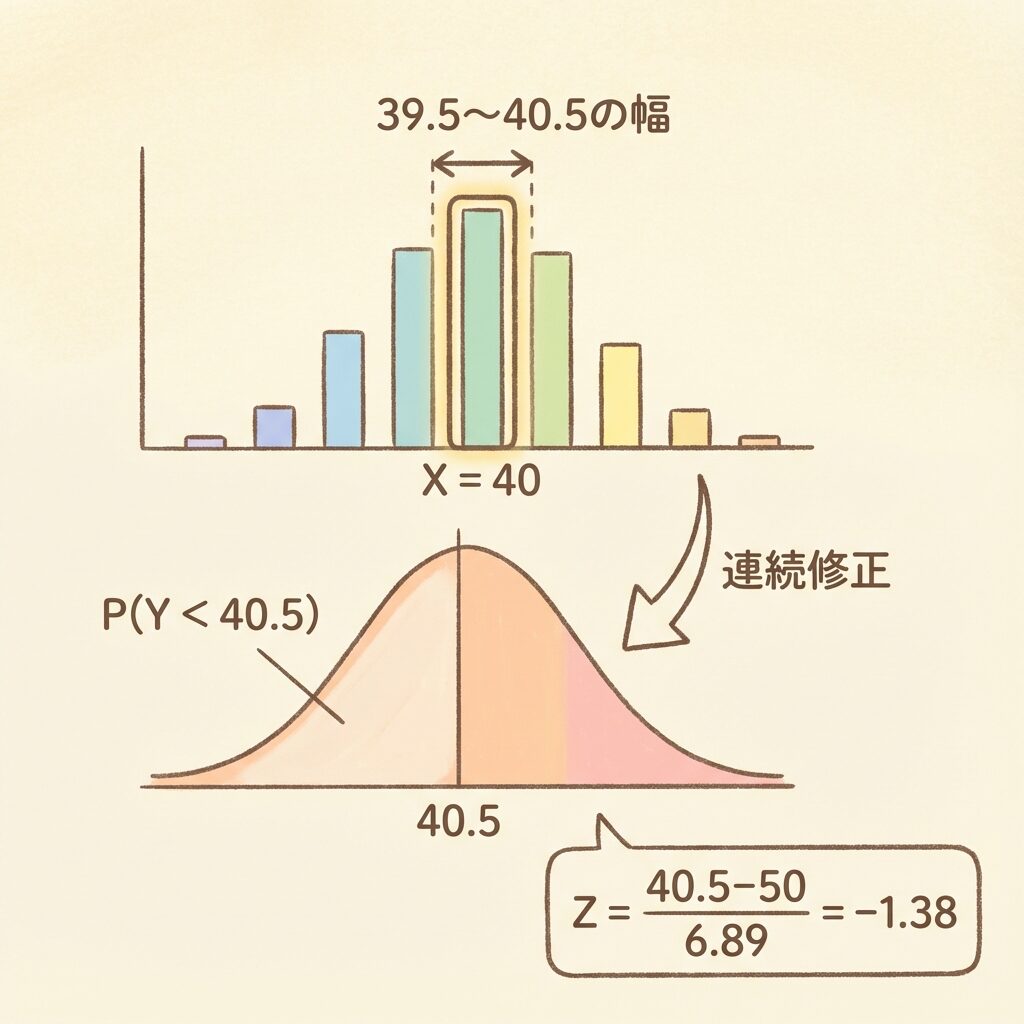
Step 3:連続修正を適用
P(X ≤ 40) を求めたいので、連続修正により:
P(X ≤ 40) ≈ P(Y < 40.5) (0.5を足す)
Step 4:標準化してZ値を計算
Step 5:標準正規分布表から確率を読む
P(Z < −1.38) ≈ 0.0838
P(X ≤ 40) ≈ 0.084 = 8.4%
1000個検査して不良品が40個以下になる確率は約8.4%
連続修正なしで計算すると:
Z = (40 − 50) / 6.89 = −1.45
P(Z < −1.45) ≈ 0.0735 = 7.4%
約1%の差が生じます。試験では連続修正が指定されることがあるので、問題文をよく確認しましょう。
まとめ:二項分布の全体像
- 二項分布 B(n, p):「成功・失敗」をn回繰り返し、成功回数の確率を表す分布
- 4つの条件:① 固定回数、② 独立、③ 2択、④ 成功確率一定
- 確率公式:P(X=k) = nCk × pk × (1-p)n-k
- 期待値:E(X) = np(「1回あたりの期待値」×「回数」)
- 分散:V(X) = np(1-p)(p=0.5で最大)
- 正規近似の条件:np ≥ 5 かつ n(1-p) ≥ 5
- 連続修正:離散→連続の変換で ±0.5 の補正を行う
キーワード解説一覧
| 用語 | 意味・ポイント |
|---|---|
| 二項分布 B(n, p) |
成功確率pの試行をn回繰り返したとき、成功回数Xが従う確率分布。Binomial Distributionの略。 |
| ベルヌーイ試行 | 結果が「成功」か「失敗」の2通りしかない試行。各回が独立で、成功確率が一定。 |
| ベルヌーイ分布 | n=1の二項分布。1回の試行の結果(0か1)が従う分布。期待値p、分散p(1-p)。 |
| 組み合わせ nCk |
n個からk個を選ぶ方法の数。n!/(k!(n-k)!)で計算。順序は考慮しない。 |
| 正規近似 | nが大きいとき、二項分布をN(np, np(1-p))で近似すること。np≥5, n(1-p)≥5が条件。 |
| 連続修正 (Yatesの修正) |
離散分布を連続分布で近似するとき、±0.5の補正を行うこと。近似精度が向上する。 |
| 中心極限定理 | 独立な確率変数の和が、十分な数を足し合わせると正規分布に近づくという定理。正規近似の根拠。 |
| 離散分布 | 確率変数が0, 1, 2, ...のような飛び飛びの値を取る分布。二項分布、ポアソン分布など。 |
試験で問われるポイント
パターン1:確率の計算
「n回中k回成功する確率を求めよ」→ 公式に代入して計算
パターン2:期待値・分散の計算
「期待値と標準偏差を求めよ」→ E(X)=np, V(X)=np(1-p)
パターン3:正規近似の条件判定
「正規近似が適用できるか判定せよ」→ np≥5 かつ n(1-p)≥5 を確認
パターン4:正規近似による確率計算
「P(X≤k)を正規近似で求めよ」→ 連続修正してZ値を計算
📚 次に読むべき記事
二項分布でnが大きくpが小さいとき、ポアソン分布で近似できます。事故件数や来客数の分析に使われる重要な分布です。
正規近似の「近似先」である正規分布を詳しく学びましょう。統計学で最も重要な連続分布です。
二項分布は抜取検査の基礎です。「何個中何個不良だったらNG?」を決める方法を学びましょう。
統計学を体系的に学びたい方はこちら。全体像から詳細まで網羅しています。
