- 指数分布の公式「e−λt」が出てきたけど、なぜこの式なのかわからない
- MTBFと故障率λの関係がごちゃごちゃして混乱する
- 「無記憶性」って何?なぜそんな性質があるの?
- QC検定や信頼性工学の問題が解けない…
- 指数分布とは何か?を日常の例でイメージ理解
- なぜ e−λt という式になるのかを図解で徹底解説
- 3つの公式の意味と使い分け
- 「無記憶性」の直感的な理解
- 具体的な計算例で完全マスター
「電球って、いつ切れるんだろう?」
「このスマホ、あと何年使えるかな?」
こんな疑問、日常でよく感じますよね。実は、こうした「いつ起きるかわからないこと」を数学で表現できる道具があるんです。
それが「指数分布」です。
指数分布は、信頼性工学やQC検定で必ず登場する超重要な分布です。でも、「e−λt」という式を見ると、「なぜこんな式になるの?」と疑問に思う方も多いはず。
この記事では、公式の「なぜ?」を徹底的に図解します。読み終わる頃には、指数分布が「当たり前」に感じられるようになりますよ。
目次
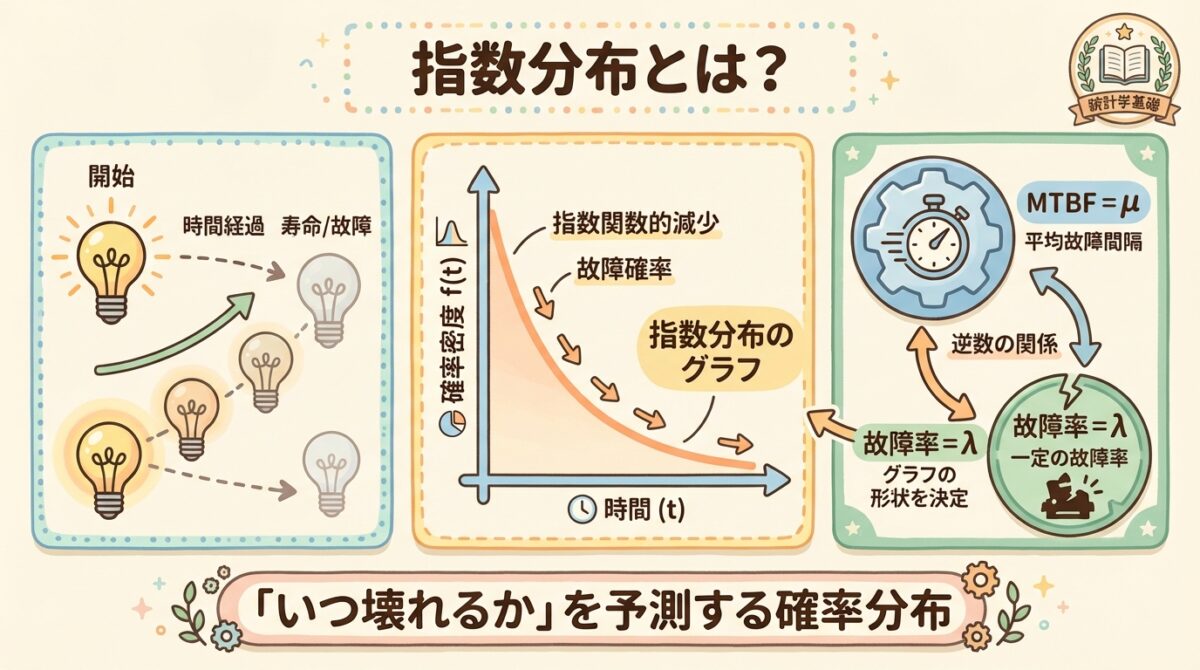
🌟 指数分布とは?|「次に起きるまでの時間」を表す分布
💡 指数分布が登場する場面
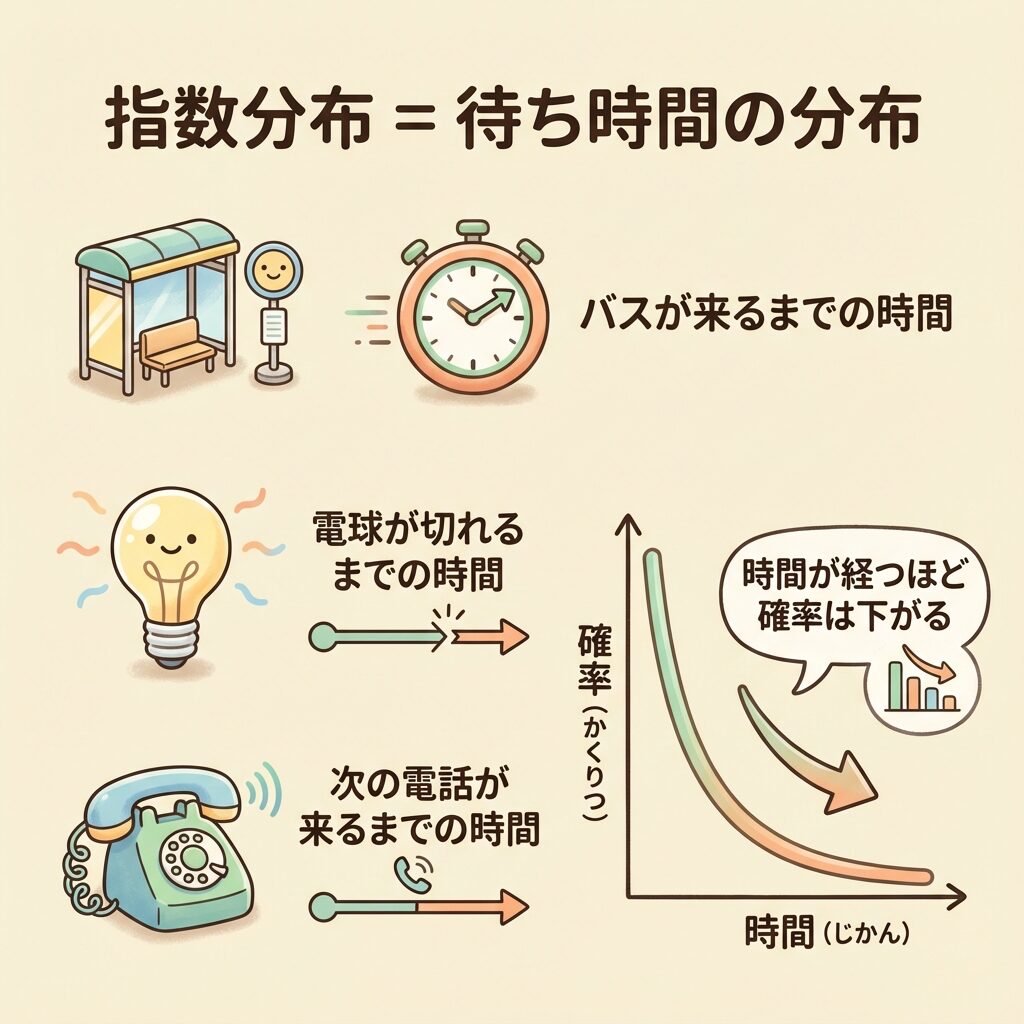
指数分布は、「次に何かが起きるまでの時間」を表す確率分布です。
身近な例を挙げると:
| 場面 | 指数分布で表せること |
|---|---|
| 💡 電球 | 電球が切れるまでの時間 |
| 📱 スマホ | スマホが故障するまでの時間 |
| 🚌 バス停 | 次のバスが来るまでの待ち時間 |
| 📞 コールセンター | 次の電話がかかってくるまでの時間 |
| 🏭 工場の機械 | 機械が故障するまでの稼働時間 |
共通点は、「いつ起きるかはランダムだけど、平均的な間隔は分かっている」という状況です。
📊 指数分布のグラフの形
指数分布のグラフは、右肩下がりの曲線です。
・時間0のところが一番高い(すぐに起きる可能性が一番高い)
・時間が経つほど、確率は下がっていく
・でも、いつまでもゼロにはならない(長く待つこともあり得る)
例えば、平均5分間隔でバスが来る場合、「すぐ来る(1分以内)」可能性が一番高く、「10分以上待つ」可能性は低いけどゼロではない、というイメージです。
🤔 なぜ e−λt なのか?|公式の意味を徹底解説
指数分布の公式で「e−λt」が出てくると、「なぜ e なの?」「なぜマイナスなの?」と疑問に思いますよね。
この章では、公式がなぜこの形になるのかを、中学生でもわかるように説明します。
💰 複利計算の「逆バージョン」で理解する
まず、e(ネイピア数)がどこから来るか、身近な例で説明します。
📈 複利計算:お金が「増える」場合
銀行に100万円を預けると、利息がついて増えていきますよね。これが複利計算です。
| 年数 | 年利10%の場合 | 計算式 |
|---|---|---|
| 0年 | 100万円 | 100 × 1.10 |
| 1年 | 110万円 | 100 × 1.11 |
| 2年 | 121万円 | 100 × 1.12 |
| 3年 | 133万円 | 100 × 1.13 |
複利計算では、「今あるものの一定割合が増えていく」という仕組みです。
📉 指数分布:生存率が「減る」場合
指数分布は、これの逆バージョンです。「今生きているものの一定割合が減っていく」という仕組みです。
| 時刻 | 生存率(毎回10%減) | イメージ |
|---|---|---|
| 0 | 100% | 全員元気 |
| 1 | 90% | 100 × 0.9 = 90 |
| 2 | 81% | 90 × 0.9 = 81 |
| 3 | 72.9% | 81 × 0.9 = 72.9 |
「残っているものの一定割合が毎瞬間減っていく」
これを連続的に(無限に細かく)考えると、数式で e−λt になる!
🔢 公式の導出を図で理解する
もう少し詳しく説明しましょう。
いま、故障率λ(ラムダ)という数値があるとします。これは「単位時間あたりに、どのくらいの割合で故障するか」を表します。
例:λ = 0.1/年
→ 「1年間で、生き残っているものの10%が故障する」という意味
λが大きいほど、壊れやすい(寿命が短い)
λが小さいほど、壊れにくい(寿命が長い)
時刻tまで生き残る確率 R(t) は、次のように考えます:
| 考え方 | 数式 |
|---|---|
| 時刻0では全員生きている | R(0) = 1(100%) |
| 微小時間Δtの間に、生存者の λΔt 割合が故障 | R(t+Δt) = R(t) × (1 − λΔt) |
| これを無限に繰り返すと… | R(t) = e−λt |
時刻tまで「生き残っている」確率
つまり、e−λtは「毎瞬間、一定割合で故障するリスクがあるとき、時刻tまで生き残る確率」を表しているんです。

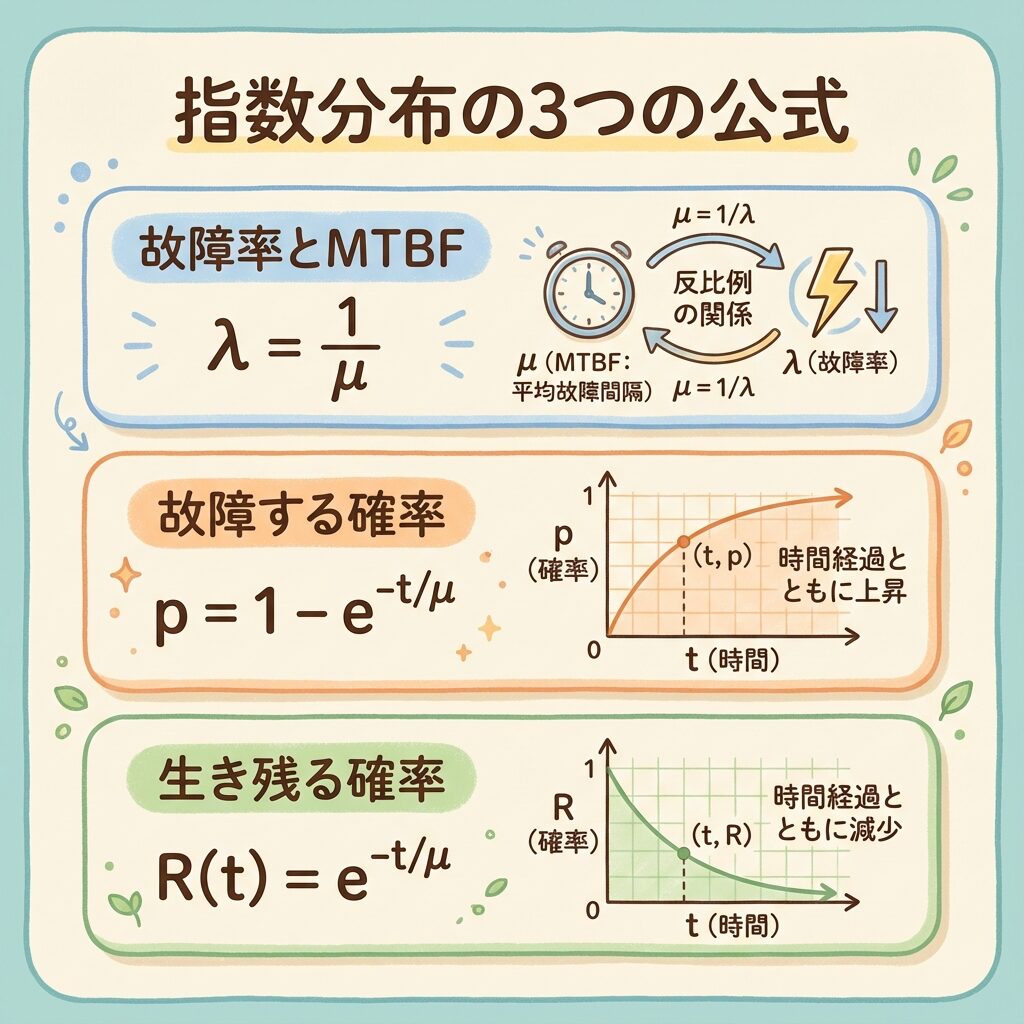
📐 指数分布の3つの公式|これだけ覚えればOK!
指数分布で覚えるべき公式は3つだけです。それぞれの意味を丁寧に解説します。
🔗 公式① 故障率λとMTBFμの関係
λ(ラムダ)は故障率、μ(ミュー)はMTBF(平均故障間隔)です。この2つは逆数の関係にあります。
| 記号 | 名前 | 意味 | 例 |
|---|---|---|---|
| λ | 故障率 | 単位時間あたりの故障しやすさ | λ = 0.1/年(10%/年) |
| μ | MTBF | 平均で何時間もつか | μ = 10年 |
λ(故障率)が大きい → よく壊れる → MTBF(寿命)が短い
λ(故障率)が小さい → 壊れにくい → MTBF(寿命)が長い
反比例の関係なので、λ = 1/μ です!
📊 公式② 時刻tまでに故障する確率(累積分布関数)
時刻tまでに「故障している」確率
これは「時刻tまでに壊れている確率」です。1 − R(t) の関係になっています。
✨ 公式③ 時刻tまで生き残る確率(信頼度関数)
時刻tまで「生き残っている」確率
これが一番よく使う式です。「まだ壊れていない確率」=「信頼度」を表します。
📋 3つの公式の関係をまとめると
| 公式 | 式 | 意味 |
|---|---|---|
| ①基本関係 | λ = 1/μ | 故障率とMTBFは逆数 |
| ②故障確率 | F(t) = 1 − e−t/μ | 時刻tまでに壊れている確率 |
| ③生存確率 | R(t) = e−t/μ | 時刻tまで生き残る確率 |
故障確率と生存確率を足すと必ず1(100%)になります。
「壊れている」か「生き残っている」かのどちらかだからです。
🧠 無記憶性とは?|指数分布の不思議な性質
指数分布には、「無記憶性」という不思議な性質があります。これを理解すると、指数分布の本質がわかります。
🤔 無記憶性って何?
無記憶性とは、「過去の経過時間が、将来の故障確率に影響しない」という性質です。
言葉だけだと難しいので、具体例で説明します。
友人A:「俺のスマホ、もう2年使ってるから、そろそろ壊れそう」
友人B:「私のスマホ、まだ買ったばかりだから安心」
指数分布では:
2年使ったスマホも、買ったばかりのスマホも、
「明日壊れる確率」は同じ!
「えっ、それっておかしくない?」と思いますよね。でも、これが指数分布の特徴なんです。
📐 数式で確認してみよう
無記憶性を数式で表すと、こうなります:
「すでにs時間経過した条件で、さらにt時間もつ確率」=「最初からt時間もつ確率」
実際に計算して確認してみましょう:
| ステップ | 計算 |
|---|---|
| 条件付き確率の定義 | P(T > s+t | T > s) = P(T > s+t) / P(T > s) |
| 指数分布の式を代入 | = e−λ(s+t) / e−λs |
| 指数法則で計算 | = e−λs−λt / e−λs = e−λt |
| 結果 | = P(T > t) ← 最初からt時間もつ確率と同じ! |
🎯 無記憶性が成り立つ理由
無記憶性が成り立つのは、「故障率λが常に一定」という前提があるからです。
毎日サイコロを振って「1が出たら故障」というゲームを考えてください。
・昨日まで100日連続で1が出なかった
・だからといって、今日1が出る確率は変わらない(1/6のまま)
指数分布はこれと同じ考え方です。過去は過去、今日は今日。
⚠️ 現実では無記憶性が成り立たないことも
現実の製品は、使い続けると劣化して故障しやすくなります。つまり、故障率λが時間とともに変化します。
| 期間 | 故障率λ | 使う分布 |
|---|---|---|
| 初期故障期 | 時間とともに減少 | ワイブル分布(m < 1) |
| 偶発故障期 | 一定(λ = const) | 指数分布 ← ここで使う! |
| 摩耗故障期 | 時間とともに増加 | ワイブル分布(m > 1) |
指数分布は、故障率が一定の「偶発故障期」で使う分布です。初期故障期や摩耗故障期には、ワイブル分布を使います。
🧮 具体例で計算してみよう
📱 例題1:スマホの寿命予測
あるスマホの平均寿命(MTBF)は3年です。
2年後もまだ使える確率は何%でしょうか?
| ステップ | 計算 |
|---|---|
| ① 条件の確認 | μ = 3年、t = 2年 |
| ② 公式に代入 | R(2) = e−2/3 = e−0.667 |
| ③ 計算 | = 0.513 |
| 答え | 約51%(半分くらいはまだ使える) |
💡 例題2:電球の故障確率
ある電球のMTBFは1000時間です。
500時間使ったとき、すでに切れている確率は何%でしょうか?
| ステップ | 計算 |
|---|---|
| ① 条件の確認 | μ = 1000時間、t = 500時間 |
| ② 故障確率の公式 | F(500) = 1 − e−500/1000 = 1 − e−0.5 |
| ③ 計算 | = 1 − 0.607 = 0.393 |
| 答え | 約39%(4割近くは切れている) |
・e−0.5 ≈ 0.61(約60%生存)
・e−1 ≈ 0.37(約37%生存)← MTBFと同じ時間が経過
・e−2 ≈ 0.14(約14%生存)
・e−3 ≈ 0.05(約5%生存)

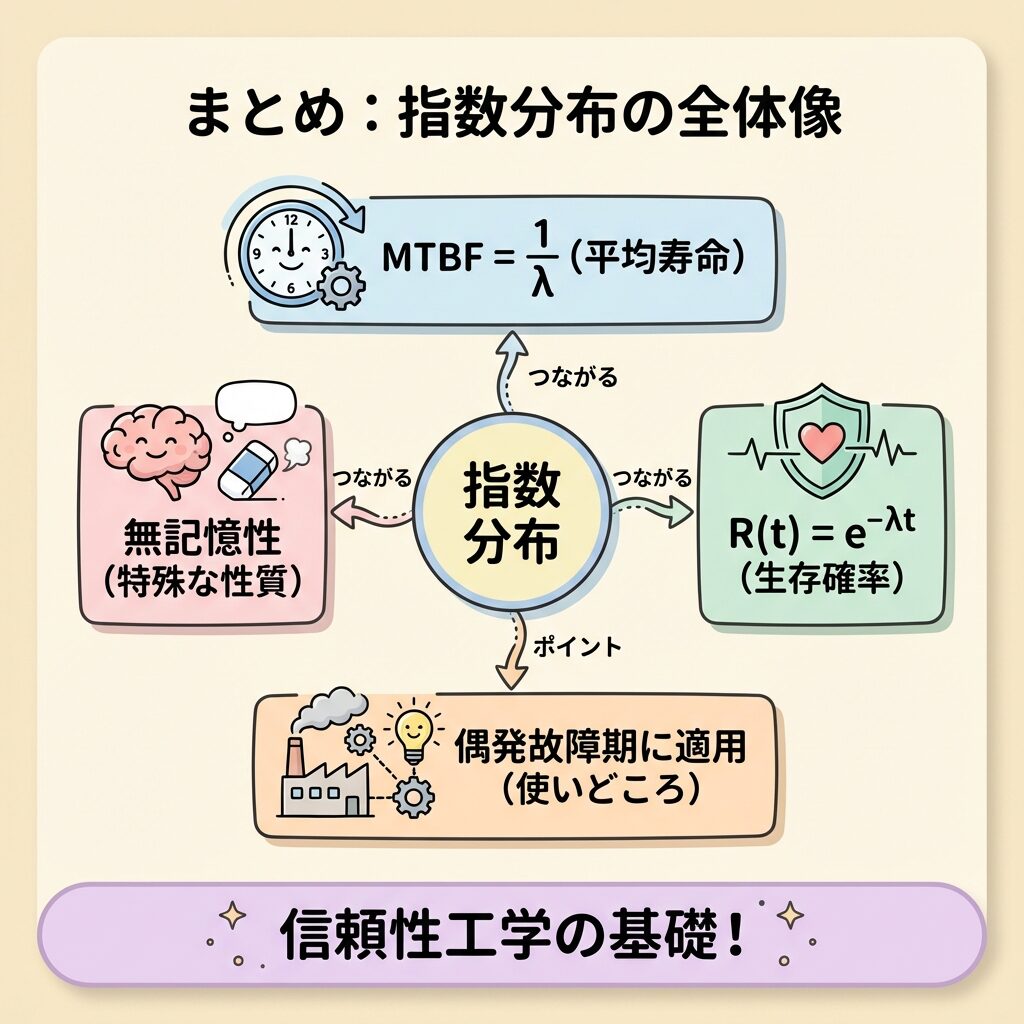
📝 まとめ|指数分布の全体像
この記事では、指数分布の基本から公式の意味、無記憶性まで解説しました。
1. 指数分布とは?
→ 「次に何かが起きるまでの時間」を表す確率分布
2. なぜ e−λt なのか?
→ 「残りの一定割合が毎瞬間減る」を連続的に考えた結果
3. 3つの公式
→ λ = 1/μ、F(t) = 1−e−t/μ、R(t) = e−t/μ
4. 無記憶性
→ 過去の経過時間が将来の故障確率に影響しない(故障率が一定だから)
5. 使いどころ
→ 故障率が一定の「偶発故障期」で使う
| 故障率とMTBF | λ = 1/μ |
| 生存確率(信頼度) | R(t) = e−t/μ |
| 故障確率 | F(t) = 1 − e−t/μ |
指数分布は、信頼性工学やQC検定で必ず登場する重要な分布です。公式を暗記するだけでなく、「なぜその式になるのか」を理解しておくと、応用問題にも対応できるようになります。
📚 次に読むべき記事
指数分布と組み合わせて使う「離散型」の分布を学ぶ
指数分布と表裏一体の関係にある「ポアソン分布」を学ぶ
指数分布の実務での活用場面を理解する