📌 この記事の位置づけ
「実験計画法の基礎概念シリーズ」第6回。前回は「実験の3原則」を学びました。今回は混同しやすい「繰り返し」と「反復」の違いをスッキリ解説します。
「繰り返しと反復って、同じ意味じゃないの?」
「どっちも"何回かやる"ってことでしょ?」
実は、この2つは明確に違います。
この違いを知らないと、誤差の見積もりを間違えるという致命的なミスにつながります。
目次
結論:連続か、ランダムか
まず結論をお伝えします。
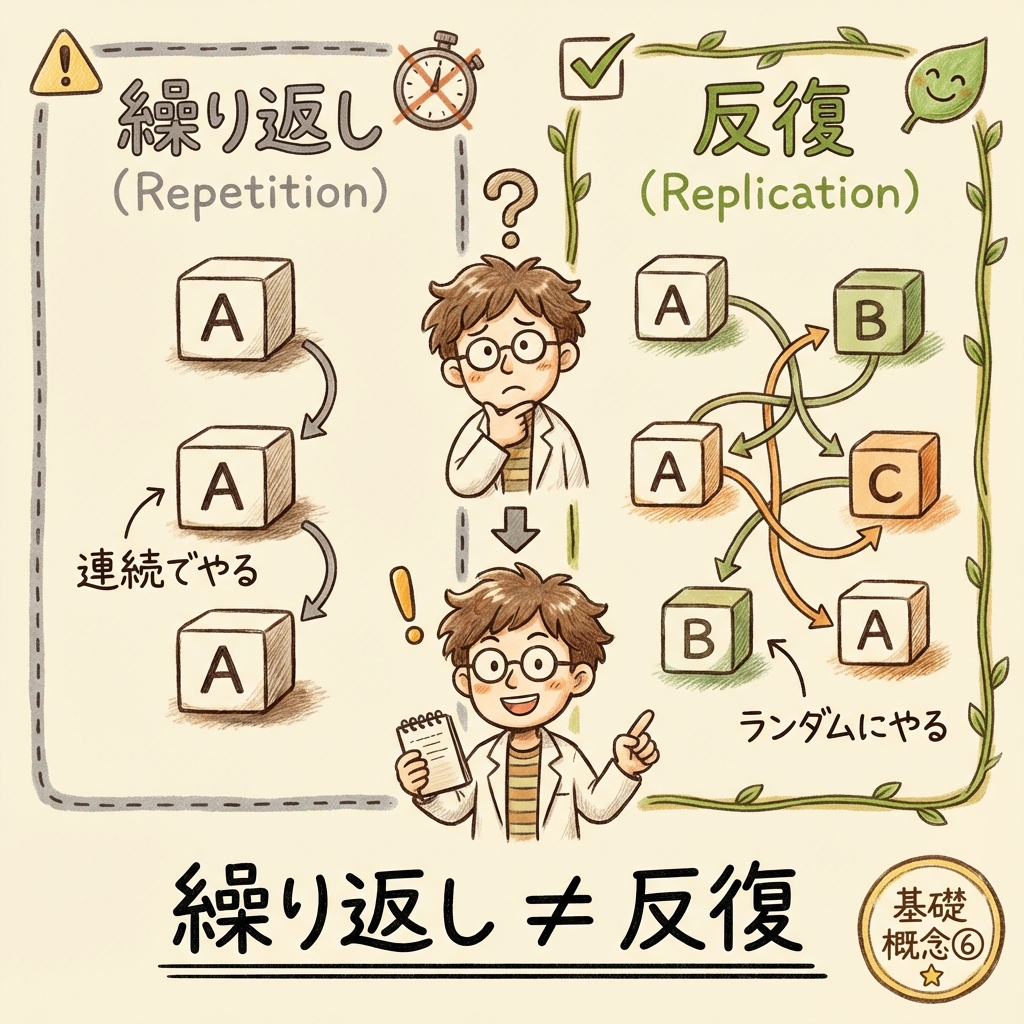
繰り返し(Repetition)
同じ条件を連続で複数回やる
A → A → A
(まとめてやる)
反復(Replication)
同じ条件をランダムに複数回やる
A → B → A → C → A
(バラバラにやる)
どちらも「同じ条件で複数回やる」点は同じですが、実験の順序が違うのです。
繰り返し(Repetition)とは?
📋 繰り返しの定義
繰り返しとは、同じ条件の実験を連続して行うことです。
条件を変えずに、続けて何度も測定すること。
英語では「Repetition(レペティション)」。
🧪 具体例:繰り返しのやり方
3つの条件(A、B、C)を各3回ずつテストする場合:
繰り返しの実験順序
A A A → B B B → C C C
「Aを3回連続」→「Bを3回連続」→「Cを3回連続」という流れです。
反復(Replication)とは?
📋 反復の定義
反復とは、同じ条件の実験をランダムな順序で行うことです。
条件の順序をシャッフルして複数回測定すること。
英語では「Replication(レプリケーション)」。
🧪 具体例:反復のやり方
同じ3条件を各3回ずつ、今度は反復でやる場合:
反復の実験順序(ランダム)
B A C C A B B C A
順番がバラバラになっていますね。これが反復です。
なぜ「反復」が重要なのか?
「どっちでも同じ結果じゃないの?」と思うかもしれません。
でも、繰り返しには落とし穴があるのです。
⚠️ 繰り返しの問題点
繰り返し(連続実施)の場合、こんな問題が起こります。
❌ 繰り返しで起こる問題
- 条件Aは朝に3回(室温20℃)
- 条件Bは昼に3回(室温25℃)
- 条件Cは夕方に3回(室温22℃)
→ 条件の効果なのか、時間帯(室温)の影響なのか区別できない!
連続でやると、特定の条件だけに環境変化の影響が偏るのです。
これでは、誤差を正しく見積もれません。
✅ 反復ならこの問題を解決できる
⭕ 反復(ランダム実施)なら…
- 朝に A、B、C がランダムに実施される
- 昼にも A、B、C がランダムに実施される
- 夕方にも A、B、C がランダムに実施される
→ 時間帯の影響がすべての条件に均等に散らばる!
これが、前回学んだ「ランダム化」の原則と結びつくわけです。
比較表で整理
| 項目 | 繰り返し | 反復 |
|---|---|---|
| 英語 | Repetition | Replication |
| 実験順序 | 連続(まとめて) | ランダム(バラバラ) |
| イメージ | A→A→A→B→B→B | B→A→C→A→B→C |
| 環境変化の影響 | 偏る 😟 | 均等に散らばる 😊 |
| 誤差の見積もり | 過小評価しがち | 正しく評価できる |
実験計画法では、基本的に「反復」を使うのが正解です。
まとめ
📌 この記事のポイント
- 繰り返し=同じ条件を連続で複数回やる
- 反復=同じ条件をランダムな順序で複数回やる
- 繰り返しだと、環境変化の影響が特定の条件に偏る
- 反復なら、影響が均等に散らばるので誤差を正しく評価できる
- 実験計画法では反復が基本!
次の記事では、「主効果」について解説します。因子を変えると結果がどれだけ変わるのか?を数値で表す方法を学びましょう。
関連記事【あなたの悩みを解決】
🤔「繰り返し回数の目安を知りたい」
→ 繰り返しとは?同じ条件で複数回実験する理由|基礎概念④🤔「ランダム化の原則をもう一度確認したい」
→ 実験の3原則|ランダム化・反復・局所管理を図解|基礎概念⑤🤔「誤差を正しく見積もる方法を知りたい」
→ 誤差とは?実験で避けられないバラつきの正体|基礎概念⑩🤔「有効繰返し数の計算方法を知りたい」
→ 有効繰返し数の「2つの計算式」を完全マスター🤔「分散分析で誤差をどう扱うか知りたい」
→ 群間平方和と群内平方和の分解|データを「効果」と「誤差」に切り分ける🤔「実験計画法の全体像を把握したい」
→ 【完全版】実験計画法の学習マップ|基礎から応用まで体系的に学ぶ🤔「QC検定対策として学びたい」
→ 【合格体験記】知識ゼロから半年でQC検定2級に合格した勉強法🤔「直交表の使い方を知りたい」
→ 【完全図解】L4直交表・L8直交表の使い方|割り付けの全手順