目次
⚡ こんな悩みを解決します
- ✅ 充放電の指数関数の式が難しくて理解できない
- ✅ 時定数τ(タウ)って結局何なの?
- ✅ 63.2%、86.5%って数字をどう使えばいいの?
- ✅ 充電曲線と放電曲線がごちゃごちゃになる
📖 この記事を読むとわかること
- 時定数τ = RCの物理的な意味(水タンクのイメージで理解)
- 充電曲線・放電曲線のグラフの見方と特徴
- 試験で使える「63.2%」「86.5%」の暗記ルール
- 指数関数を使わない簡単な計算方法
- 過渡現象の問題の解き方パターン
電気はイメージが全て!この記事では、複雑な数式より「何が起きているか」を視覚的に理解することを最優先にします。一緒に学んでいきましょう!💡
🔋 コンデンサの充放電とは?
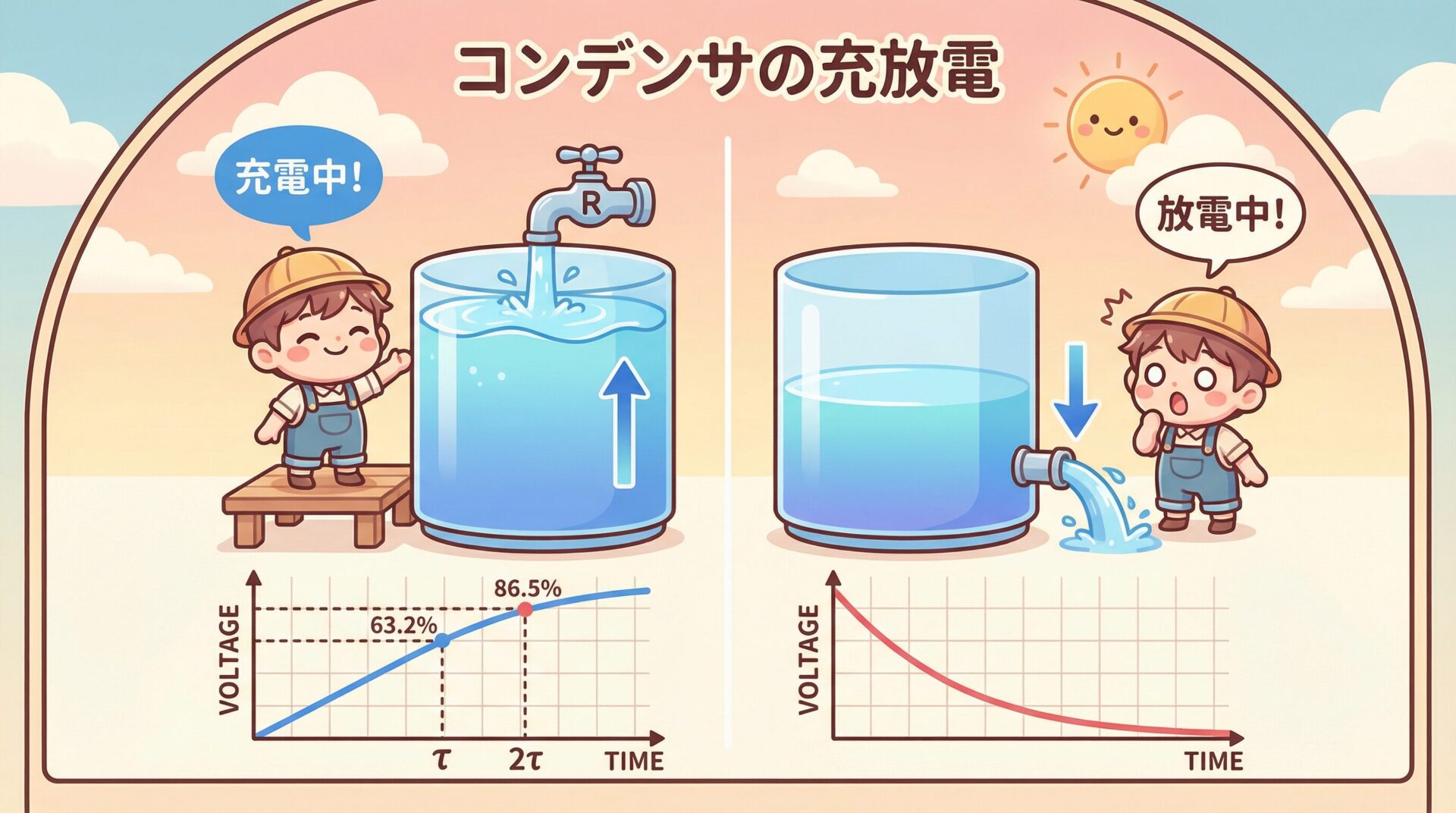
💧 水タンクで理解する充放電
コンデンサの充放電を理解する最良の方法は、水タンクのイメージを使うことです。電気の流れは目に見えませんが、水の流れならイメージできますよね!
💡 水タンクの比喩
🪣 コンデンサC = バケツ(容器)
大きなバケツほど、たくさん水を溜められる = 大きなCほど、たくさん電荷を蓄えられる
🚰 抵抗R = 蛇口の細さ
細い蛇口(大きなR)= ゆっくり水が流れる
太い蛇口(小さなR)= 速く水が流れる
🔋 電源E = 水道の水圧
高い水圧 = 強い電圧でどんどん押し込む
📌 充電 = バケツに水を溜める過程
最初はどんどん流れ込むけど、バケツが満タンに近づくにつれて流れが遅くなる
📌 放電 = バケツから水が流れ出る過程
最初は勢いよく流れ出るけど、水が減るにつれて流れが弱くなる
🔌 実際の回路で見る充放電
それでは、実際の電気回路で何が起きているか見ていきましょう。
⚡ 充電(Charging)
回路:電池E → 抵抗R → コンデンサC
何が起きる?
- スイッチを入れた瞬間:電流がたくさん流れる(コンデンサが空っぽだから)
- 時間が経つと:コンデンサに電荷が溜まってくる → 電流が減っていく
- 十分時間が経つと:コンデンサの電圧 = 電源電圧E → 電流はほぼゼロ
⚡ 放電(Discharging)
回路:充電されたコンデンサC → 抵抗R → 接地
何が起きる?
- スイッチを入れた瞬間:電流がたくさん流れる(コンデンサが満タンだから)
- 時間が経つと:コンデンサの電荷が減っていく → 電流が減っていく
- 十分時間が経つと:コンデンサの電圧 = 0V → 電流はほぼゼロ
⏱️ 時定数τ(タウ)の物理的意味
📐 時定数τ = RC とは?
充放電で最も重要な概念が時定数τ(タウ)です。公式は超シンプル:
時定数τの公式
τ = R × C
単位:[Ω] × [F] = [秒]
🎯 τの物理的な意味
「時定数τ」という名前の通り、時間の単位です。でも、何の時間なのでしょうか?
💡 時定数τの正体
充電のとき:約63.2%まで充電されるのにかかる時間
放電のとき:約36.8%まで減少するのにかかる時間
なぜ「63.2%」という中途半端な数字?これは数学的な理由(e⁻¹ ≈ 0.368)からですが、試験では理由を覚える必要はありません!
🎯 試験で覚えるべきこと
✅ τ = R × C(公式)
✅ τ秒後 → 63.2%(充電)/ 36.8%(放電)
✅ Rが大きい、Cが大きい → τも大きい = ゆっくり変化
✅ Rが小さい、Cが小さい → τも小さい = 速く変化
💡 R・Cが変わるとτはどう変わる?
| 条件 | 時定数τ | 充放電の速さ |
|---|---|---|
| Rが大きい | 大きくなる ↑ | ゆっくり(細い蛇口) |
| Rが小さい | 小さくなる ↓ | 速い(太い蛇口) |
| Cが大きい | 大きくなる ↑ | ゆっくり(大きなバケツ) |
| Cが小さい | 小さくなる ↓ | 速い(小さなバケツ) |

📈 充電曲線を完全理解
📊 充電曲線のグラフイメージ
コンデンサの充電では、電圧が0Vから最終電圧Eまで、徐々に上昇していきます。このグラフの形が「充電曲線」です。
📌 充電曲線の特徴
• 最初は急速に上昇(0% → 63.2%がτ秒)
• その後、上昇が緩やかになる
• 理論的には無限時間で100%だが、実用上は5τで「ほぼ満タン」
💡 イメージ:バケツに水を溜めるとき、最初はどんどん溜まるけど、満タンに近づくと溜まるペースが遅くなる感じ!
🧮 充電の式(数学的表現)
コンデンサの電圧V(t)は、時間tの関数として以下の式で表されます:
充電の式
V(t) = E × (1 − e−t/τ)
E:電源電圧(最終的に到達する電圧)
e:自然対数の底(≈ 2.718)
t:経過時間
τ:時定数 = R × C
⚠️ でも安心してください!
試験では、この複雑な式を使わずに解ける問題がほとんどです。次に紹介する「時間とパーセンテージの対応表」を覚えるだけでOK!
🎯 試験で使える!充電率の暗記表
τの倍数ごとに、何%まで充電されるかを覚えておけば、計算問題がスラスラ解けます!
| 経過時間 | 充電率(%) | 覚え方 |
|---|---|---|
| τ | 63.2% | 最重要!必ず覚える |
| 2τ | 86.5% | ほぼ満タンに近い |
| 3τ | 95.0% | 実用上ほぼ満タン |
| 4τ | 98.2% | ほぼ完全 |
| 5τ | 99.3% | 完全と見なす |
🎓 63.2%と86.5%の覚え方
τで63.2%:「ろくさんてんに(63.2)タウで!」
2τで86.5%:「ハロー(86)ごー(5)で2タウ!」
この2つだけ覚えれば、ほとんどの問題が解けます!
💡 例題で実践:充電
【例題】抵抗R = 10kΩ、コンデンサC = 100μFの直列回路に、100Vの電源を接続した。1秒後のコンデンサの電圧を求めよ。
【解答】
ステップ1:時定数τを計算
τ = R × C = 10kΩ × 100μF = 10×10³ × 100×10⁻⁶ = 1秒
ステップ2:1秒 = 1τなので、充電率は63.2%
ステップ3:計算
V(1秒) = 100V × 0.632 = 63.2V
答え:63.2V

📉 放電曲線を完全理解
📊 放電曲線のグラフイメージ
コンデンサの放電では、電圧が最初の電圧E₀から0Vまで、徐々に減少していきます。充電曲線を上下反転させたような形です。
📌 放電曲線の特徴
• 最初は急速に減少(100% → 36.8%がτ秒)
• その後、減少が緩やかになる
• 理論的には無限時間で0%だが、実用上は5τで「ほぼ空」
💡 イメージ:バケツの水が流れ出るとき、最初はドバドバ出るけど、水が減るとチョロチョロになる感じ!
🧮 放電の式(数学的表現)
放電の式
V(t) = E₀ × e−t/τ
E₀:初期電圧(放電開始時の電圧)
充電の式との違い:「1−」がないだけ!
🎯 試験で使える!放電率の暗記表
| 経過時間 | 残存率(%) | 充電との関係 |
|---|---|---|
| τ | 36.8% | 100 − 63.2 = 36.8 |
| 2τ | 13.5% | 100 − 86.5 = 13.5 |
| 3τ | 5.0% | 100 − 95.0 = 5.0 |
| 4τ | 1.8% | 100 − 98.2 = 1.8 |
| 5τ | 0.7% | 100 − 99.3 = 0.7 |
💡 充電と放電の関係
超重要!充電率と放電の残存率は足すと100%になります!
• 充電63.2% ↔ 放電36.8%(足すと100%)
• 充電86.5% ↔ 放電13.5%(足すと100%)
つまり、充電の数字を覚えれば、放電は引き算で出る!
💡 例題で実践:放電
【例題】100Vに充電されたコンデンサ(C = 50μF)を、抵抗R = 20kΩを通して放電させる。1秒後の電圧を求めよ。
【解答】
ステップ1:時定数τを計算
τ = R × C = 20kΩ × 50μF = 20×10³ × 50×10⁻⁶ = 1秒
ステップ2:1秒 = 1τなので、残存率は36.8%
ステップ3:計算
V(1秒) = 100V × 0.368 = 36.8V
答え:36.8V
🎯 試験本番での解き方のコツ
⚡ 3ステップ攻略法
- 時定数τを計算:τ = R × C(単位に注意!kΩ、μFなど)
- 経過時間がτの何倍か確認:例:2秒でτ=1秒なら「2τ」
- 表から該当%を読み取る:充電なら63.2%、86.5%など / 放電なら36.8%、13.5%など
⚠️ よくあるミス
❌ 単位変換ミス(kΩとΩ、μFとFの混同)
❌ 充電と放電の式を逆に使う
❌ τの計算で掛け算を忘れる(RとCを足してしまう)
❌ 63.2%と36.8%を逆に覚える
❌ パーセンテージを小数に直し忘れる(63.2% → 0.632)
📋 充電・放電の完全比較表
| 項目 | 充電 | 放電 |
|---|---|---|
| 電圧の変化 | 0V → Eへ上昇 | E₀ → 0Vへ減少 |
| 公式 | V = E(1−e−t/τ) | V = E₀e−t/τ |
| τ秒後 | 63.2% | 36.8% |
| 2τ秒後 | 86.5% | 13.5% |
| 5τ秒後 | 99.3%(ほぼ満タン) | 0.7%(ほぼ空) |
| イメージ | バケツに水を溜める | バケツから水が流れ出る |
✨ まとめ:充放電は得点源にできる!
お疲れさまでした!コンデンサの充放電、イメージできましたか?😊
📌 この記事の重要ポイント
- ✅ 時定数τ = R × C(充放電の速さを決める)
- ✅ τ秒後:充電63.2% / 放電36.8%(最重要!)
- ✅ 2τ秒後:充電86.5% / 放電13.5%
- ✅ 充電と放電の%は足すと100%
- ✅ 5τで実用上「完全充電/完全放電」と見なす
充放電の問題は、「水タンクのイメージ」と「63.2%ルール」を覚えれば、指数関数を使わなくても解けます!複雑な数式に惑わされず、物理的なイメージを大切にしてください。
過去問を3〜5問解けば、出題パターンが見えてきます。「τを計算 → 何倍か確認 → 表から%を読み取る」の3ステップで確実に得点できます!💪
📌 関連記事
電験三種の勉強時間はどのくらい?|科目別の目安と効率的な学習法まとめ充放電を含む「理論」科目の学習時間配分と効率的な勉強法を解説しています。全体像を把握して、合格への最短ルートを進みましょう!
🚀 次のステップ
この記事を読んだら、すぐに過去問で実践してみましょう!
「電気はイメージが全て」を実感できるはずです。
バケツに水を溜めるイメージを思い浮かべながら、
問題を解いてみてください。
あなたの合格を心から応援しています!✨