- 「主成分得点」って結局何の数字なの?
- 固有値や寄与率はわかったけど、最終的に何を計算すればいいの?
- 散布図の点は何を表しているの?
- 主成分得点を「新しい成績表」のたとえでスッキリ理解できる
- 計算方法が具体例でわかる(掛け算と足し算だけ!)
- 散布図の読み方をマスターして、データの構造が見えるようになる
目次
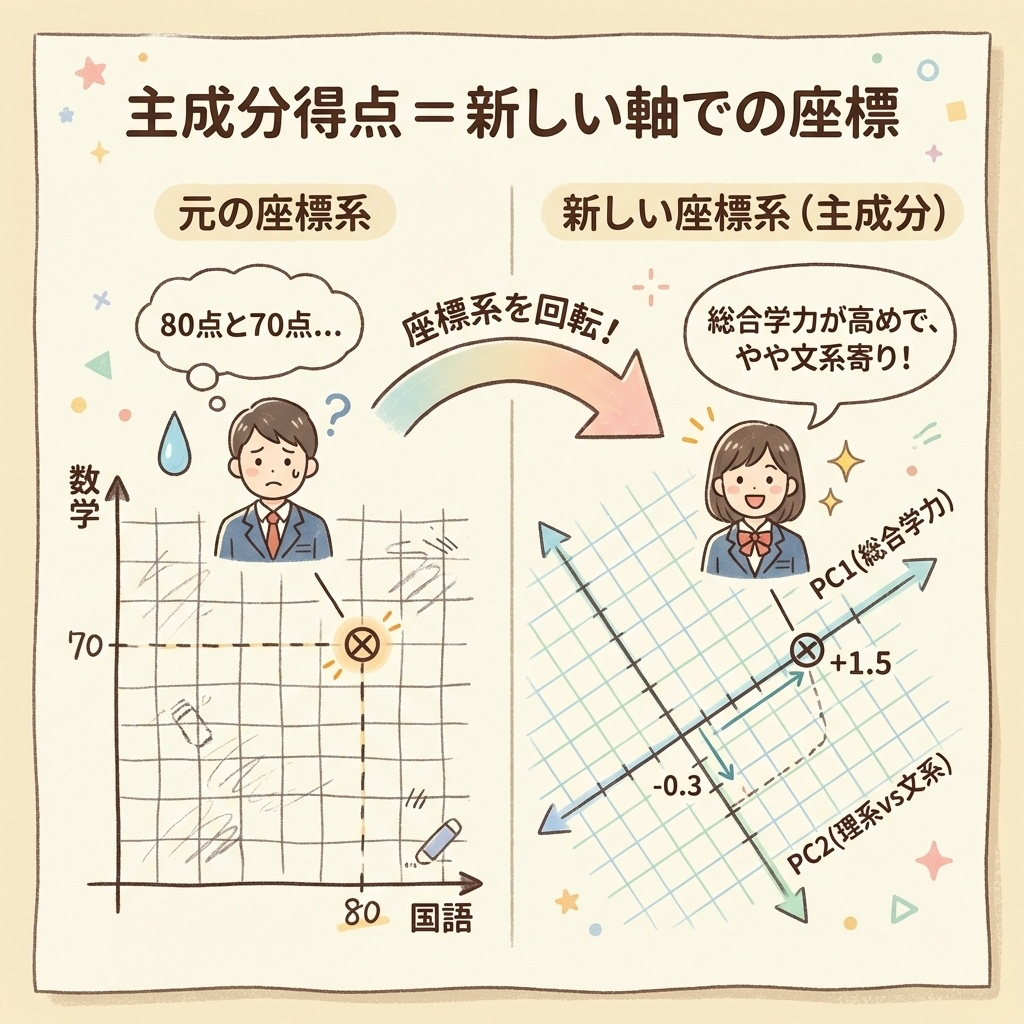
主成分得点とは?|5教科を2つの数字にまとめた「新しい成績表」
主成分分析の最後のステップが主成分得点の計算です。
これまで学んできた「固有値」「寄与率」「因子負荷量」は、新しい軸(主成分)の性質を調べるものでした。
一方、主成分得点は「各サンプル(一人一人)が、その新しい軸でどこに位置するか」を表す数字です。
主成分得点 = 各サンプルの「新しい成績表」
例えば、国語・数学・英語・理科・社会の5教科の成績があったとします。
主成分分析をすると、この5教科を「総合学力」「理系vs文系」という2つの軸にまとめることができます。
そして、各生徒のこの2軸での点数が主成分得点です。
| 生徒 | 元の成績(5科目) | → | 主成分得点(2つ) |
|---|---|---|---|
| Aさん | 国80, 数70, 英75, 理65, 社80 | → | 総合学力: +1.5 理系vs文系: -0.3 |
Aさんは「総合学力が平均より高め(+1.5)で、やや文系寄り(-0.3)」ということが、たった2つの数字でわかるのです!
地図で理解しよう|場所は同じでも座標が変わる
主成分得点のイメージをつかむために、地図を考えてみましょう。
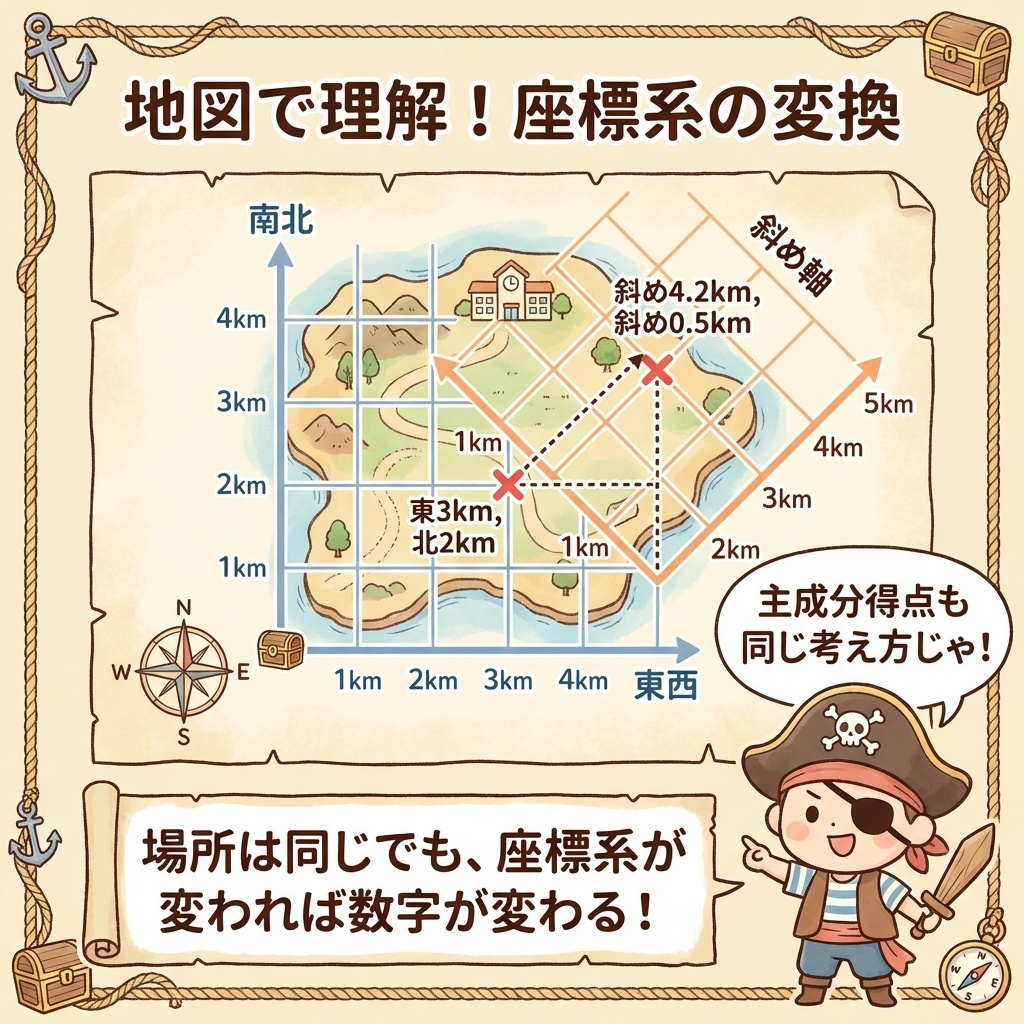
学校の位置を「東西・南北」で表すと(東3km, 北2km)。
でも、座標系を45度回転させた「斜め軸」で表すと(4.2km, 0.5km)になります。
場所(データ)は同じでも、座標系(軸)が変われば数字が変わる。
これが主成分得点のイメージです!
主成分分析では、元の軸(国語・数学・英語…)を回転させて、新しい軸(PC1・PC2…)を作ります。
その新しい軸での座標が主成分得点というわけです。
主成分得点の3つの特徴|これだけ押さえよう
主成分得点には、3つの大きな特徴があります。

特徴① 人によって違う値
主成分得点は、各サンプル(一人一人)の「立ち位置」を表す。
Aさん、Bさん、Cさんは、それぞれ違う主成分得点を持つ。
特徴② 元のデータから計算される
元の変数(国語、数学、英語…)の値に「重み」を掛けて足し合わせて計算する。
計算自体は掛け算と足し算だけ!
特徴③ 主成分の数だけ得点がある
PC1得点、PC2得点、PC3得点…というように、主成分の数だけ得点がある。
でも普通はPC1とPC2の2つだけを使うことが多い。
主成分得点の計算方法|掛け算と足し算だけ!
主成分得点の計算は、難しそうに見えて実はとてもシンプルです。

標準化データ:元のデータを「平均0、標準偏差1」に揃えたもの
固有ベクトル:前回学んだ「コンパス」(主成分の方向を決める係数)
計算例|3人の学生で実際にやってみよう
以下のテストデータで、主成分得点を計算してみましょう。
| 学生 | 数学 | 英語 |
|---|---|---|
| A | 80点 | 70点 |
| B | 60点 | 80点 |
| C | 90点 | 60点 |
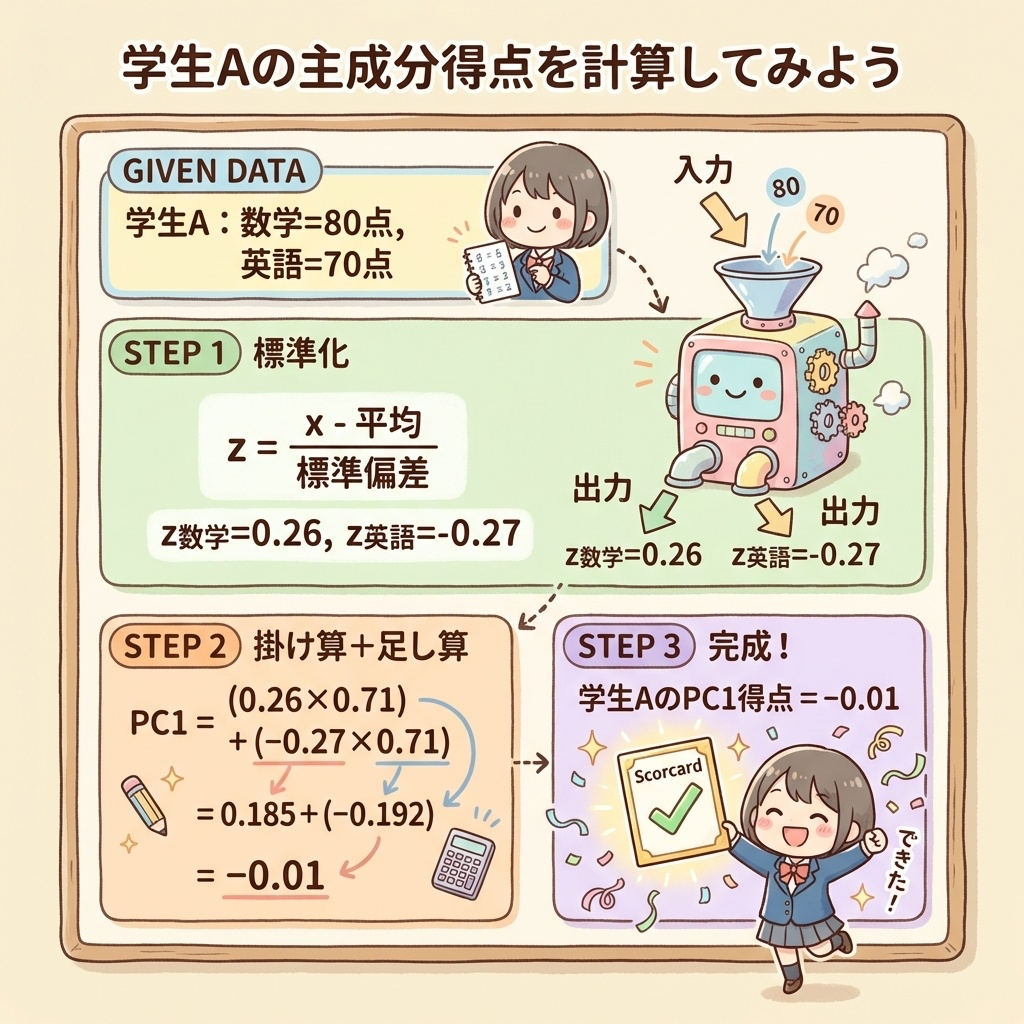
Step 1:データを標準化する
公式:z = (x - 平均) / 標準偏差
数学の標準化:z = (80 - 平均) / 標準偏差 = 0.26
英語の標準化:z = (70 - 平均) / 標準偏差 = -0.27
Step 2:固有ベクトルを用意する
PC1の固有ベクトル = [0.71, 0.71](数学と英語の重み)
Step 3:掛け算して足す
PC1得点 = (0.26 × 0.71) + (-0.27 × 0.71)
= 0.185 + (-0.192)
= -0.01
✅ 学生AのPC1得点は -0.01(ほぼ平均!)
同じ方法で全員分計算すると、以下の結果になります。

| 学生 | 元の成績 | PC1得点 | PC2得点 |
|---|---|---|---|
| A | 数学80, 英語70 | -0.01 | -0.38 |
| B | 数学60, 英語80 | -0.22 | +1.29 |
| C | 数学90, 英語60 | +0.22 | -0.91 |
・学生A:PC1もPC2もほぼ0 → バランス型
・学生B:PC2が高い → 英語寄りのタイプ?
・学生C:PC1が高く、PC2が低い → 数学寄りのタイプ?
散布図にプロットしよう|データの構造が見える!
主成分得点を計算したら、次は散布図にプロットします。
横軸にPC1、縦軸にPC2をとって、各サンプルを点として描くのです。

・似た人が近くに、違う人が遠くにプロットされる
・グループの構造が一目でわかる
・外れ値(変わった人)がすぐ見つかる
上の例では、学生Bは左上、学生Cは右下にいます。位置が離れている=特徴が違うということがわかりますね。
散布図の読み方|5つのルール
散布図からデータの構造を読み取るには、5つのルールを覚えましょう。

ルール①:近い点 = 似たサンプル
散布図上で近くにある点は、特徴が似ていることを意味します。
例えば、同じ場所に固まっている学生たちは、成績のパターンが似ているのです。
ルール②:遠い点 = 違うサンプル
逆に、離れた場所にある点は、特徴が大きく異なることを示します。

ルール③:クラスター = グループ構造
点がいくつかの「塊」に分かれていたら、それはグループ構造があるということ。
例えば「理系タイプ」「文系タイプ」「バランス型」などのグループが見えてくることがあります。
ルール④:外れ値 = 特殊なサンプル
他の点から大きく離れた点は、外れ値(異常値)の可能性があります。
特別な才能を持った人かもしれないし、データの入力ミスかもしれません。要チェック!
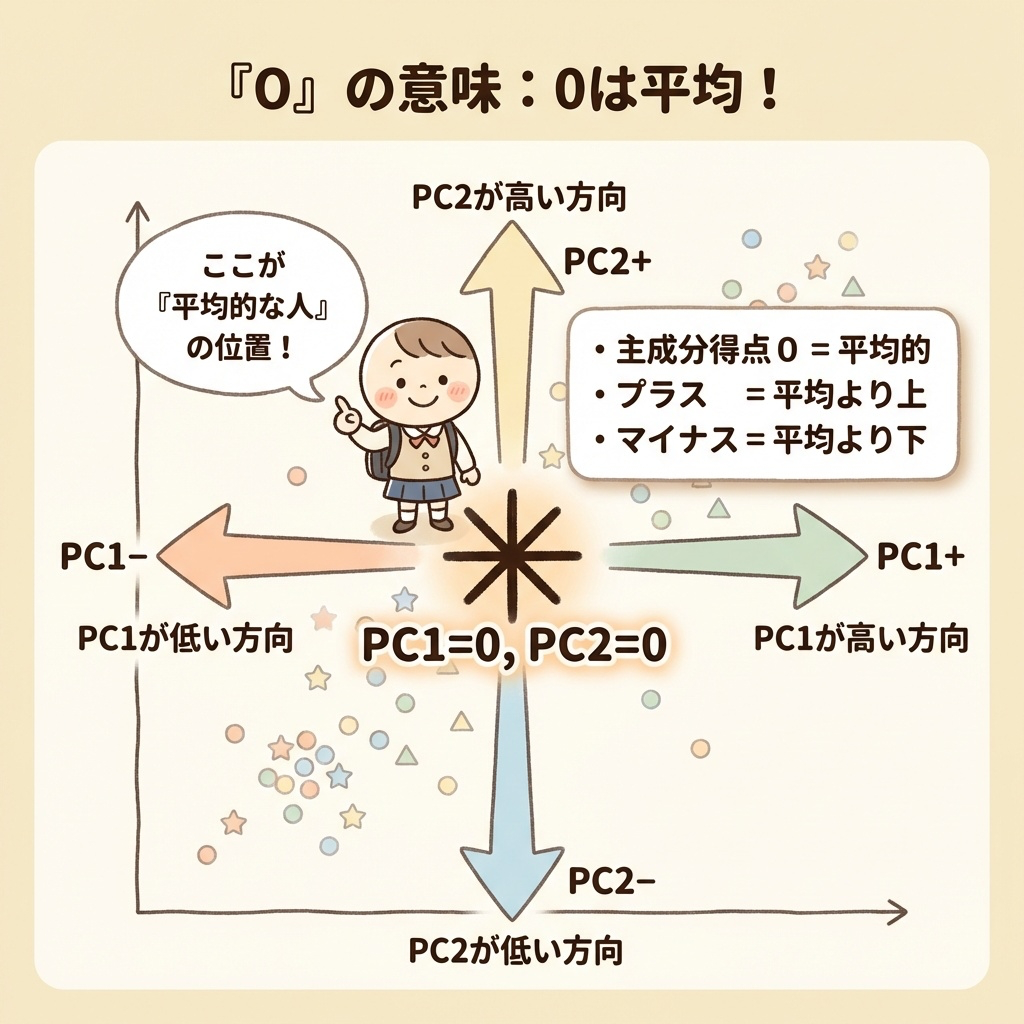
ルール⑤:0 = 平均的
主成分得点の0は「平均」を意味します。
- PC1得点 = 0 → 第1主成分について平均的
- PC1得点 がプラス → 平均より高い
- PC1得点 がマイナス → 平均より低い
散布図の原点(0, 0)付近にいる人は、「どの主成分でも平均的」ということです。
| 散布図の特徴 | 意味 |
|---|---|
| 近い点 | 似たサンプル |
| 遠い点 | 違うサンプル |
| クラスター(塊) | グループ構造がある |
| 離れた点 | 外れ値(要チェック) |
| 原点付近 | 平均的なサンプル |
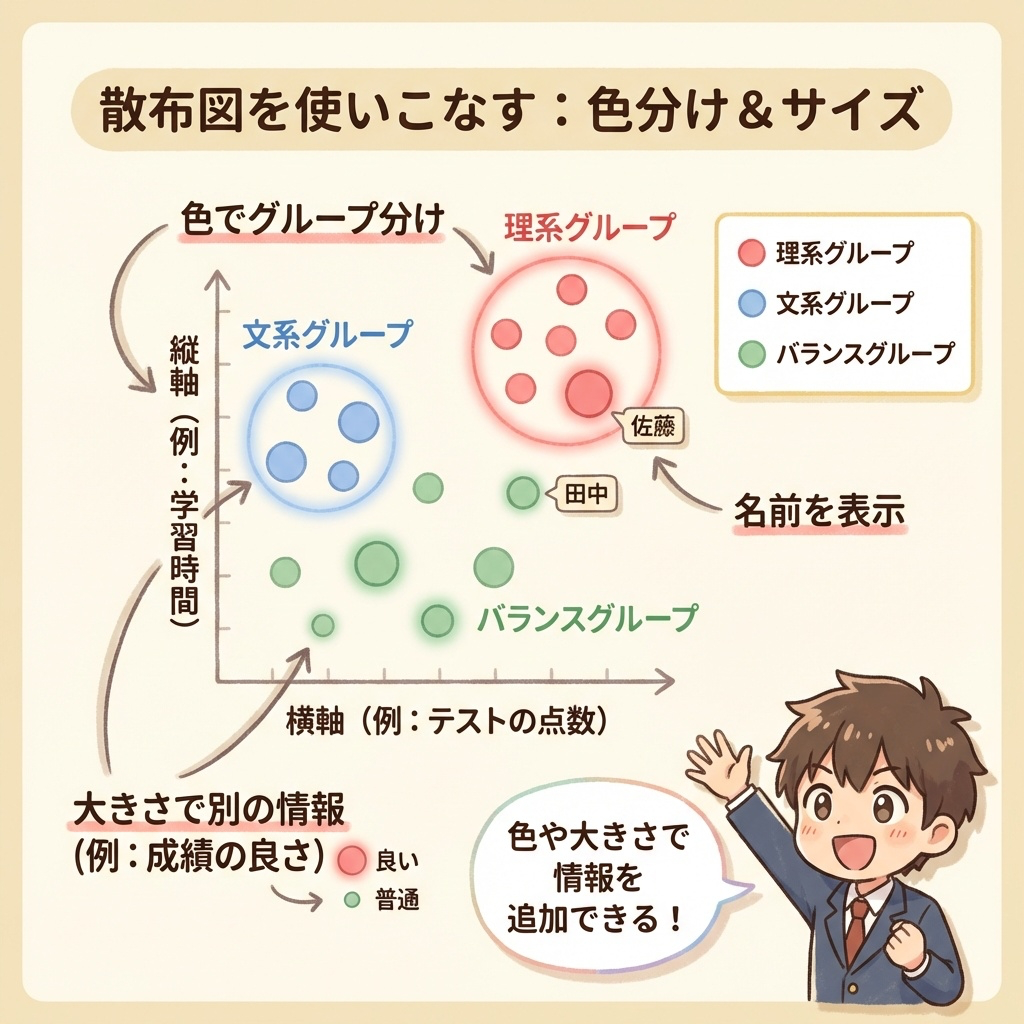
散布図をもっと使いこなす|色分け・サイズ・ラベル
基本の散布図に、さらに情報を追加することもできます。
| テクニック | やり方 | わかること |
|---|---|---|
| 色分け | グループごとに色を変える | グループの分布が見える |
| サイズ変更 | 点の大きさを変える | 3つ目の変数を表現できる |
| ラベル表示 | 点の横に名前を表示 | 個別サンプルを特定できる |
主成分分析の全体像|主成分得点は最後のステップ
主成分得点が主成分分析の中でどこに位置するか、全体像を確認しましょう。
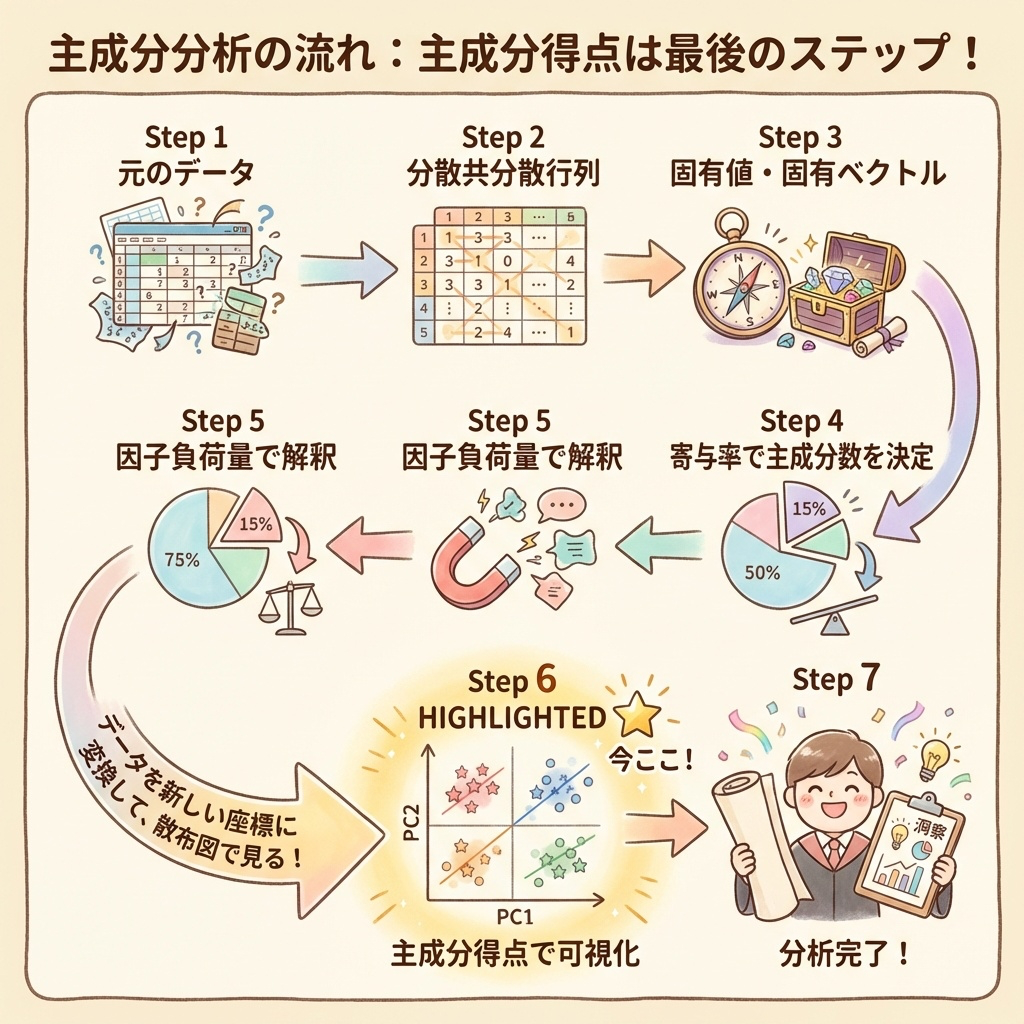
- データを集める
- 分散共分散行列(相関行列)を作る → 変数の関係を整理
- 固有値・固有ベクトルを求める → 新しい軸の方向と重要度
- 寄与率・累積寄与率を計算 → 何個の主成分を使うか決める
- 因子負荷量で解釈 → 主成分の意味を理解
- 主成分得点を計算 ← 今ここ! → 各サンプルの位置を求める
主成分得点は、主成分分析の最終アウトプットです。ここまでできれば、散布図でデータの構造を可視化できます!
まとめ|主成分得点を完全マスター!

| 項目 | 内容 |
|---|---|
| 主成分得点とは | 各サンプルの「新しい成績表」(新しい軸での座標) |
| 計算方法 | 標準化データ × 固有ベクトル を全部足す |
| 可視化 | PC1を横軸、PC2を縦軸にして散布図を描く |
| 散布図の読み方 | 近い=似てる、遠い=違う、0=平均 |
- 主成分得点 = 各サンプルの「新しい軸での座標」
- 計算は掛け算と足し算だけ(標準化データ × 固有ベクトル)
- 散布図でデータの構造が一目でわかる
- 近い点=似たサンプル、0=平均を覚えよう
📚 関連記事
因子負荷量を復習したい方はこちら。主成分の「意味」を読み取るコツがわかります。
固有値・寄与率を復習したい方はこちら。主成分の「重要度」がわかります。
主成分分析の全体像と「何のためにやるのか」を確認したい方はこちら。
【完全版】統計学の勉強ロードマップ|初心者が「データ分析」を武器にするまでの全手順 →
