😰 こんな悩み、ありませんか?
- 「位相」って言葉がそもそも意味不明
- 「遅れ」「進み」がどっちがどっちか混乱する
- ベクトル図の見方・描き方がわからない
- なぜコイルは「遅れ」でコンデンサは「進み」なの?
📌 この記事の結論
位相は「波のタイミング」、位相差は「2つの波のズレ」のこと。電圧を基準にして、電流が先に来れば「進み」、後から来れば「遅れ」。ベクトル図で考えれば一目瞭然です!
交流回路を学ぶ上で、「位相」と「位相差」の理解は避けて通れません。
でも、「位相が進む」「位相が遅れる」って言われても、ピンとこないですよね。
この記事では、波とベクトル図のイメージを使って、位相の概念を完全に理解できるように解説します。
「遅れ」と「進み」の覚え方も伝授しますので、最後まで読んでくださいね!

目次
🌊 「位相」とは何か?
まずは「位相」という言葉の意味から理解しましょう。
位相 = 波の「今どこ?」
交流は波のように変化します。サイン波(正弦波)をイメージしてください。
☕ たとえ話:1日の中の「今何時?」
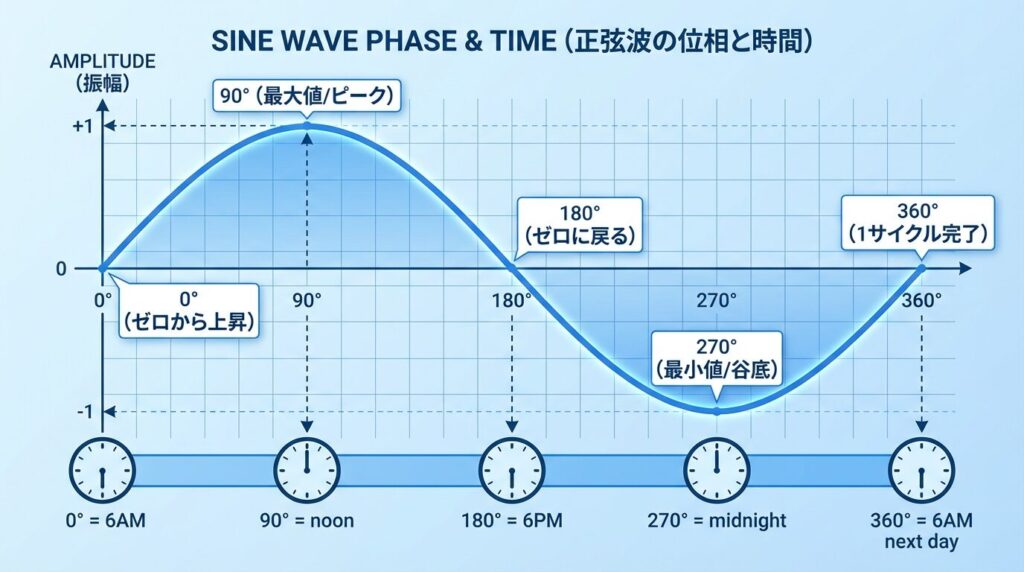
「1日」を1つのサイクルだと考えてみてください。「今、正午です」「今、夕方6時です」というのが位相です。波の中で「今どの位置にいるか」を角度(°)やラジアン(rad)で表したものが位相なのです。
位相(Phase)の定義
波の1サイクル(360° = 2π rad)の中で、
今どの位置にいるかを表す角度
サイン波の各位相を確認しよう
| 位相 | 波の状態 | イメージ |
|---|---|---|
| 0° | ゼロから上昇開始 | 朝6時(1日の始まり) |
| 90° | 最大値(ピーク) | 正午(太陽が最も高い) |
| 180° | ゼロに戻る(下降中) | 夕方6時 |
| 270° | 最小値(谷底) | 深夜0時 |
| 360° | 1サイクル完了 | 翌朝6時(次のサイクルへ) |
⏱️ 「位相差」とは何か?
次に、位相差(φ)について理解しましょう。
位相差 = 2つの波の「タイミングのズレ」
交流回路では、電圧と電流がそれぞれ波として変化しています。
この2つの波のタイミングのズレが「位相差」です。
☕ たとえ話:2人の歩き方
同じ道を歩く2人がいます。Aさん(電圧)が先に歩き始め、Bさん(電流)が少し遅れてついてきます。この「どれだけ遅れているか」が位相差です。3秒遅れなら「3秒の位相差」、角度で言えば「30°の位相差」のようになります。
位相差(φ)の定義
2つの波のタイミングのズレを角度で表したもの
単位:度(°)またはラジアン(rad)
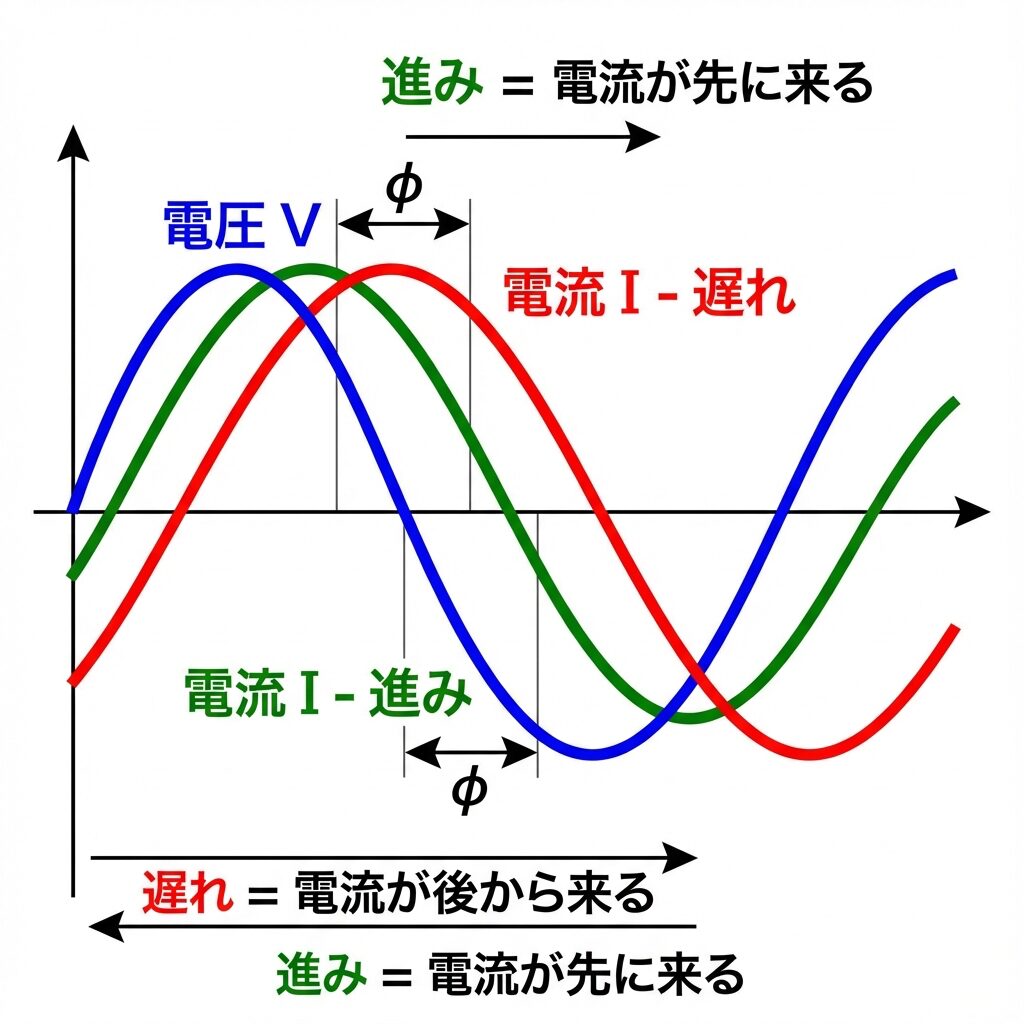
「進み」と「遅れ」の意味
位相差を語るときに必ず出てくるのが「進み」と「遅れ」です。
これは、電圧を基準にして電流を見たときの表現です。
| 用語 | 意味 | 波形のイメージ |
|---|---|---|
| 電流が進む | 電流の波が電圧より先に来る | 電流の波が左側(時間軸で手前) |
| 電流が遅れる | 電流の波が電圧より後に来る | 電流の波が右側(時間軸で後ろ) |
💡 最重要ポイント
交流回路では電圧を基準(0°)にする
電流が電圧より先 → 「進み」
電流が電圧より後 → 「遅れ」
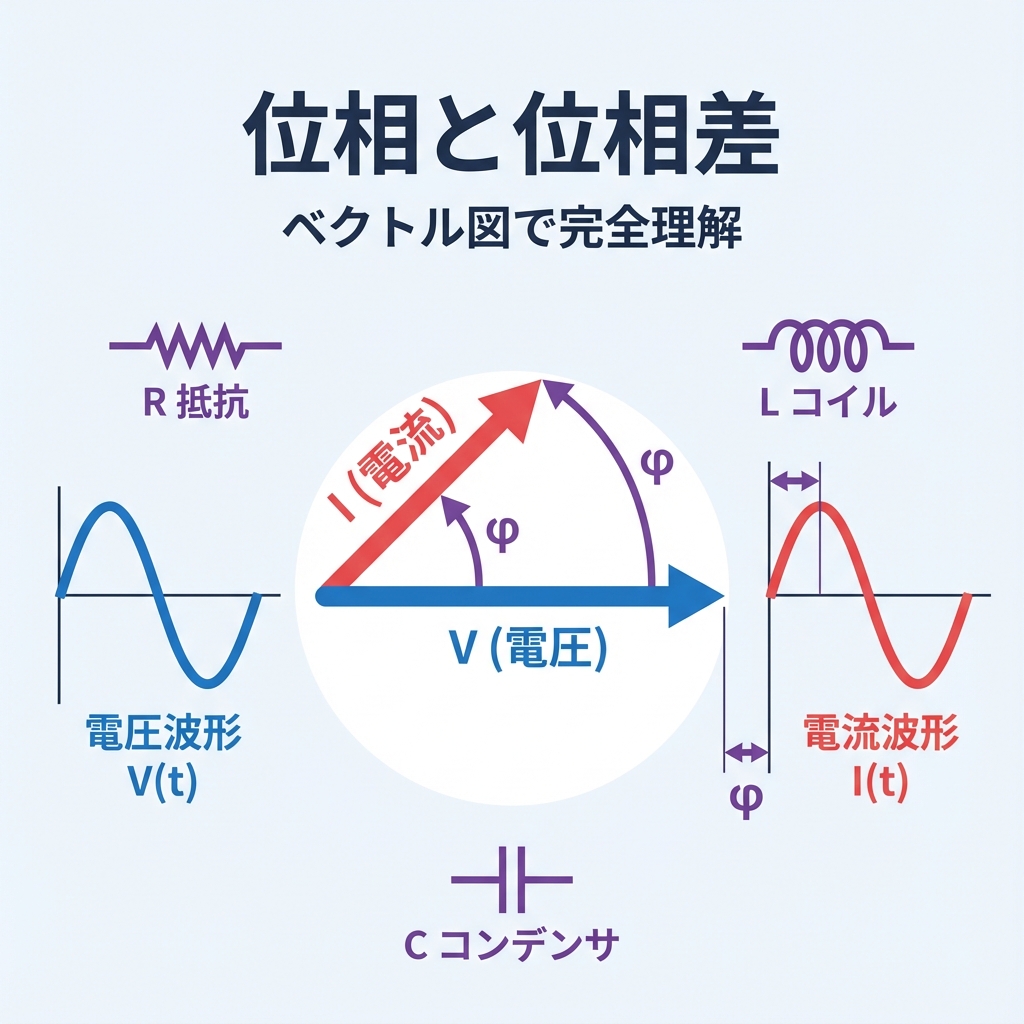
📐 ベクトル図とは?
波形を毎回描くのは大変ですよね。そこで登場するのがベクトル図です!
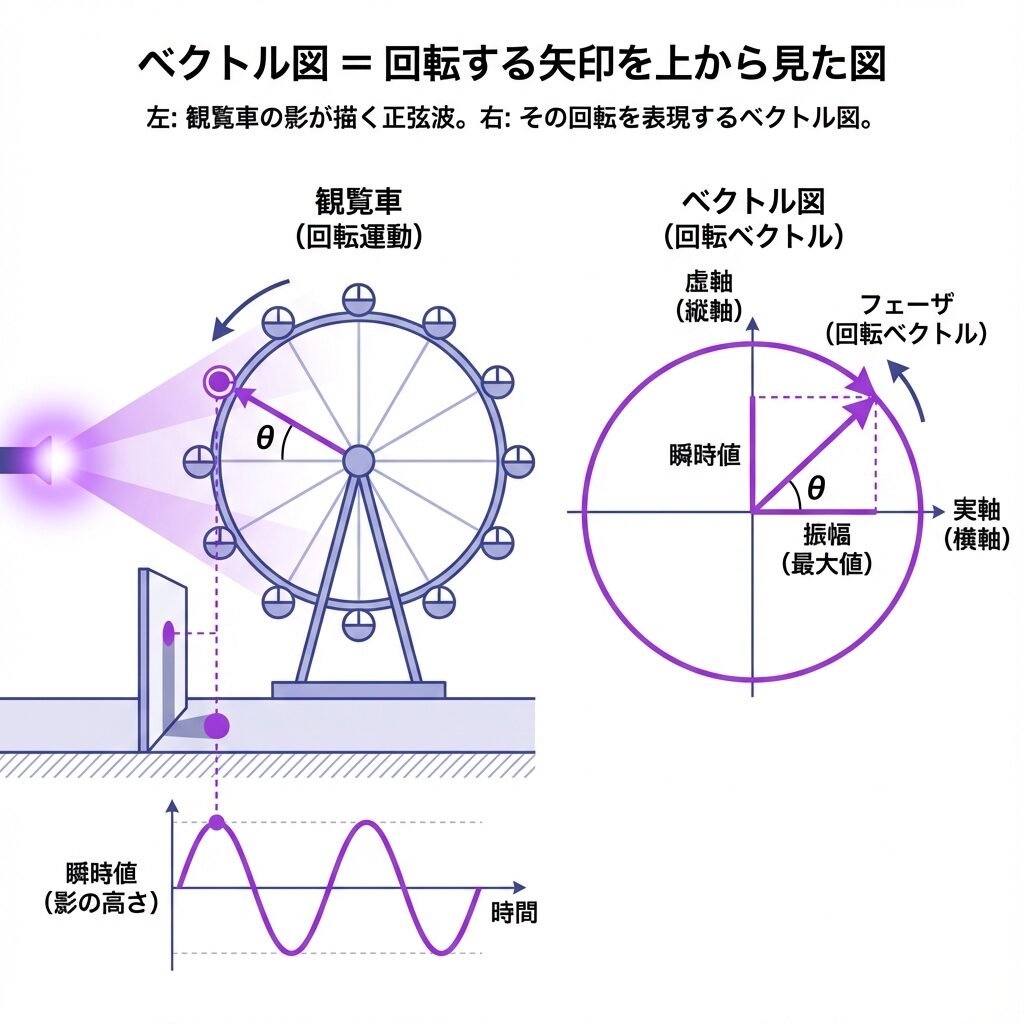
ベクトル図 = 回転する矢印で波を表す
サイン波は、実は回転する矢印(ベクトル)の影として捉えることができます。
☕ たとえ話:観覧車の影
観覧車のゴンドラが回転しているとします。横から光を当てると、地面に影ができますよね。その影は上下に動きます。この動きが「サイン波」なのです。ベクトル図は、この回転するゴンドラを真上から見た図だと思ってください。
ベクトル図の読み方
| 要素 | ベクトル図での表し方 |
|---|---|
| 大きさ(振幅) | 矢印の長さ |
| 位相 | 矢印の向き(角度) |
| 基準(0°) | 右向き(→)の水平線 |
| 回転方向 | 反時計回りが正の方向 |
🎯 覚えておくべきルール
- ベクトルは反時計回りに回転する
- 「進み」は反時計回り方向(上側)
- 「遅れ」は時計回り方向(下側)
🔄 ベクトル図で「進み」と「遅れ」を見る
ベクトル図を使うと、「進み」「遅れ」が一目で分かるようになります!
電圧を基準(右向き)に置く
交流回路のベクトル図では、電圧Vを基準として右向き(0°)に描きます。
そして電流Iを、電圧との位相差に応じて描きます。
⬆️ 電流が「進む」場合
- 電流Iは電圧Vより上側に描く
- 反時計回り方向 = 先に来る
- 例:コンデンサ回路
- 位相差:φ > 0(正)
⬇️ 電流が「遅れる」場合
- 電流Iは電圧Vより下側に描く
- 時計回り方向 = 後から来る
- 例:コイル回路
- 位相差:φ < 0(負)
なぜ上が「進み」で下が「遅れ」?
💡 理由:反時計回りが正の回転だから
ベクトルは反時計回りに回転します。だから、電圧Vより反時計回り方向(上側)にあるベクトルは、Vより「先に0°を通過する」=「進んでいる」。逆に時計回り方向(下側)にあるベクトルは「後から0°を通過する」=「遅れている」となります。

⚡ R・L・C 各回路の位相関係
ここからが超重要!各部品ごとの位相関係を見ていきましょう。
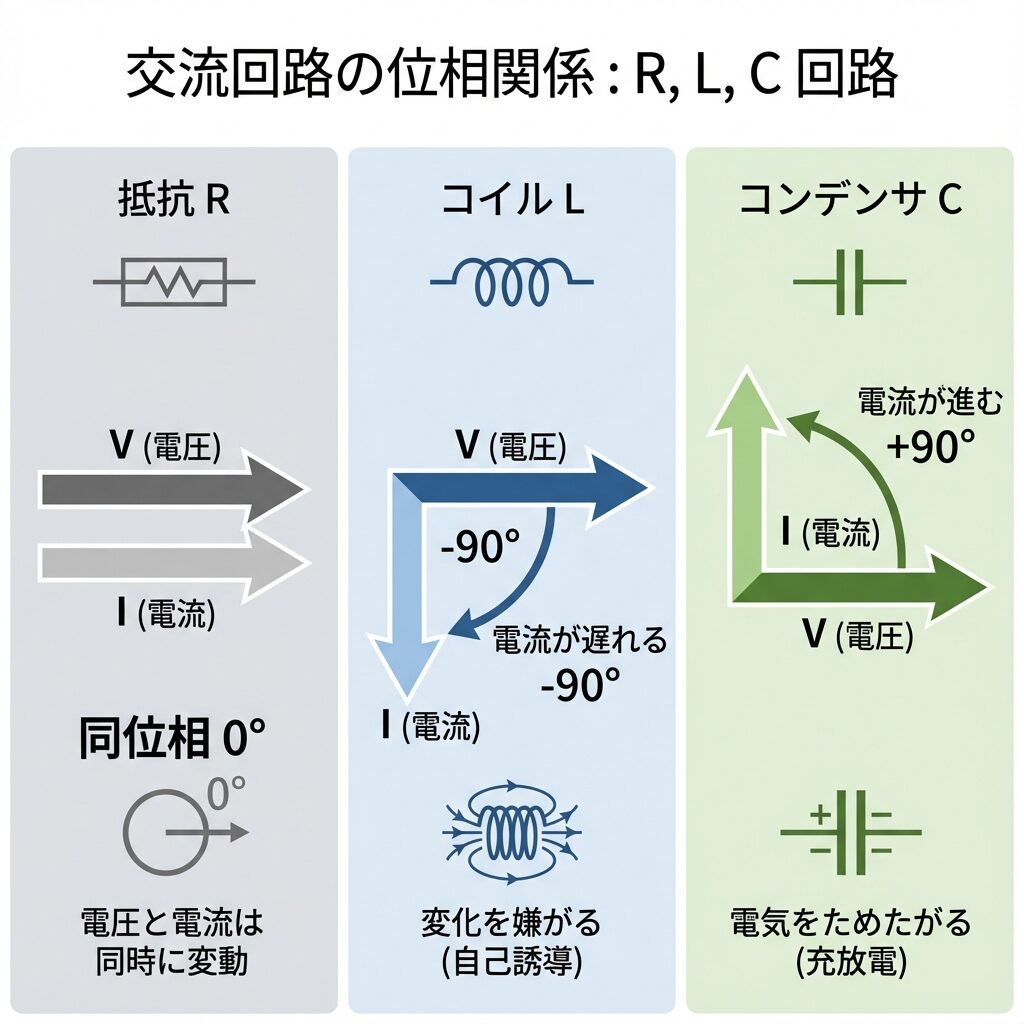
① 抵抗(R)の場合:同位相
電圧と電流は同位相(ズレなし)
位相差 φ = 0°
抵抗は電圧に対して素直に反応する。電圧が上がれば電流も上がる。
② コイル(L)の場合:電流が遅れる
電流が電圧より90°遅れる
位相差 φ = −90°
☕ なぜ遅れる?
コイルは電流の変化を嫌がる性質があります(自己誘導)。電圧をかけても「ちょっと待って!」と抵抗するので、電流が立ち上がるのに時間がかかります。
③ コンデンサ(C)の場合:電流が進む
電流が電圧より90°進む
位相差 φ = +90°
☕ なぜ進む?
コンデンサは電気を溜める性質があります。電圧をかける前から「早く電気ちょうだい!」と電流が流れ込み始めます。だから電流が電圧より先に動き出すのです。
| 部品 | 電流の位相 | 位相差 φ | ベクトル図 |
|---|---|---|---|
| 抵抗 R | 同位相 | 0° | VとI同じ向き(→) |
| コイル L | 遅れ | −90° | Iは下向き(↓) |
| コンデンサ C | 進み | +90° | Iは上向き(↑) |
🎯 「遅れ」「進み」の最強の覚え方
「コイルは遅れ?コンデンサは進み?」と混乱しがちですよね。
そこで、絶対に忘れない覚え方を伝授します!
覚え方①:語呂合わせ「コイルは遅刻」
🐌 コイルは遅刻魔
「コイル」→「こい(来い)」→「来るのが遅い」→ 遅れ
※コンデンサは逆なので「進み」
覚え方②:アルファベット順
📝 アルファベット順で覚える
C → I → L → V
コンデンサ(C)では電流(I)が先、コイル(L)では電圧(V)が先
→ Cは進み、Lは遅れ
覚え方③:イメージで覚える
🧲
コイル = 頑固おじさん
変化を嫌がって「ちょっと待て」と言う
→ 電流が遅れる
🔋
コンデンサ = 貪欲な貯金箱
「早く電気ちょうだい!」と待ち構える
→ 電流が進む

✏️ ベクトル図の描き方
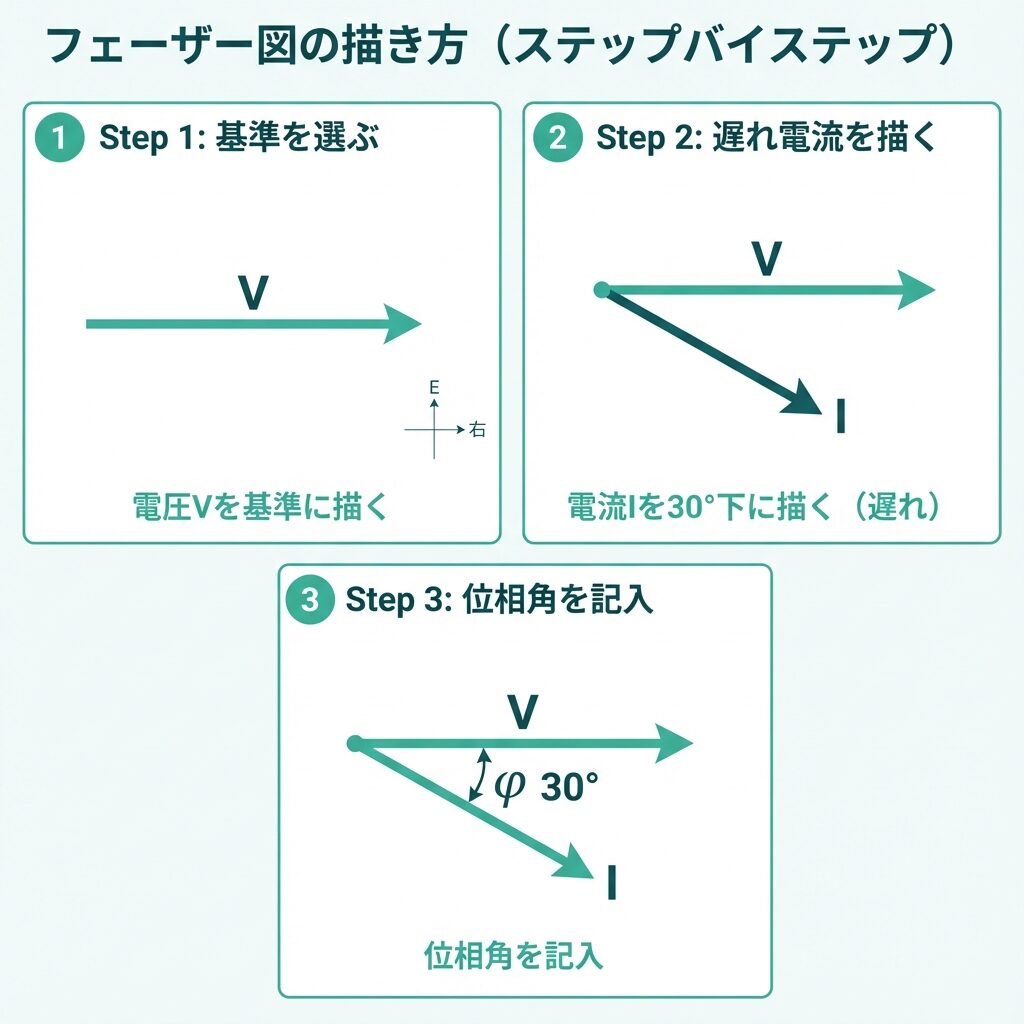
実際にベクトル図を描く手順を見ていきましょう!
ステップ1:基準を決める
まず、電圧Vを基準として水平右向き(→)に描きます。
ステップ2:電流Iを描く
電流の位相関係に応じて描きます:
- 同位相(抵抗):Vと同じ方向
- 遅れ(コイル):Vより下側(時計回り方向)
- 進み(コンデンサ):Vより上側(反時計回り方向)
ステップ3:位相角φを記入
VとIの間の角度を位相角φとして記入します。
📝 例題:R-L直列回路のベクトル図を描く
条件:電流Iが電圧Vより30°遅れている
✏️ 描き方
- 電圧Vを右向き(→)に描く
- 電流IをVより30°下側(時計回り方向)に描く
- VとIの間に「φ = 30°」と記入
※「遅れ」なので下側に描くことがポイント!
⚠️ よくある間違い
- 「遅れ」なのに上側に描いてしまう → 逆!
- 角度を反時計回りで測ってしまう → 遅れは時計回り方向
- 電流を基準にしてしまう → 基準は電圧!
📌 まとめ
この記事のポイント
- 位相:波の中で「今どの位置か」を表す角度
- 位相差(φ):2つの波のタイミングのズレ
- 基準は電圧:電流が先なら「進み」、後なら「遅れ」
- ベクトル図:回転する矢印で波を表現。反時計回りが正。
- 抵抗:同位相(0°)
- コイル:電流が90°遅れる(頑固おじさん)
- コンデンサ:電流が90°進む(貪欲な貯金箱)
📋 位相関係チートシート
| 部品 | 電流の位相 | ベクトル図の位置 |
|---|---|---|
| 抵抗 R | 同位相(0°) | →(Vと同じ) |
| コイル L | 90°遅れ | ↓(下側) |
| コンデンサ C | 90°進み | ↑(上側) |
🎯 最強の覚え方
C → I → L → V(アルファベット順)
コンデンサでは電流が先、コイルでは電圧が先
位相とベクトル図は、交流回路の基礎中の基礎です。
この記事の内容をしっかりマスターすれば、インピーダンスの計算や電力の計算もスムーズに理解できるようになります!
💡 「コイルは遅刻魔」「コンデンサは貪欲」このイメージを忘れずに!