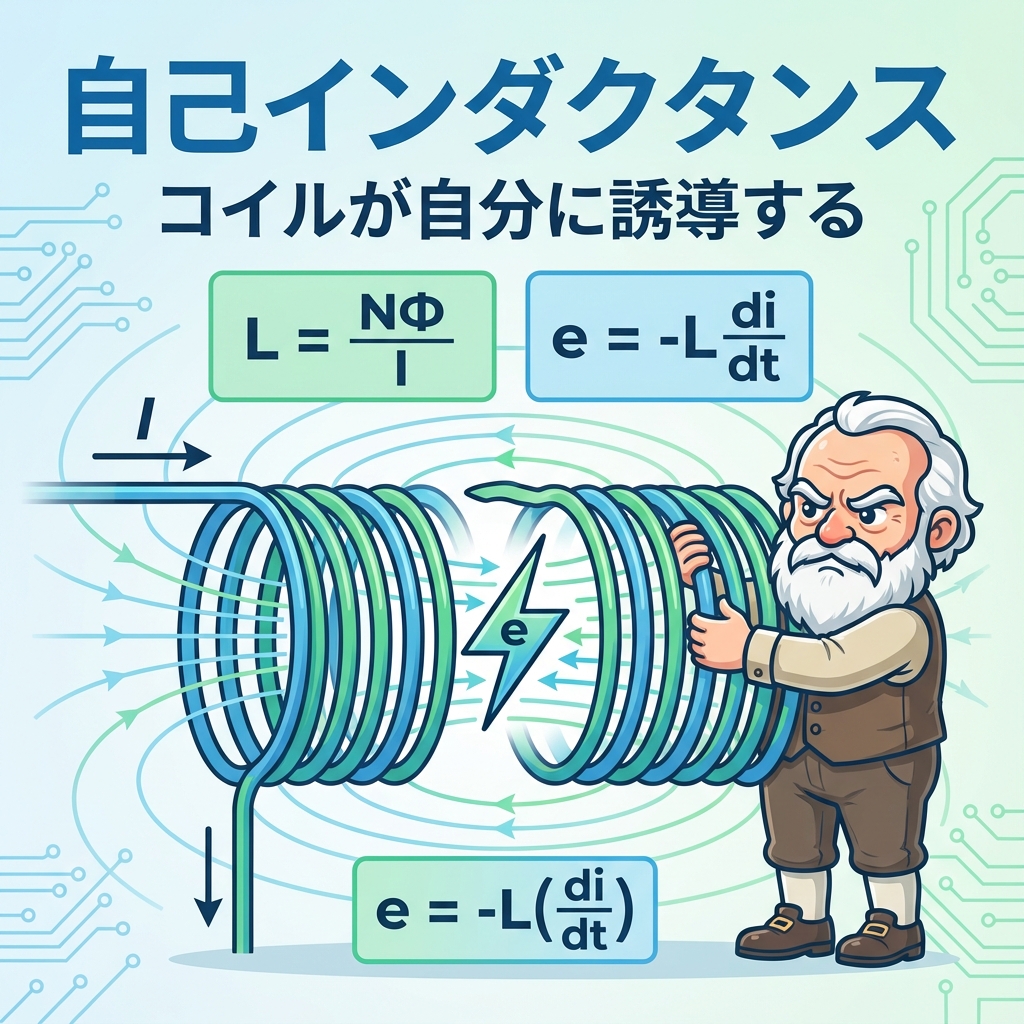
😰 こんな悩み、ありませんか?
- 「自己インダクタンス」って何のことかさっぱりわからない
- L=NΦ/I の公式が何を意味しているのかピンとこない
- e=-L(di/dt) のマイナスって何?
- なぜコイルは電流の変化を「嫌がる」の?
📌 この記事の結論
自己インダクタンスLは「コイルが電流の変化をどれだけ嫌がるか」を表す値。電流が変わろうとすると、コイルは自分で電圧を発生させて「ちょっと待て!」と抵抗します。これが自己誘導の正体です!
📚 前提知識: この記事を読む前に「電磁誘導とファラデーの法則」を読んでおくとスムーズです。
自己インダクタンスは、電験三種の理論科目で必ず出題される重要テーマです。
交流回路のリアクタンス、変圧器、電動機…すべての基礎になる概念なので、しっかり理解しておきたいですよね。
でも、「自己インダクタンス」という言葉自体が難しそうで、とっつきにくいと感じる方も多いはず。
この記事では、「頑固おじさん」のたとえ話とイメージ図解で、自己インダクタンスを完全に理解できるように解説します!
目次
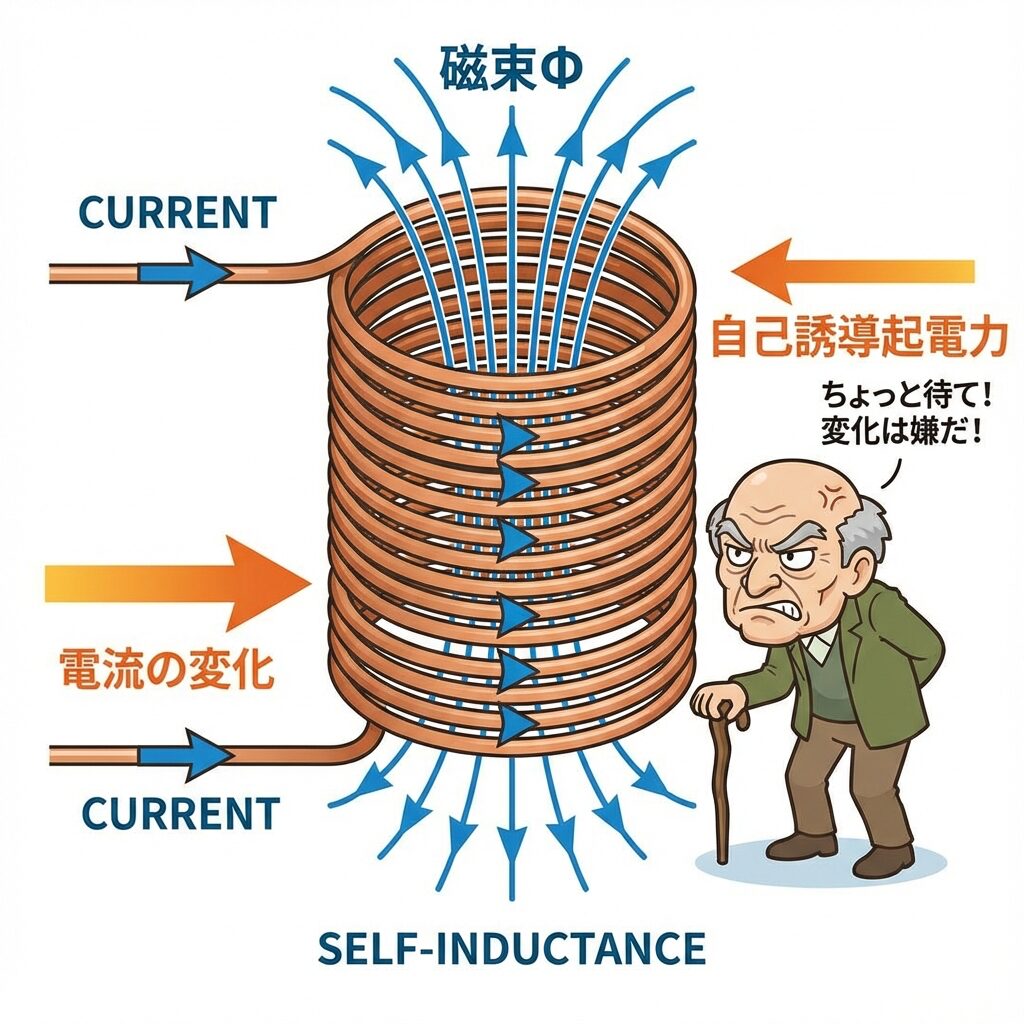
🔄 「自己誘導」とは何か?
まずは「自己誘導」という現象を理解しましょう。
コイルは「自分で自分に電圧をかける」
電磁誘導の法則では、「磁束が変化すると電圧が発生する」と学びました。
普通は、外部の磁石を動かしてコイルに電圧を誘導しますよね。
でも、コイル自身が作る磁束が変化した場合はどうでしょう?
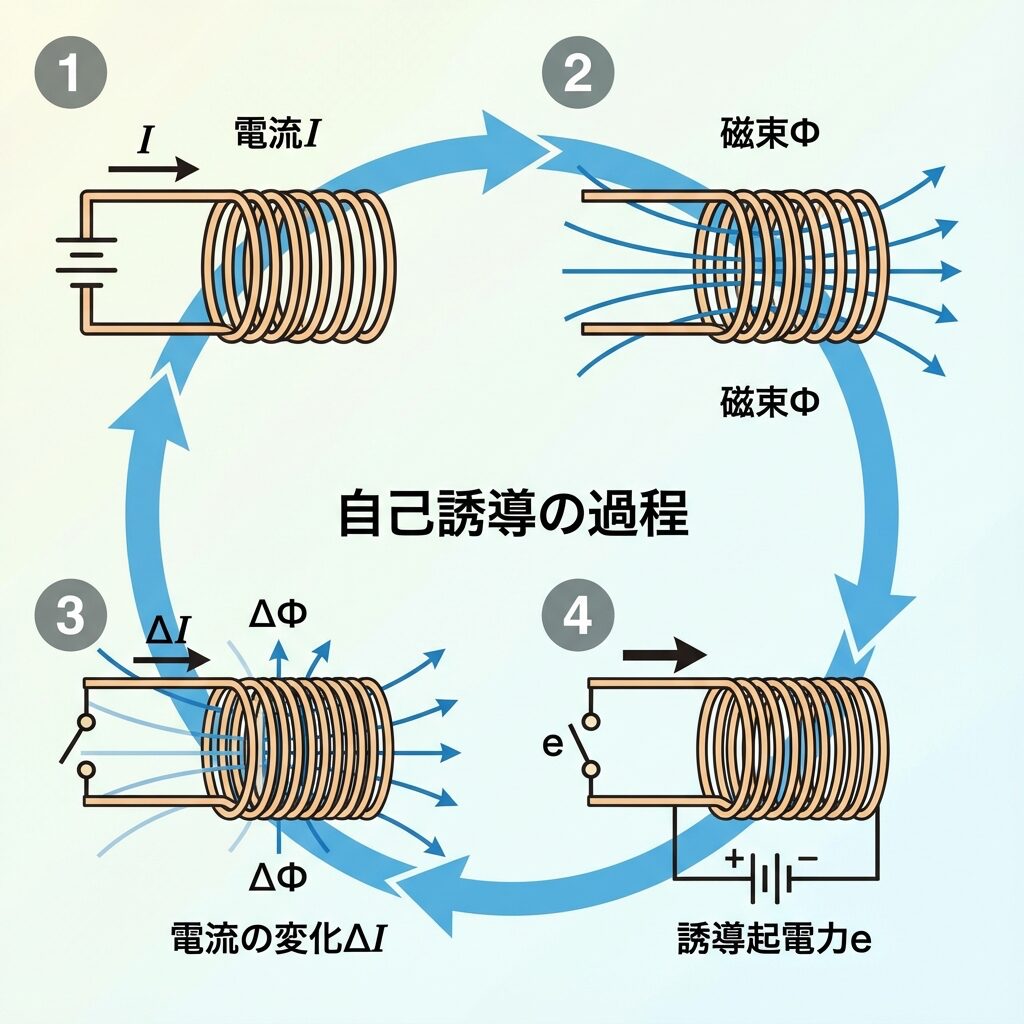
自己誘導のメカニズム
① コイルに電流を流す
↓
② コイル内に磁束が発生
↓
③ 電流が変化すると、磁束も変化
↓
④ 磁束の変化で電圧が誘導される
↓
⑤ その電圧は自分自身にかかる!
これが「自己誘導」です。外部からではなく、自分が作った磁束の変化で、自分に電圧を誘導する現象なのです。
なぜ「自己」インダクタンス?
☕ たとえ話:自分の影を踏む
太陽の下を歩くと、自分の影ができますよね。そして、その影を踏もうとすると、影も一緒に動いてしまう。自分が作り出したもの(影)が、自分自身に影響するのと同じイメージです。コイルが作った磁束が、コイル自身に電圧を誘導するのが「自己誘導」です。
ちなみに、2つのコイルが影響し合う場合は「相互誘導」と呼びます(変圧器の原理)。
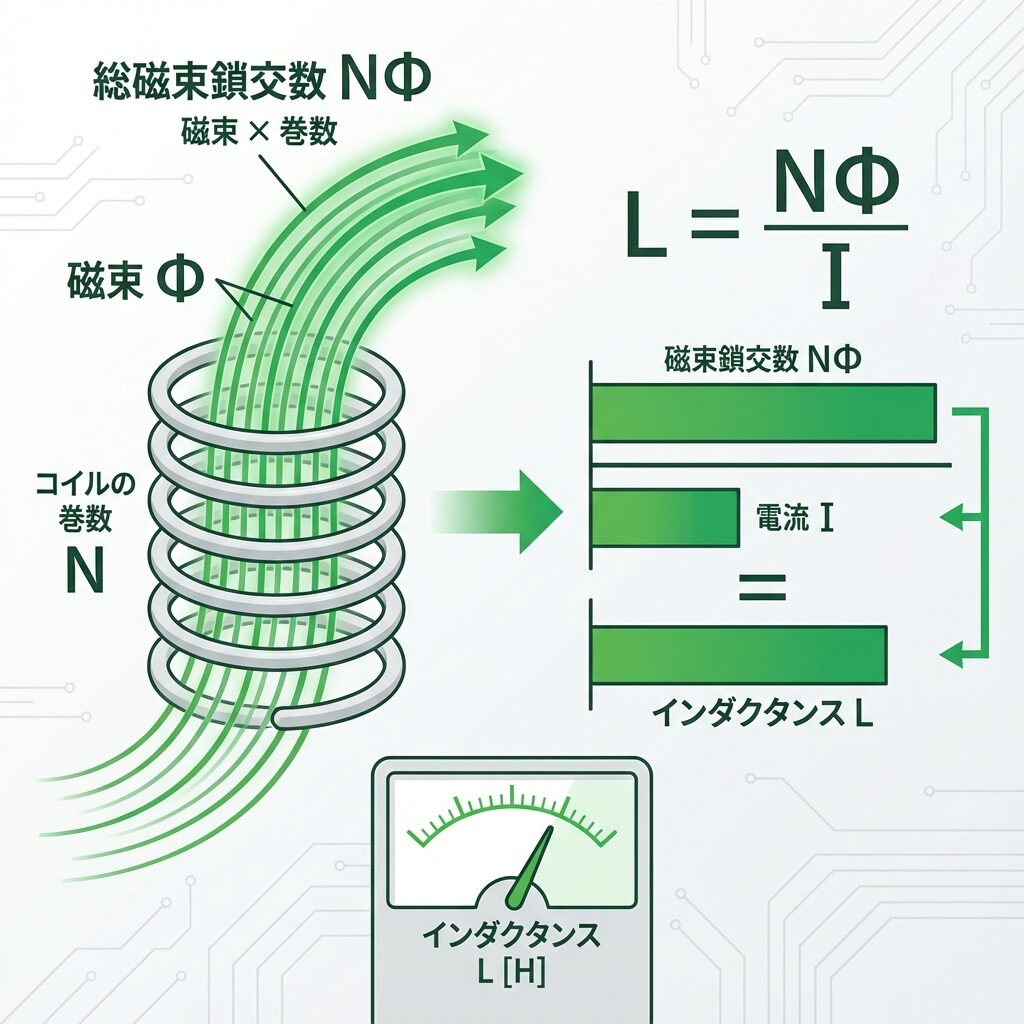
📐 自己インダクタンスLとは?
自己誘導の「強さ」を数値で表したものが自己インダクタンスLです。
Lの定義式
自己インダクタンスの定義
L = NΦ / I
L:自己インダクタンス [H](ヘンリー)
N:巻数 [回] Φ:磁束 [Wb] I:電流 [A]
この式の意味を、分解して理解しましょう。
NΦ(エヌファイ)とは?
NΦは「鎖交磁束」または「磁束鎖交数」と呼ばれます。
☕ たとえ話:輪投げのリング
コイルの各巻き(ターン)を「輪投げのリング」だと思ってください。磁束Φが各リングを貫いています。巻数Nが多いほど、磁束が貫くリングの数が増える。NΦ = 磁束×リングの数 = 全体で磁束がどれだけ「絡んでいるか」を表します。
L = NΦ/I の意味
式を言葉にすると:
「1アンペアの電流で、どれだけの磁束鎖交を作れるか」
= コイルが磁束を作る能力
= 電流変化への抵抗力
Lが大きいコイルほど、電流1Aあたりで多くの磁束を作れる = 電流の変化を強く嫌がる「頑固なコイル」ということです。
🧮 Lを「コイルの形」から計算する
L = NΦ/I は定義式ですが、実際の計算ではコイルの構造からLを求めることが多いです。
ソレノイドコイルのインダクタンス
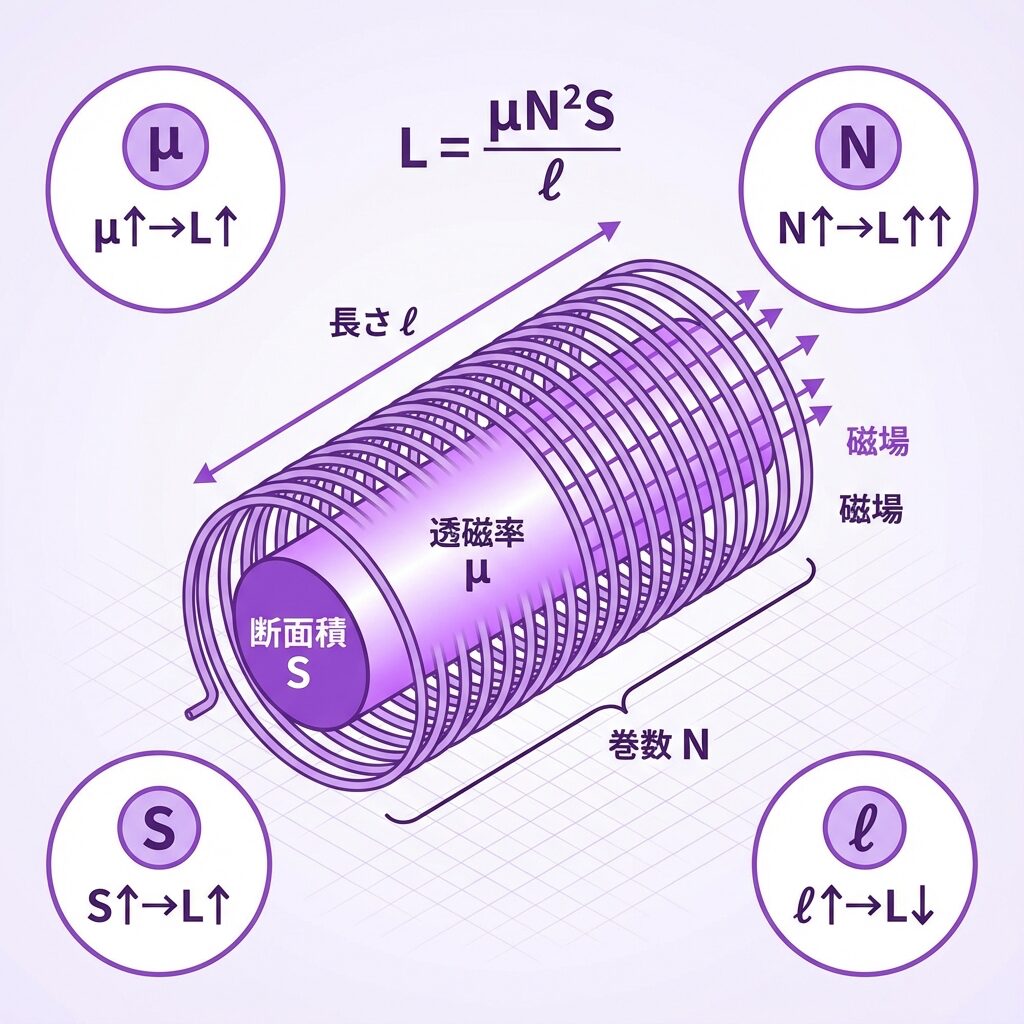
ソレノイドの自己インダクタンス
L = μN²S / l
μ:透磁率 [H/m] N:巻数 [回] S:断面積 [m²] l:長さ [m]
各要素の意味と影響
| 要素 | 記号 | Lへの影響 | イメージ |
|---|---|---|---|
| 透磁率 | μ | μ↑ → L↑ | 磁束を通しやすい材料ほど◎ |
| 巻数 | N | N↑ → L↑↑(2乗) | 巻数2倍でL4倍!最強の要素 |
| 断面積 | S | S↑ → L↑ | 太いコイルほど◎ |
| 長さ | l | l↑ → L↓ | 長いと磁束が弱まる |
🎯 最重要ポイント:N²(2乗)
巻数Nは2乗で効くことを覚えておきましょう!
巻数を2倍にすると、Lは4倍になります。試験で頻出です。
なぜN²になるのか?
💡 N²の理由
① 巻数Nが増えると、作れる磁束Φが増える(N倍)
② さらに、その磁束が貫く巻数も増える(N倍)
③ 結果:N × N = N² の効果になる!
⚡ 自己誘導起電力 e = -L(di/dt)
ここからが超重要!自己インダクタンスLを使って、誘導される電圧を計算します。
自己誘導起電力の公式
自己誘導起電力
e = -L × (di/dt)
e:誘導起電力 [V] L:自己インダクタンス [H]
di/dt:電流の時間変化率 [A/s]
公式の意味を分解する
この式を言葉で表すと:
誘導起電力 e = コイルの頑固さ(L) × 電流の変化速度(di/dt)
つまり:
・Lが大きい → 大きな電圧が発生(頑固なコイル)
・di/dtが大きい → 大きな電圧が発生(急激な変化)
マイナス(-)の意味
式の最初にある「-」がポイントです!
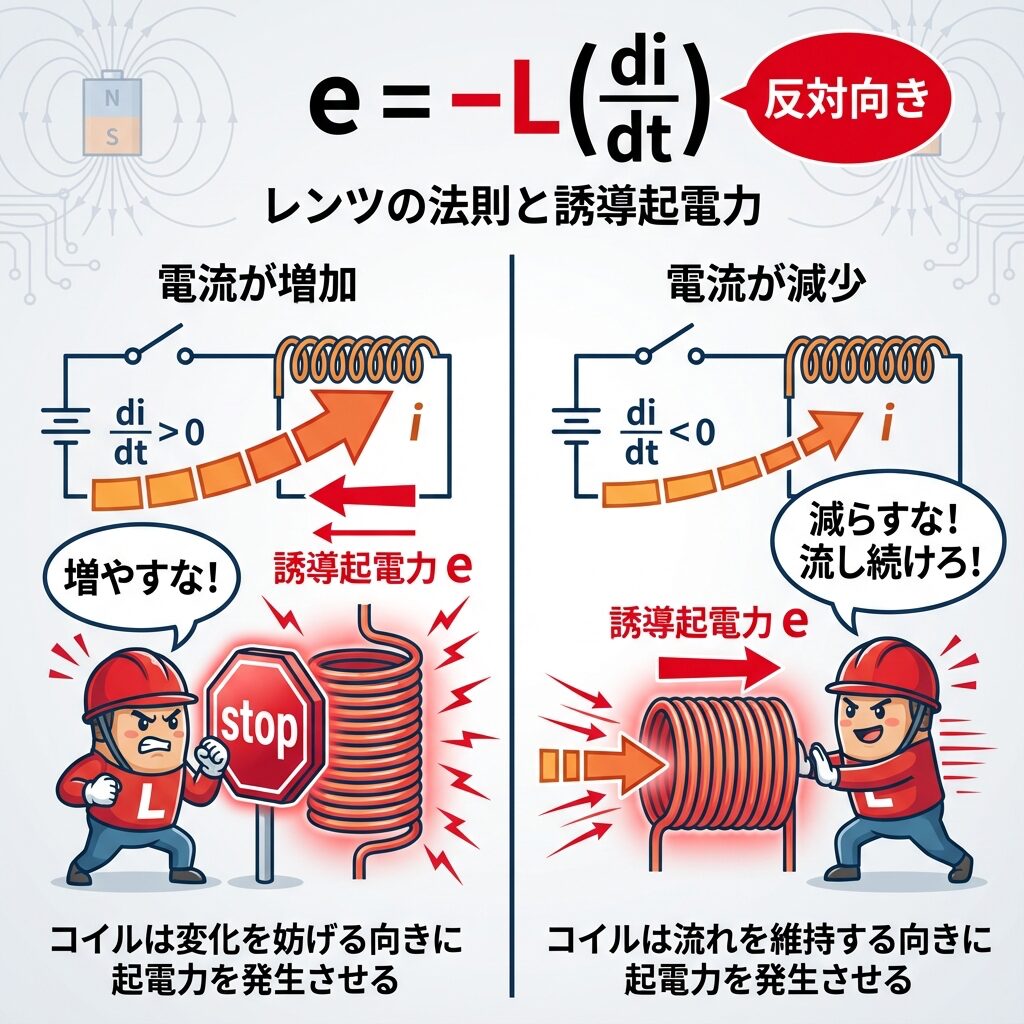
☕ たとえ話:頑固おじさんの抵抗
電流を増やそうとすると、コイルは「増やすな!」と逆向きの電圧を発生させて抵抗します。電流を減らそうとすると、「減らすな!」と流れ続けさせようとする電圧を発生させます。
この「変化を打ち消そうとする向き」を表すのがマイナスです。これはレンツの法則そのものです!
| 電流の変化 | di/dt | 誘導起電力eの向き | コイルの行動 |
|---|---|---|---|
| 電流が増加 | 正(+) | 負(-)=逆向き | 「増やすな!」と抵抗 |
| 電流が減少 | 負(-) | 正(+)=同じ向き | 「減らすな!」と流し続ける |
🧮 計算例で確認しよう
公式を使って、実際に計算してみましょう!
例題1:自己インダクタンスLを求める
📝 問題
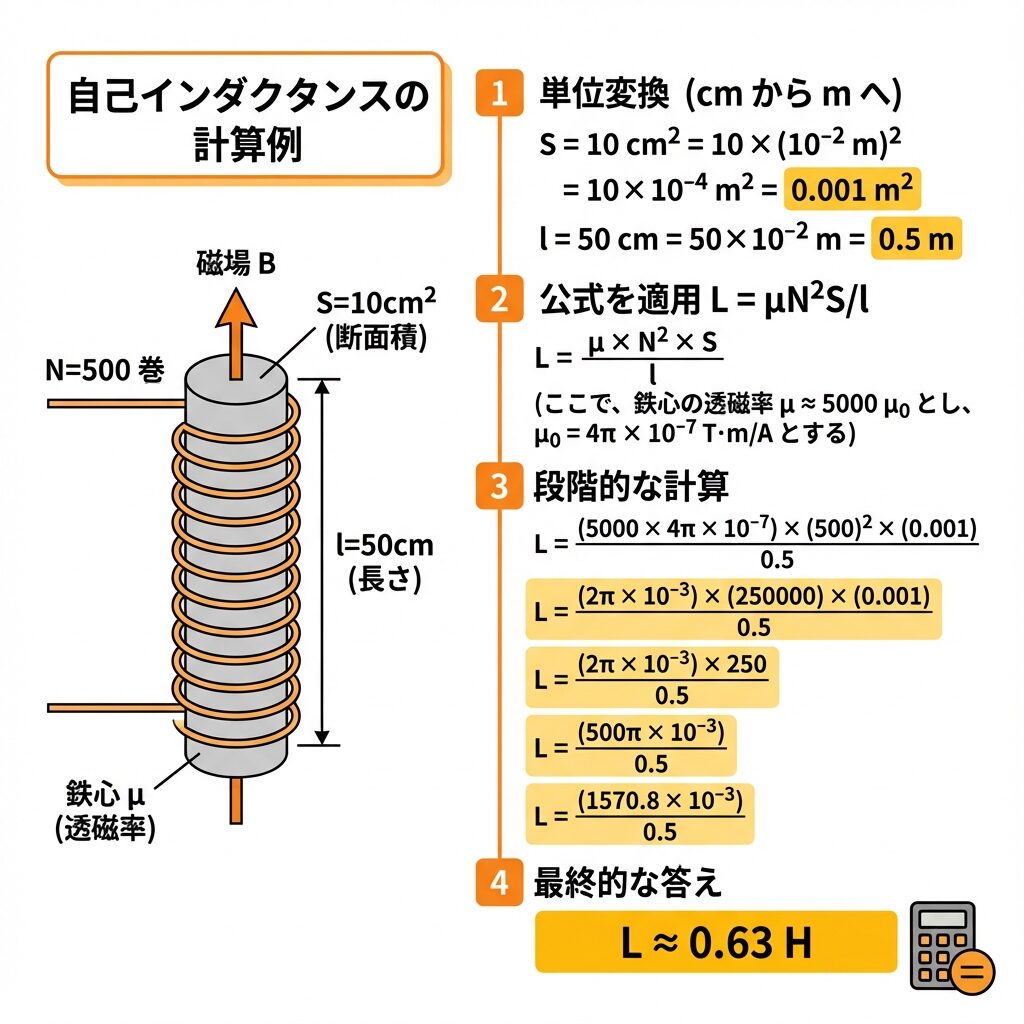
巻数 N = 500回、断面積 S = 10cm²、長さ l = 50cm のソレノイドコイルがある。
鉄心(透磁率 μ = 4π×10⁻⁴ H/m)を入れたときの自己インダクタンス L を求めよ。
✏️ 解答
まず単位を揃える:
S = 10cm² = 10×10⁻⁴ m² = 1×10⁻³ m²
l = 50cm = 0.5m
公式に代入:
L = μN²S / l
L = (4π×10⁻⁴) × 500² × (1×10⁻³) / 0.5
L = (4π×10⁻⁴) × 250000 × (1×10⁻³) / 0.5
L = (4π×10⁻⁴) × 500
L = 2π×10⁻¹ ≈ 0.628 H
∴ L ≈ 0.63 H(または 630 mH)
例題2:自己誘導起電力を求める
📝 問題
自己インダクタンス L = 0.2H のコイルに流れる電流が、0.1秒間に 2A から 5A に変化した。
このとき発生する自己誘導起電力 e を求めよ。
✏️ 解答
電流の変化率を求める:
di/dt = (5 - 2) / 0.1 = 3 / 0.1 = 30 A/s
公式に代入:
e = -L × (di/dt)
e = -0.2 × 30
e = -6 V
∴ e = -6 V(マイナスは電流増加を妨げる向き)
💡 計算のコツ
- 単位変換を忘れずに(cm→m、cm²→m²)
- di/dtは「電流の変化量÷時間」で計算
- マイナスは「逆向き」を意味するが、大きさを問われたら絶対値で答える
🔌 交流回路でのインダクタンスの役割
自己インダクタンスLは、交流回路で非常に重要な役割を果たします。
誘導性リアクタンス XL
交流回路では、コイルは「リアクタンス」という形で電流を妨げます。
誘導性リアクタンス
XL = ωL = 2πfL
XL:誘導性リアクタンス [Ω] ω:角周波数 [rad/s] f:周波数 [Hz]
この式から分かること:
📌 覚えておくべきポイント
- 周波数fが高いほど、XLは大きくなる(電流が流れにくい)
- Lが大きいほど、XLは大きくなる(頑固なコイル)
- 直流(f=0)では XL = 0 → コイルは導線と同じ(抵抗ゼロ)
なぜ周波数が高いと流れにくい?
☕ たとえ話:頑固おじさんと変化のスピード
頑固おじさん(コイル)は「変化」が嫌いです。
・ゆっくりした変化(低周波)→ なんとか我慢できる
・激しい変化(高周波)→ 「やめろー!」と全力で抵抗
だから、周波数が高いほど電流が流れにくくなるのです。
詳しくはリアクタンス(XL・XC)の記事で解説しています。
📌 まとめ
この記事のポイント
- 自己誘導:コイルが自分で作った磁束の変化で、自分に電圧を誘導する現象
- 自己インダクタンスL:「電流の変化をどれだけ嫌がるか」を表す値
- 定義式:L = NΦ / I(磁束鎖交数÷電流)
- 構造式:L = μN²S / l(巻数は2乗で効く!)
- 自己誘導起電力:e = -L(di/dt)(マイナスは逆向きを意味)
- 交流での役割:XL = 2πfL(周波数が高いほど流れにくい)
📋 公式チートシート
| 定義式 | L = NΦ / I [H] |
| 構造式(ソレノイド) | L = μN²S / l [H] |
| 自己誘導起電力 | e = -L(di/dt) [V] |
| 誘導性リアクタンス | XL = ωL = 2πfL [Ω] |
🎯 最強の覚え方
コイル = 頑固おじさん
「変化が嫌い」→ 電流が変わろうとすると逆向きの電圧で抵抗
「Lが大きいほど頑固」→ 激しく抵抗する
「周波数が高いほど激怒」→ 高周波ほど流れにくい
自己インダクタンスは、交流回路、変圧器、電動機…すべての基礎になる重要な概念です。
「頑固おじさん」のイメージで、コイルの性質をしっかり覚えておきましょう!
💡 「コイル=頑固おじさん」このイメージを忘れずに、交流回路の学習を進めましょう!