- コクランの検定が「何のための検定か」がイメージでわかる
- なぜ分散分析の「前」にこの検定が必要なのか理解できる
- F検定との違い(2群 vs 3群以上)がスッキリわかる
- 計算式の意味を「徒競走の例え」で直感的に理解できる
分散分析(ANOVA)を勉強していると、こんな注意書きに出会いませんか?
「等分散性? F検定でやるんじゃないの?」
実は、F検定は「2群」の比較にしか使えません。
では、3群以上のバラつきが揃っているかを調べたい時は?
そこで登場するのが、今回紹介する「コクランの検定(Cochran's test)」です。
コクランの検定は、
「3群以上の中に、1つだけ極端にバラつきが大きいヤツがいないか?」
を調べる検定です。
いわば、「突出した問題児」を見つける検定です。
目次
なぜ「等分散性」を確認する必要があるのか?
まず、大前提を確認しましょう。
分散分析(ANOVA)には、「各群のバラつき(分散)がだいたい同じ」という前提条件があります。
運動会の徒競走で考えてみよう
分散分析を「運動会の徒競走」に例えて説明します。
🏃 シチュエーション
3つのクラス(A組・B組・C組)の「平均タイム」を比較したい。
「どのクラスが一番速いか?」を判定する。
この時、「各クラスの中でのバラつき(実力差)」はどうあるべきでしょうか?
3クラスとも「足並みが揃っている」
→ 平均の比較が公平にできる!
C組だけ「実力差がバラバラ」
→ 平均の比較が不公平に!
C組だけ「足の速い子」と「遅い子」の差が激しいと、
平均タイムの比較が意味をなさなくなります。
「C組の平均が一番速い!」と言っても、
「それ、たまたま速い子がいただけじゃない?」とツッコまれてしまいます。
だから、「各群のバラつきが揃っているか?」を
分散分析の前に確認する必要があるのです。

コクランの検定の役割|「問題児」を見つける
では、コクランの検定は何をしているのでしょうか?
コクランの検定の目的
「3群以上の中で、
1つだけ極端にバラつきが大きい群がないか?」
を調べる検定です。
先ほどの徒競走の例で言うと、
「A組・B組・C組の中で、
C組だけ異常にバラついてない?」
を調べるのがコクランの検定です。
F検定との違い
「バラつきの比較なら、F検定でいいんじゃないの?」と思うかもしれません。
違いを整理しましょう。
| F検定 | コクランの検定 | |
|---|---|---|
| 比較する群の数 | 2群のみ | 3群以上 |
| 調べること | AとBのバラつきは 同じか? |
1つだけ極端に バラついている群はないか? |
| 使う場面 | t検定の前 | 分散分析(ANOVA)の前 |
| イメージ | 1対1の対決 | 集団の中の 「問題児探し」 |
コクランの検定は、「最大のバラつき」だけに注目します。
つまり、「一番バラついている群が、突出しているかどうか」を調べます。
「全体的にバラつきが揃っているか」を調べる検定とは少し違います。
(全体の等分散性を調べたい場合は「バートレット検定」を使います)

コクランの検定の計算式|「最大のバラつき」の割合
計算式を見てみましょう。意味が分かれば、とてもシンプルです。
コクランの統計量 G
ΣVi:各群の分散の合計
式の意味を「ケーキの分け方」で理解する
この式は、「全体のバラつきの中で、最大のバラつきがどれくらいの割合を占めるか?」を計算しています。
3人でケーキを分けることを想像してください。
理想:3人が均等に1/3ずつ = 約33%ずつ
問題:1人だけが70%も取っている!
→ 「この子だけ取りすぎじゃない?」
コクランの検定は、「最大の分散が、全体の何%を占めているか」を調べて、
その割合が大きすぎたら「問題あり!」と判定します。
具体例で計算してみよう
3つの機械(A・B・C)で製品を作り、それぞれのバラつき(分散)を計算した。
| 機械 | 分散 V |
|---|---|
| A | 10 |
| B | 12 |
| C | 38(最大) |
| 合計 | 60 |
→ 最大の分散が、全体の63.3%を占めている!
3群なら本来は33%程度のはずなのに、約2倍も占めている。
「C機だけバラつきすぎでは?」という疑いが生まれる。

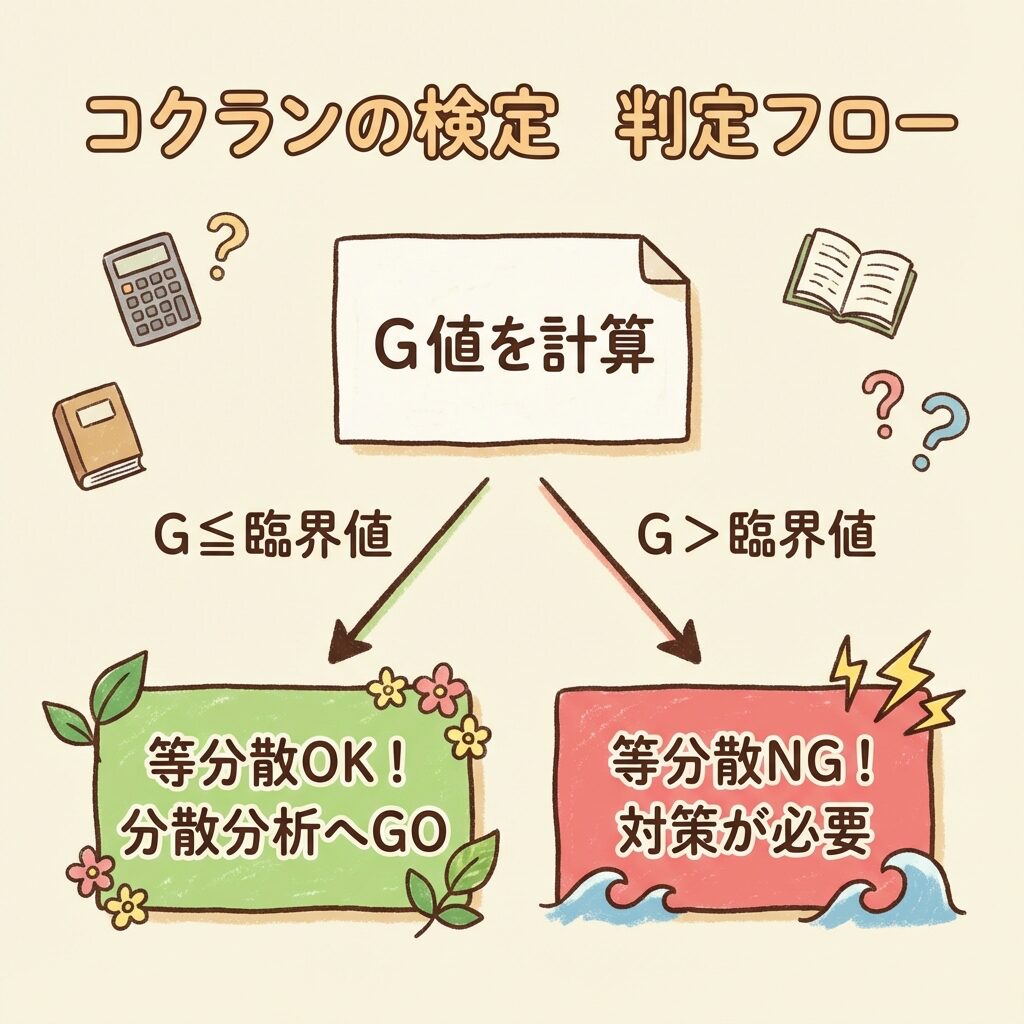
判定方法|G値を臨界値と比較する
計算したG値を、コクランの臨界値表と比較して判定します。
判定ルール
(帰無仮説を棄却しない)
→ 分散分析に進んでOK!
(帰無仮説を棄却)
→ そのまま分散分析するのは危険!
コクランの臨界値表(抜粋)
有意水準 α = 0.05 の場合の臨界値を示します。
| 群の数 k |
各群のデータ数 n | ||||
|---|---|---|---|---|---|
| 3 | 4 | 5 | 6 | 10 | |
| 3 | 0.871 | 0.798 | 0.746 | 0.707 | 0.602 |
| 4 | 0.798 | 0.684 | 0.629 | 0.590 | 0.492 |
| 5 | 0.746 | 0.629 | 0.544 | 0.507 | 0.418 |
| 6 | 0.707 | 0.590 | 0.507 | 0.469 | 0.382 |
k:比較する群の数(機械の台数など)
n:各群のデータ数(繰り返し回数など)
例:3台の機械で、各5回ずつ測定した場合
→ k=3, n=5 の交点 = 0.746 が臨界値
具体例で判定してみよう
先ほどの計算例で、実際に判定してみましょう。
ケーススタディ
- 機械の台数:k = 3
- 各機械のデータ数:n = 5
- 計算したG値:0.633
- 有意水準:α = 0.05
表から k=3, n=5 の値を探すと…
臨界値 = 0.746
G値が臨界値以下なので、
等分散とみなせる
→ 分散分析(ANOVA)に進んでOK!
等分散性が満たされていないので、以下の対応が必要です。
① データを変換する(対数変換など)
② ノンパラメトリック検定を使う(クラスカル・ウォリス検定など)
③ 問題のある群を除外して再分析
コクランの検定の使いどころ
どんな時にコクランの検定を使うのか、整理しておきましょう。
使うべき場面
- 分散分析(ANOVA)の前に等分散性を確認したい
- 3群以上のバラつきを比較したい
- 「1つだけ極端にバラついている群」がないか調べたい
- 各群のデータ数が同じ(等反復)の場合
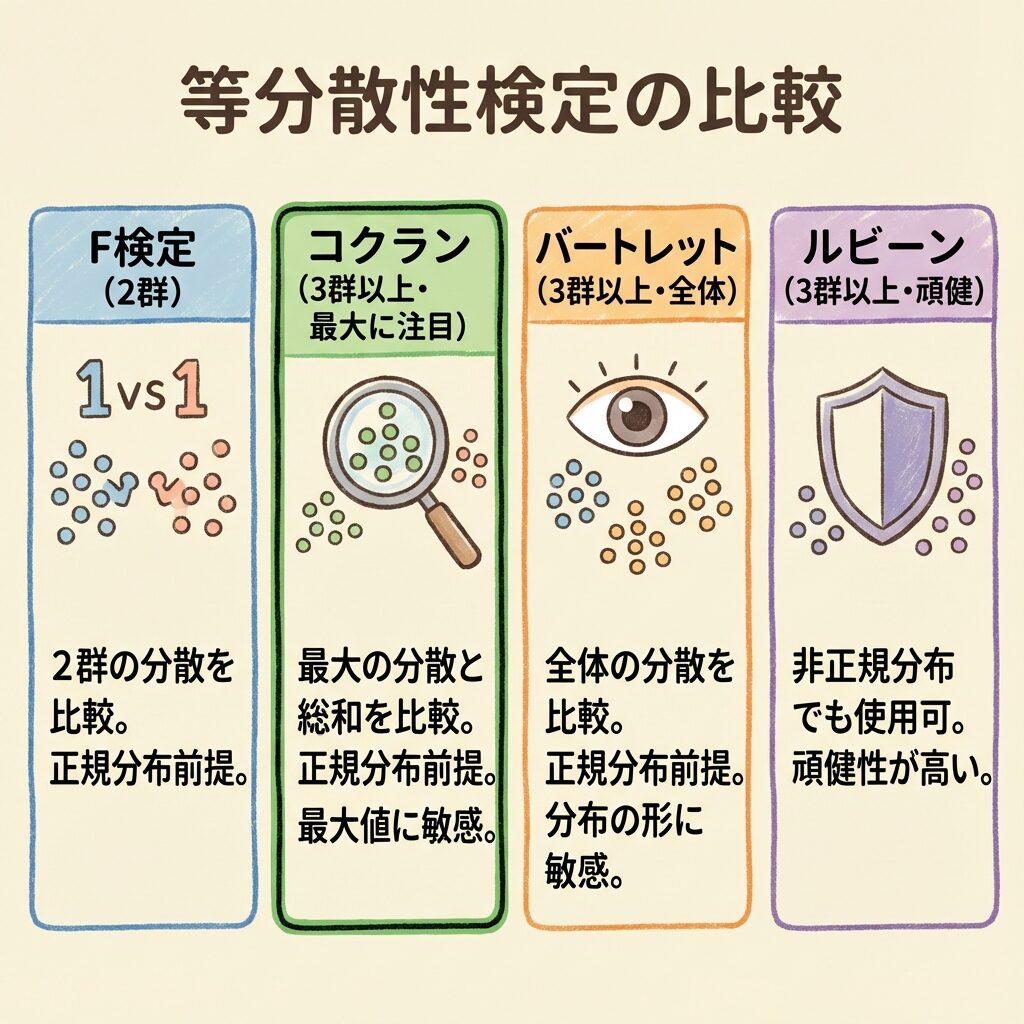
他の等分散性検定との比較
| 検定名 | 群の数 | 特徴 |
|---|---|---|
| F検定 | 2群 | 最も基本的。t検定の前に使う |
| コクランの検定 | 3群以上 | 最大の分散が突出しているかを検定 計算が簡単。等反復が条件 |
| バートレット検定 | 3群以上 | 全体の等分散性を検定 正規性に敏感で、非正規データに弱い |
| ルビーン検定 | 3群以上 | 全体の等分散性を検定 正規性に頑健で、実務で推奨される |
「1つだけ突出しているか」を調べたい → コクランの検定
「全体的にバラつきが揃っているか」を調べたい → バートレット検定 or ルビーン検定
QC検定や実験計画法では、コクランの検定がよく出題されます!
まとめ|コクランの検定は「問題児探し」
3群以上の中で、1つだけ極端にバラつきが大きい群がないかを調べる
→ 「突出した問題児」を見つける検定
G = Vmax / ΣVi
「最大の分散が、全体の何%を占めるか」を計算
→ ケーキを「取りすぎ」ている子を探すイメージ
G ≤ 臨界値 → 等分散とみなせる(分散分析OK)
G > 臨界値 → 等分散でない(対策が必要)
F検定 → 2群の比較
コクランの検定 → 3群以上の比較(最大の分散に注目)
コクラン = 「コレだけ」クランク(突出)してない?
最大のバラつきだけに注目して、「この子だけおかしくない?」を調べる検定です。
次に学ぶべきこと
コクランの検定で「等分散性OK」と確認できたら、いよいよ分散分析(ANOVA)に進みましょう。
分散分析では、「3群以上の平均に差があるか?」を判定します。
💪 ここまで読んでくださった方へ
「コクランの検定」、
「問題児探し」のイメージで覚えられましたね!
等分散性の検定は、分散分析の「前座」として地味ですが、
これをサボると分析結果の信頼性がガタ落ちします。
「バラつきの足並みを揃える」という発想を忘れずに、
正しい分析を心がけましょう!
統計学のおすすめ書籍
統計学の「数式アレルギー」を治してくれた一冊
「Σ(シグマ)や ∫(インテグラル)を見ただけで眠くなる…」 そんな私を救ってくれたのが、小島寛之先生の『完全独習 統計学入門』です。
この本は、難しい記号を一切使いません。 「中学レベルの数学」と「日本語」だけで、検定や推定の本質を驚くほど分かりやすく解説してくれます。
「計算はソフトに任せるけど、統計の『こころ(意味)』だけはちゃんと理解したい」 そう願う学生やエンジニアにとって、これ以上の入門書はありません。
【QC2級】「どこが出るか」がひと目で分かる!最短合格へのバイブル
私がQC検定2級に合格した際、使い倒したのがこの一冊です。
この本の最大の特徴は、「各単元の平均配点(何点分出るか)」が明記されていること。 「ここは出るから集中」「ここは出ないから流す」という戦略が立てやすく、最短ルートで合格ラインを突破できます。
解説が分かりやすいため、私はさらに上の「QC1級」を受験する際にも、基礎の確認用として辞書代わりに使っていました。 迷ったらまずはこれを選んでおけば間違いありません。


