- 「偏回帰係数って何?普通の回帰係数と何が違うの?」
- 「"他の変数を固定したとき"って、どういう意味?」
- 「なぜ"偏"という字がつくの?」
- 偏回帰係数の意味をイメージで完全理解
- 「他を固定したとき」を身近な例で納得
- 単回帰の回帰係数との決定的な違い
- 偏回帰係数がなぜ重要なのか
重回帰分析を学ぶと、必ず出てくる「偏回帰係数」という言葉。
「偏」という字が難しそうで、苦手意識を持っている方も多いのではないでしょうか?
でも安心してください。偏回帰係数の考え方は、実はとてもシンプルです。
この記事では、「マンション価格」「ダイエット」「テストの点数」など身近な例をたくさん使って、偏回帰係数の意味を徹底的に解説します。
【超入門】重回帰分析とは?|複数の要因で結果を予測する仕組み →
目次
🎯 偏回帰係数を一言でいうと?
まず、結論から言います。
「他の説明変数を固定したとき」に、その説明変数が1単位増えると、目的変数がどれだけ変化するかを表す数値です。
「他の説明変数を固定したとき」がポイントです。
これだけだとピンと来ないと思うので、具体例で説明しましょう。
🏠 具体例①:マンション価格で理解する
マンション価格を予測する重回帰式を考えてみましょう。
(単位:価格=万円、面積=㎡、駅徒歩分=分、築年数=年)
この式の+50、−30、−20が「偏回帰係数」です。
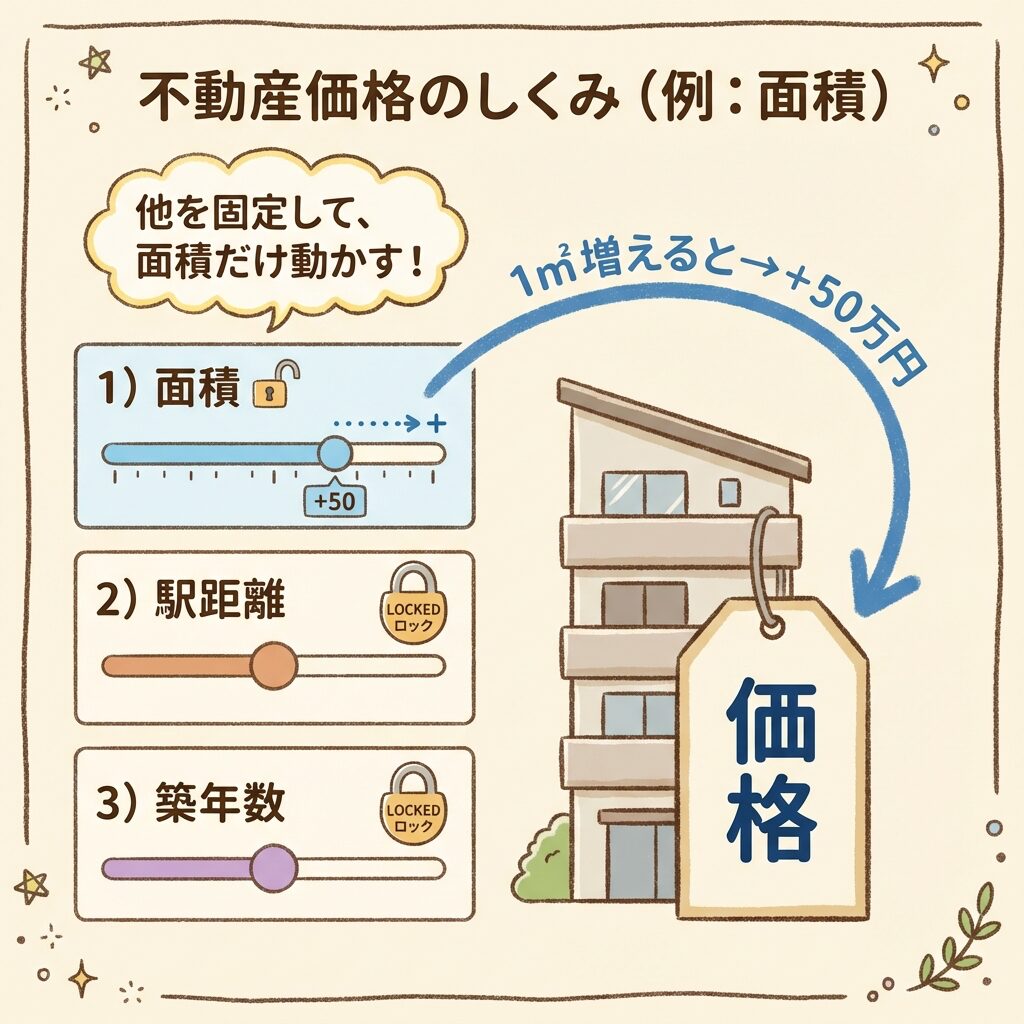
🔵 面積の偏回帰係数「+50」の意味
「駅徒歩分」と「築年数」を固定したとき、
面積が1㎡増えると、
価格が50万円上がる
つまり、「駅からの距離も築年数も同じマンション」を比べたとき、面積が1㎡広いと50万円高い、ということです。
🟠 駅徒歩分の偏回帰係数「−30」の意味
「面積」と「築年数」を固定したとき、
駅から1分遠くなると、
価格が30万円下がる
つまり、「面積も築年数も同じマンション」を比べたとき、駅から1分遠いと30万円安い、ということです。
🟣 築年数の偏回帰係数「−20」の意味
「面積」と「駅徒歩分」を固定したとき、
築年数が1年増えると、
価格が20万円下がる
つまり、「面積も駅距離も同じマンション」を比べたとき、1年古いと20万円安い、ということです。
偏回帰係数は、「他の条件が同じなら」という前提での影響度を表しています。これが「偏」という字の意味です。
🎚️ 「スライダー」でイメージしよう
偏回帰係数を理解するには、「スライダー」をイメージするとわかりやすいです。
🎮 ゲームの設定画面をイメージして
ゲームの設定画面には、「音量」「明るさ」「難易度」などのスライダーがありますよね。
重回帰分析も同じようにイメージできます。
【マンション価格を決めるスライダー】
| 面積 | 🔵━━━━●━━━━🔵 | 大きくすると価格UP |
| 駅距離 | 🟠━━━━●━━━━🟠 | 大きくすると価格DOWN |
| 築年数 | 🟣━━━━●━━━━🟣 | 大きくすると価格DOWN |
偏回帰係数を調べるときは、「1つのスライダーだけ動かして、他は固定する」のです。
「面積」のスライダーを1目盛り右に動かすと、価格メーターが50万円上がる
(ただし「駅距離」と「築年数」のスライダーは触らない!)
これが「他を固定したとき」の意味です。
🏃 具体例②:ダイエットで理解する
もう1つ、身近な例で考えてみましょう。
「1ヶ月で何キロ痩せるか」を予測する重回帰式があるとします。
(体重減少=kg、運動時間=時間/週、食事制限度=スコア、ストレス度=スコア)
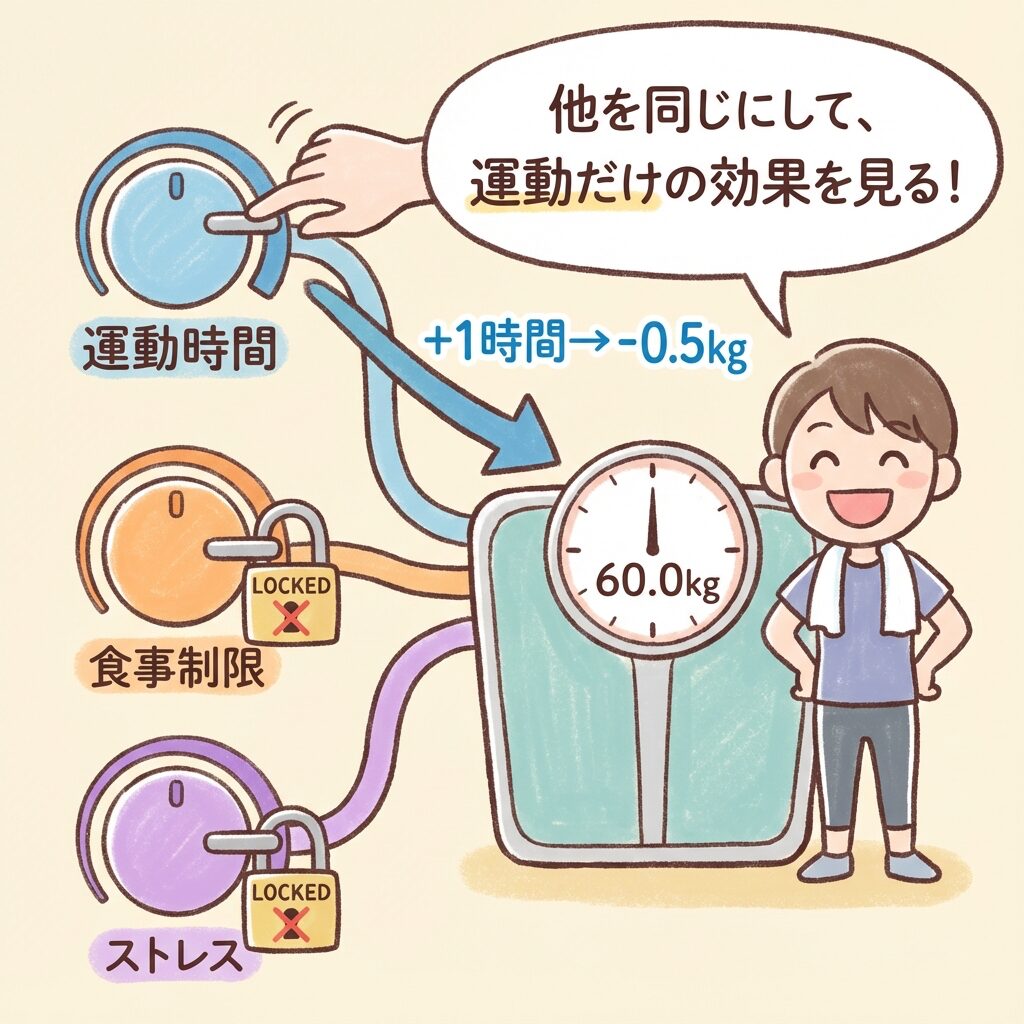
🔵 運動時間の偏回帰係数「+0.5」の意味
「食事制限度」と「ストレス度」が同じ人を比べたとき、
週の運動時間が1時間多いと、
1ヶ月で0.5kg多く痩せる
🟣 ストレス度の偏回帰係数「−0.1」の意味
「運動時間」と「食事制限度」が同じ人を比べたとき、
ストレス度が1ポイント高いと、
1ヶ月で0.1kg痩せにくい
「運動している人は痩せる」と言っても、運動している人はもともと食事にも気をつけているかもしれません。
偏回帰係数なら、「食事制限を同じにしても、運動だけで0.5kg痩せる」という純粋な運動の効果がわかるのです。
⚖️ 単回帰の「回帰係数」との違い
「偏回帰係数」と「回帰係数」は何が違うのでしょうか?
ここが重回帰分析を理解する上で最も重要なポイントです。
📝 具体例③:テストの点数で比較
「勉強時間」と「テストの点数」の関係を分析するとします。
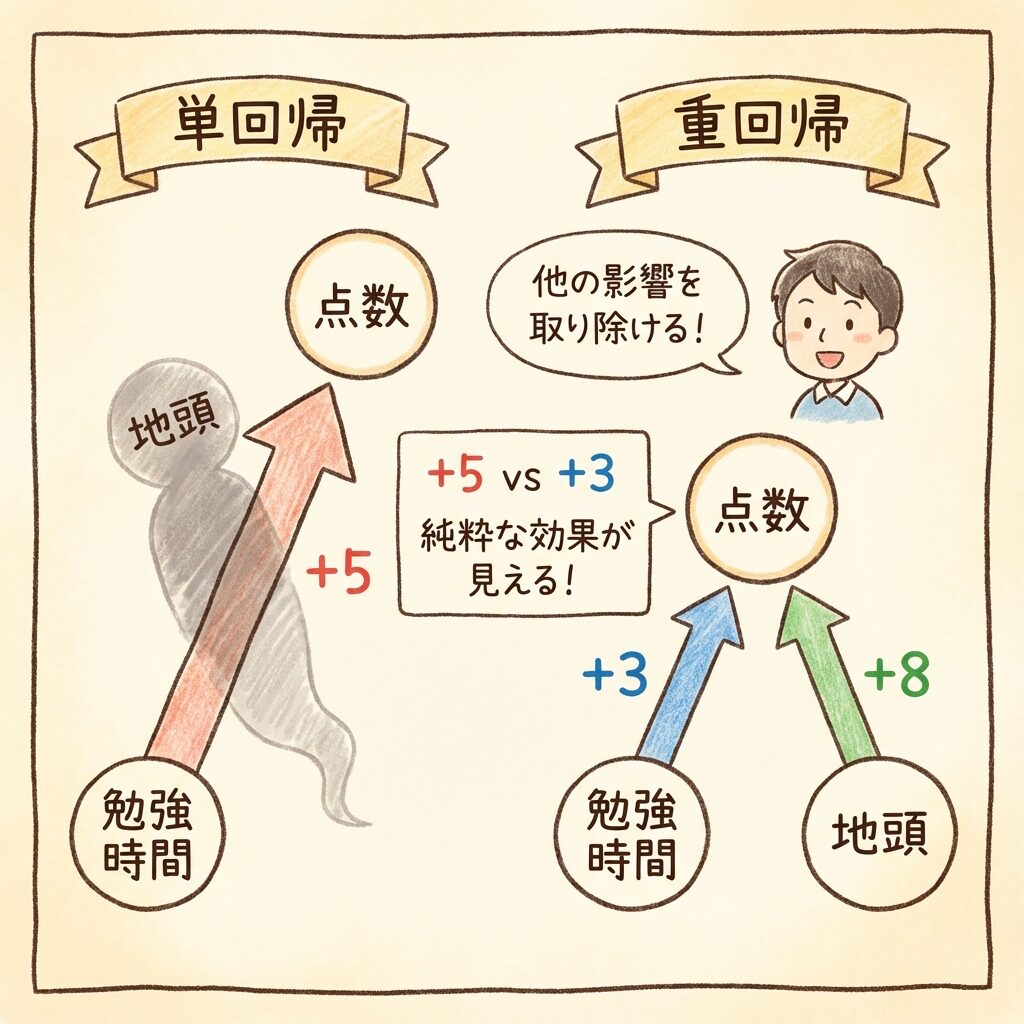
📘 単回帰分析の場合(勉強時間だけで予測)
→ 勉強時間が1時間増えると、点数が5点上がる
この「+5」が単回帰の回帰係数です。
でも、ちょっと待ってください。
勉強時間が長い人は、もともと地頭が良いかもしれません。
すると、「勉強時間の効果」と「地頭の効果」が混ざってしまっている可能性があります。
📗 重回帰分析の場合(勉強時間+地頭で予測)
→ 地頭が同じなら、勉強時間が1時間増えると、点数が3点上がる
この「+3」が偏回帰係数です。
🔍 比較してみよう
| 分析方法 | 勉強時間の係数 | 意味 |
|---|---|---|
| 単回帰(回帰係数) | +5 | 地頭の影響が混ざっている |
| 重回帰(偏回帰係数) | +3 | 地頭の影響を取り除いた純粋な効果 |
単回帰では「+5」だった勉強時間の効果が、重回帰では「+3」に減りました。
これは、単回帰の「+5」には地頭の効果が混ざっていたからです。
回帰係数(単回帰):他の要因の影響が混ざっている
偏回帰係数(重回帰):他の要因の影響を取り除いた「純粋な効果」
【統計学】「相関」と「回帰」の違いは?相関係数が高くても回帰分析をする理由 →
🔤 なぜ「偏」という字を使うのか?
「偏回帰係数」の「偏」という字、なんだか難しそうですよね。
でも、この「偏」には大切な意味があります。
📚 「偏」の意味
「偏」という字には「一部分だけを見る」「他を除外する」という意味があります。
「偏」がつく統計用語
- 偏差:平均を除外した「その値だけ」の散らばり
- 偏相関係数:他の変数の影響を除外した「2変数だけ」の相関
- 偏回帰係数:他の変数の影響を除外した「その変数だけ」の影響度
つまり「偏回帰係数」は、「他の変数の影響を除外(偏)して見た、回帰係数」という意味なのです。
🎯 偏回帰係数の大きさを比較できる?
「面積の係数が+50、駅距離の係数が−30だから、面積の方が影響が大きい!」
…と言いたくなりますが、ちょっと待ってください。
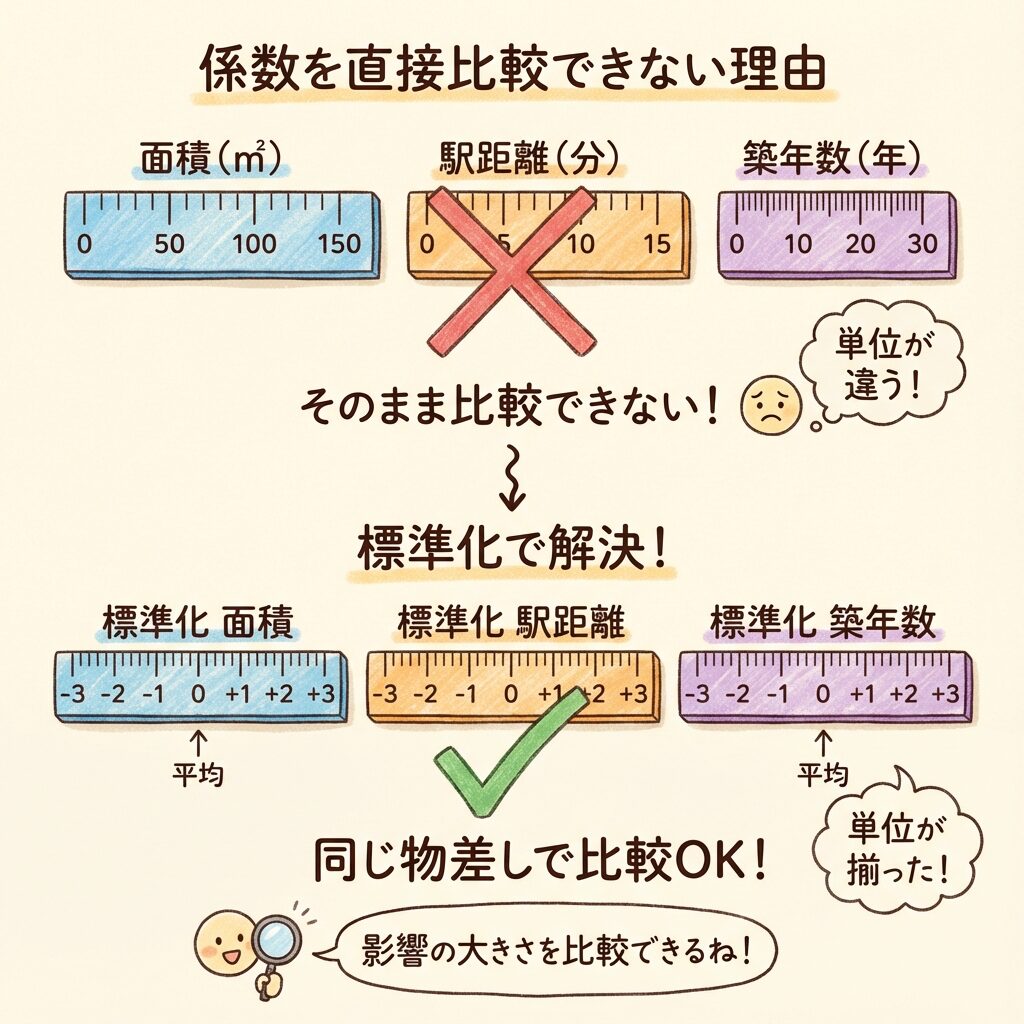
「面積」は㎡、「駅距離」は分、「築年数」は年と、単位がバラバラです。
単位が違う偏回帰係数を、そのまま比較して「どっちが影響が大きいか」を判断することはできません。
🔧 解決策:標準化偏回帰係数
「どの変数が一番影響力が大きいか」を比較したいときは、標準化偏回帰係数(標準偏回帰係数)を使います。
これは、すべての変数を「平均0、標準偏差1」に揃えてから計算した偏回帰係数です。
「面積」「駅距離」「築年数」を、同じ物差しで測り直すイメージです。
標準化すれば、「面積の標準化係数が0.6、駅距離が−0.3だから、面積の方が2倍影響力がある」と言えます。
📋 偏回帰係数のまとめ表
| 項目 | 内容 |
|---|---|
| 意味 | 他の変数を固定したとき、その変数が1単位増えると目的変数がどれだけ変化するか |
| 正の値 | その変数が増えると、目的変数も増える(正の影響) |
| 負の値 | その変数が増えると、目的変数は減る(負の影響) |
| ゼロに近い | その変数は目的変数にほとんど影響しない |
| 大きさの比較 | 単位が違う場合は標準化偏回帰係数を使う |
【統計学】説明変数(x)と目的変数(y)の違いとは?どっちが原因か迷わない覚え方 →
📋 まとめ
この記事では、偏回帰係数の意味を身近な例で解説しました。
- 偏回帰係数は「他の変数を固定したとき」の影響度
- イメージは「スライダー」:1つだけ動かして、他は固定
- 単回帰の回帰係数は他の影響が混ざっている
- 偏回帰係数は他の影響を取り除いた純粋な効果
- 大きさを比較するには標準化偏回帰係数を使う
偏回帰係数の「他を固定したとき」というポイントさえ押さえれば、重回帰分析はグッと理解しやすくなります。
次は、実際に偏回帰係数を計算する方法(正規方程式)を学びましょう。
📚 次に読むべき記事
実際に手を動かして偏回帰係数を計算する
重回帰モデル全体の有意性を検定する
偏回帰係数が統計的に有意かを判定する
【超入門】回帰分析とは?「未来を予測する」仕組みを小学生でもわかるように解説 →