※本記事にはプロモーション（広告）が含まれています。
- 「偏回帰係数って、どうやって計算するの？」
- 「正規方程式って何？なんだか難しそう…」
- 「切片β₀の求め方がわからない」
- 正規方程式の意味と導出の考え方
- 具体的な数値を使った計算手順
- 切片β₀と偏回帰係数β₁, β₂の求め方
- Excelや電卓で実際に計算する方法
前回の記事で、偏回帰係数の「意味」は理解できたと思います。
では、その偏回帰係数はどうやって計算するのでしょうか？
答えは「正規方程式」を解くことです。
名前は難しそうですが、やっていることは中学校で習った「連立方程式」を解くだけです。
この記事では、具体的な数値を使って、一緒に手を動かしながら計算していきましょう。
この記事の「偏回帰係数の意味」の節 ↓
まず意味から｜偏回帰係数とは「ほかを固定したときの影響」
正規方程式で求める偏回帰係数は、ほかの説明変数を一定にしたまま、その変数だけを1増やしたときに、y がどれだけ変わるかを表します。「偏」は「一部分だけ」という意味です。
例：中古マンションの価格（万円）を、広さ x₁（㎡）と築年数 x₂（年）で表した式が ŷ＝500＋30x₁−20x₂ だったとします。築年数が同じなら、広さが1㎡増えると価格は30万円上がり、広さが同じなら、築年数が1年古いと20万円下がる、と読みます。
| 単回帰の回帰係数 | 重回帰の偏回帰係数 | |
|---|---|---|
| 意味 | x が1増えたときの y の変化（ほかの要因の影響も混ざる） | ほかの変数を固定して、その変数だけを1増やしたときの変化 |
| 値 | ほかの要因と相関があると、その分まで背負って大きく・小さく出る | ほかの変数の影響を取り除いた値 |
注意したいのは、単位が違う偏回帰係数の大きさは、そのままでは比べられないことです。どの変数がより効いているかを比べるときは、データを標準化して求めた標準偏回帰係数を使います。
正規方程式とは？
まず、正規方程式が何なのかを理解しましょう。
一言でいうと
「残差の2乗和を最小にする」という条件から導かれる、偏回帰係数を求めるための連立方程式です。
「残差の2乗和を最小にする」という考え方は、単回帰分析の「最小二乗法」と同じです。
【統計学】最小二乗法とは？回帰直線を引く仕組みを「バネの力」で図解 →
なぜ「正規」という名前？
「正規方程式」の「正規」は、英語の "normal equation" の訳です。
ここでの "normal" は「正規分布」の意味ではなく、「直交する」という意味です。残差ベクトルが説明変数ベクトルに直交する、という幾何学的な性質から来ています。
名前の由来は気にしなくてOKです。「偏回帰係数を求めるための連立方程式」と覚えておけば十分です。
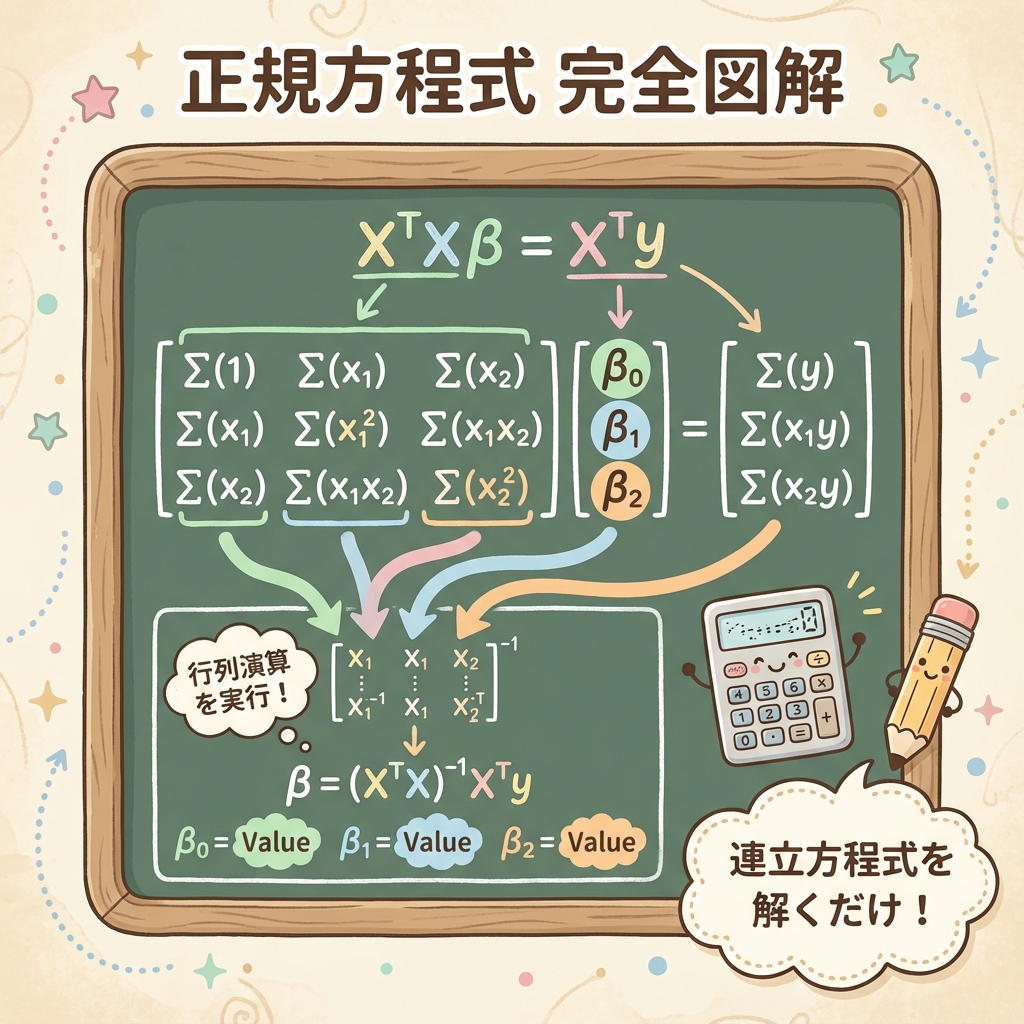
正規方程式の形
説明変数が2つ（x₁, x₂）の場合、正規方程式は以下の3本の連立方程式になります。
【正規方程式（説明変数2つの場合）】
① Σy = n·β₀ + β₁·Σx₁ + β₂·Σx₂
② Σx₁y = β₀·Σx₁ + β₁·Σx₁² + β₂·Σx₁x₂
③ Σx₂y = β₀·Σx₂ + β₁·Σx₁x₂ + β₂·Σx₂²
未知数はβ₀（切片）、β₁（x₁の偏回帰係数）、β₂（x₂の偏回帰係数）の3つです。
方程式が3本、未知数が3つなので、この連立方程式を解けばβ₀, β₁, β₂が求まります。
・Σy：yの合計
・Σx₁：x₁の合計
・Σx₁²：x₁の2乗の合計
・Σx₁x₂：x₁とx₂の積の合計
・Σx₁y：x₁とyの積の合計
・n：データの個数
残差と誤差の違いとは？式と計算例・残差プロットの見方を図解 →
具体例で計算してみよう
では、実際に数値を使って計算してみましょう。
例題：製品の強度を予測する
ある工場で、製品の強度（y）が、温度（x₁）と圧力（x₂）にどう影響されるかを調べました。
| No. | 温度 x₁ | 圧力 x₂ | 強度 y |
|---|---|---|---|
| 1 | 1 | 1 | 5 |
| 2 | 2 | 1 | 7 |
| 3 | 3 | 2 | 10 |
| 4 | 4 | 2 | 11 |
| 5 | 5 | 3 | 14 |
このデータから、重回帰式 y = β₀ + β₁x₁ + β₂x₂ の係数を求めます。
Step 1：必要な統計量を計算する
正規方程式に代入するために、まず以下の統計量を計算します。
| 統計量 | 計算 | 結果 |
|---|---|---|
| n | データの個数 | 5 |
| Σx₁ | 1+2+3+4+5 | 15 |
| Σx₂ | 1+1+2+2+3 | 9 |
| Σy | 5+7+10+11+14 | 47 |
| Σx₁² | 1+4+9+16+25 | 55 |
| Σx₂² | 1+1+4+4+9 | 19 |
| Σx₁x₂ | 1×1+2×1+3×2+4×2+5×3 | 32 |
| Σx₁y | 1×5+2×7+3×10+4×11+5×14 | 163 |
| Σx₂y | 1×5+1×7+2×10+2×11+3×14 | 96 |
Excelを使うなら、SUMPRODUCT関数が便利です。例えば Σx₁y は
=SUMPRODUCT(x₁の範囲, yの範囲) で一発計算できます。
第3回：平均値の奥深い世界 →
Step 2：正規方程式に代入する
計算した統計量を正規方程式に代入しましょう。
【正規方程式に代入】
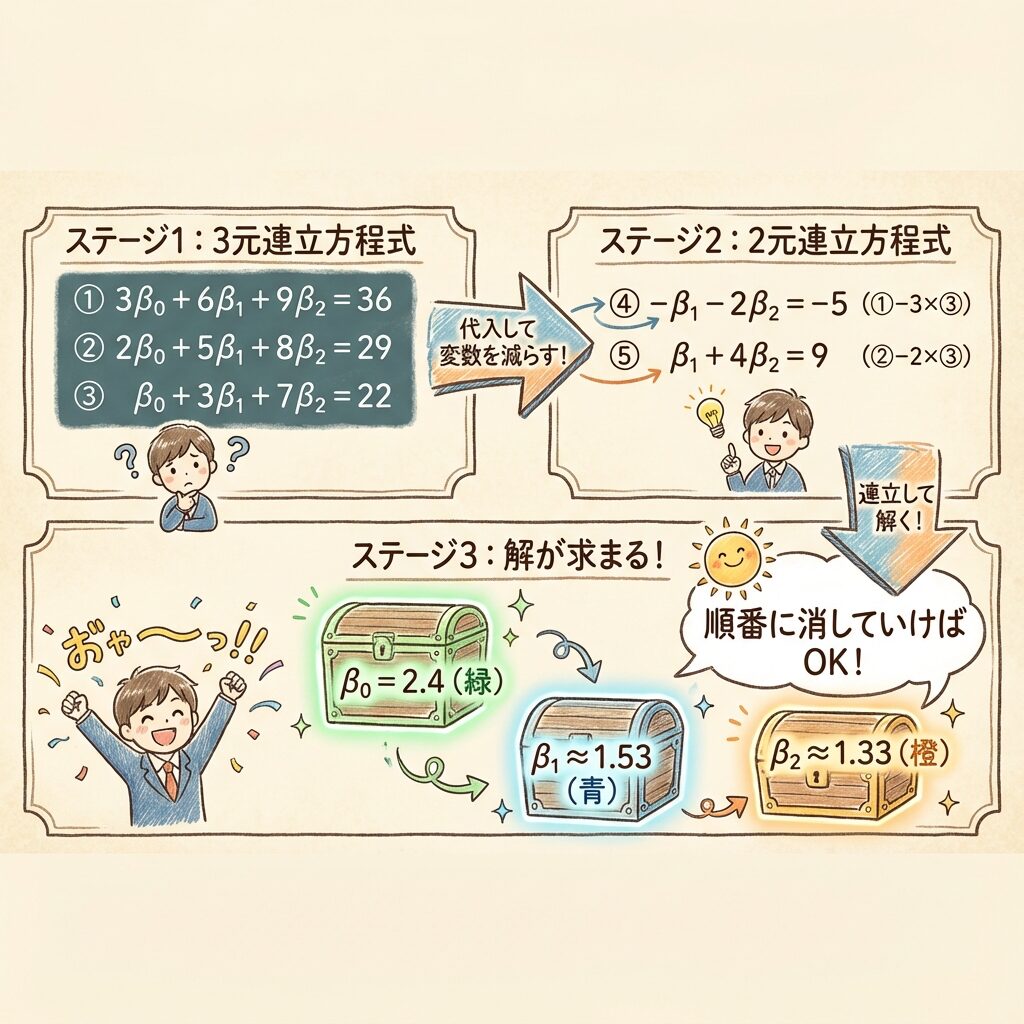
① 47 = 5β₀ + 15β₁ + 9β₂
② 163 = 15β₀ + 55β₁ + 32β₂
③ 96 = 9β₀ + 32β₁ + 19β₂
これで、β₀、β₁、β₂を求める3元1次連立方程式ができました。
Step 3：連立方程式を解く
連立方程式を解く方法はいくつかありますが、ここでは代入法で解いてみます。
Step 3-1：①式からβ₀を表す
①式を変形して、β₀を他の変数で表します。
5β₀ = 47 − 15β₁ − 9β₂
β₀ = 9.4 − 3β₁ − 1.8β₂
Step 3-2：②式と③式に代入してβ₀を消去
β₀ = 9.4 − 3β₁ − 1.8β₂ を②式と③式に代入します。
②式に代入：
163 = 141 − 45β₁ − 27β₂ + 55β₁ + 32β₂
163 = 141 + 10β₁ + 5β₂
22 = 10β₁ + 5β₂ ... ②'
③式に代入：
96 = 84.6 − 27β₁ − 16.2β₂ + 32β₁ + 19β₂
96 = 84.6 + 5β₁ + 2.8β₂
11.4 = 5β₁ + 2.8β₂ ... ③'
Step 3-3：2元連立方程式を解く
これで β₁ と β₂ の2元連立方程式になりました。
③' : 11.4 = 5β₁ + 2.8β₂
③'を2倍して②'から引きます。
22 − 22.8 = (10β₁ − 10β₁) + (5β₂ − 5.6β₂)
−0.8 = −0.6β₂
β₂ = 1.333...（約 4/3）
β₂ を②'に代入してβ₁を求めます。
22 = 10β₁ + 6.667
10β₁ = 15.333
β₁ = 1.533...（約 23/15）
最後に、β₁とβ₂を①'に代入してβ₀を求めます。
β₀ = 9.4 − 4.6 − 2.4
β₀ = 2.4
【統計学】「線形」とは何か？なぜ世界を直線で説明しようとするのか？ →
Step 4：結果をまとめる
これで、すべての係数が求まりました！
（小数点以下2桁に丸めた値）
係数の解釈
| 係数 | 値 | 解釈 |
|---|---|---|
| β₀（切片） | 2.4 | 温度=0、圧力=0のときの強度（ベースライン） |
| β₁（温度） | 1.53 | 圧力を固定して温度が1上がると、強度が1.53上がる |
| β₂（圧力） | 1.33 | 温度を固定して圧力が1上がると、強度が1.33上がる |
この記事の「偏回帰係数の意味」の節 ↓
検算してみよう
求めた式が正しいか、元のデータで検算してみましょう。
| No. | x₁ | x₂ | 実測値 y | 予測値 ŷ | 残差 |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 5 | 5.27 | −0.27 |
| 2 | 2 | 1 | 7 | 6.80 | +0.20 |
| 3 | 3 | 2 | 10 | 9.67 | +0.33 |
| 4 | 4 | 2 | 11 | 11.20 | −0.20 |
| 5 | 5 | 3 | 14 | 14.07 | −0.07 |
残差（実測値−予測値）が小さく、よく当てはまっていることがわかります。
残差の合計は理論上ゼロになるはずです（−0.27+0.20+0.33−0.20−0.07 ≈ 0）。これも正しく計算できた証拠です。
実務での計算方法
実際の仕事や研究では、手計算ではなくツールを使うのが一般的です。
Excelの場合
Excelの「データ分析」→「回帰分析」を使えば、一発で偏回帰係数が求まります。
- 「データ」タブ →「データ分析」→「回帰分析」を選択
- Y範囲（目的変数）とX範囲（説明変数）を指定
- 「OK」を押すと、係数・決定係数・検定結果などが一括出力
Pythonの場合
Pythonなら、scikit-learnやstatsmodelsライブラリで簡単に計算できます。
from sklearn.linear_model import LinearRegression
import numpy as np
X = np.array([[1,1], [2,1], [3,2], [4,2], [5,3]])
y = np.array([5, 7, 10, 11, 14])
model = LinearRegression()
model.fit(X, y)
print("切片:", model.intercept_) # β₀
print("係数:", model.coef_) # β₁, β₂
ツールを使うにしても、「何を計算しているのか」を理解していることが大切です。この記事で学んだ手計算の流れを知っていれば、ツールの出力結果も正しく解釈できます。
決定係数(R²)の正体｜「あてはまりの良さ」を視覚的に理解する →
まとめ
この記事では、重回帰分析で偏回帰係数を求める「正規方程式」を、具体的な数値例で解説しました。
- 正規方程式は、偏回帰係数を求めるための連立方程式
- 説明変数が2つなら、3本の連立方程式を解く
- 手順は①統計量を計算 → ②代入 → ③連立方程式を解く
- 実務ではExcelやPythonで簡単に計算できる
- 検算で残差の合計がゼロになるか確認
正規方程式の計算は、中学校の連立方程式と同じです。難しく考えず、順番に消去していけば必ず解けます。
次は、求めた重回帰式が「統計的に意味があるか」を検定する方法を学びましょう。
回帰分析の考え方を、楽しく復習したいときに向いています。回帰分析の考え方を、マンガで解説した本です（オーム社）。
「重回帰の正規方程式」の土台になる統計学を、本でじっくり学び直したいときに向いています。統計学を独学で学べるように書かれた入門書です（ダイヤモンド社、小島寛之 著）。
メーカーで電気設計と品質保証に携わってきた経験をもとに執筆しています。むずかしい専門用語をできるだけ使わず、はじめて学ぶ人がつまずかないように、図とたとえで説明することを大切にしています。
次に読むべき記事
この記事の内容がわかったら、重回帰分析の次のテーマに進みましょう。続けて読むと、現場でそのまま使える知識になります。
テーマ別に、もっと深く学ぶ
気になるところから読んでも大丈夫です。どの記事も、はじめて学ぶ人向けにやさしく書いています。
