😓「相関係数r=0.7って出たけど、本当に相関があるの?」
😓「サンプル数が少ないから、たまたまかもしれない…」
😓「フィッシャーのz変換って何?なぜ必要なの?」
こんな疑問、抱えていませんか?
相関係数を計算しただけでは、「それが信頼できる値なのか」がわかりません。サンプルから計算したrは、母集団の真の相関係数ρの「推定値」に過ぎないからです。
💡 結論ファースト
相関係数rの区間推定には「フィッシャーのz変換」を使います。rは-1〜+1の範囲に制限されて分布が歪むため、正規分布に従うzに変換してから信頼区間を計算し、最後にrに戻します。
📚 この記事でわかること
- なぜ相関係数rを直接区間推定できないのか
- フィッシャーのz変換の仕組みと公式
- 母相関係数ρの95%信頼区間の求め方(計算例付き)
- z変換表の使い方と逆変換の手順
📌 前提知識:この記事は相関係数の基礎を理解している方向けです。基礎から確認したい方は以下もどうぞ。
→ 「相関」と「回帰」の違いは?
→ 共分散とは?
目次
🤔 なぜ相関係数rを直接区間推定できないのか?
平均値の区間推定では、t分布を使って直接計算できました。しかし、相関係数rには厄介な性質があります。
📊 相関係数rの「壁」問題
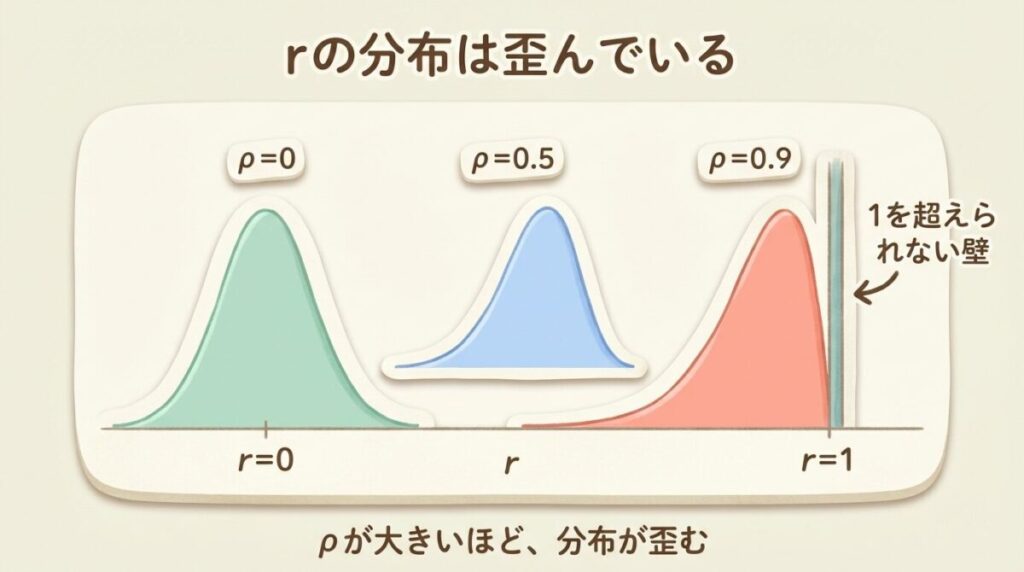
相関係数rは、定義上-1 ≤ r ≤ +1の範囲に制限されています。この「壁」があるせいで、rの標本分布は歪んでしまいます。
母相関係数ρの値による分布の変化:
ρ = 0 のとき
rの分布は
左右対称
ρ = 0.5 のとき
rの分布は
やや左に歪む
ρ = 0.9 のとき
rの分布は
大きく左に歪む
→ ρが1に近いほど、rは「+1の壁」に押されて分布が歪む
☕ イメージで理解
部屋の中でボールを投げる場面を想像してください。
部屋の真ん中で投げると、左右どちらにも自由に転がれます(対称)。
でも、壁際で投げると、壁にぶつかって跳ね返り、一方向にしか転がれません(歪み)。
相関係数rも同じです。±1という「壁」があるせいで、ρが大きいほど分布が歪むのです。
❌ 直接計算するとどうなる?
もしrの分布が歪んでいることを無視して、平均値のように「r ± 1.96 × SE」で信頼区間を計算すると…
⚠️ こんな問題が起きる
- 信頼区間が±1を超える:r = 0.9 のとき、上限が1.1になってしまう(あり得ない)
- 信頼区間が非対称になるべき場面で対称になる:誤った幅になる
- カバー率が95%にならない:本来の信頼度が保証されない
この問題を解決するために登場するのが、フィッシャーのz変換です。
🔄 フィッシャーのz変換とは?
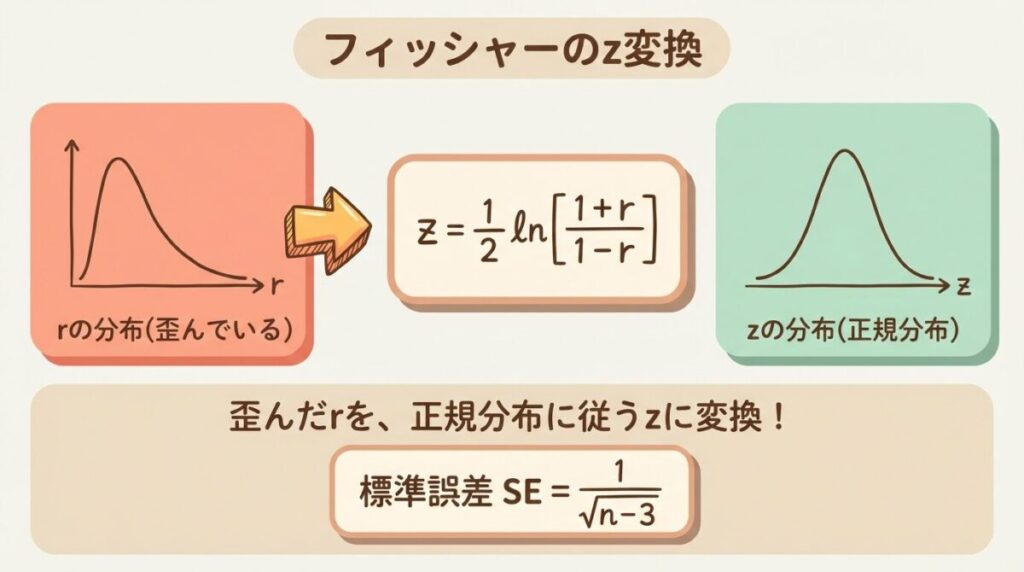
フィッシャーのz変換(Fisher's z-transformation)は、歪んだ相関係数rの分布を、正規分布に近づける変換です。統計学者ロナルド・フィッシャーが考案しました。
📐 z変換の公式
フィッシャーのz変換
z = 1/2 ln (1 + r/1 − r)
または z = tanh−1(r) (逆双曲線正接関数)
✨ z変換の3つの魔法
① 正規分布に近づく
歪んでいたrの分布が、
zに変換するとほぼ正規分布になる
② 分散が安定する
zの分散はρの値によらず
ほぼ一定(1/(n-3))になる
③ 範囲が無限大に広がる
rは-1〜+1だが、
zは-∞〜+∞の範囲を取れる
📊 zの標準誤差
zの標準誤差(SE)
SEz = 1/√(n − 3)
n = サンプルサイズ
この標準誤差は、rやρの値に関係なくサンプルサイズnだけで決まります。これがz変換の大きなメリットです。
📋 r → z 変換表(参考)
| r | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|---|---|---|---|---|---|---|---|---|
| z | 0.100 | 0.203 | 0.310 | 0.424 | 0.549 | 0.693 | 0.867 | 1.099 | 1.472 |
※ rが小さいときはr ≈ zですが、rが大きくなるほどzは急激に大きくなります。
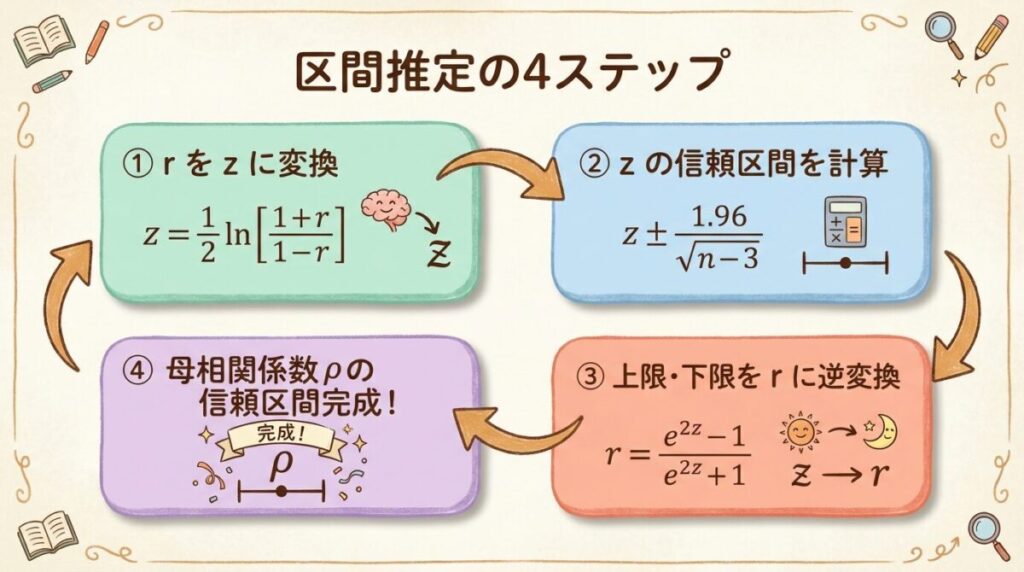
📝 区間推定の4ステップ
母相関係数ρの95%信頼区間を求める手順を、4ステップで解説します。
標本相関係数 r を z に変換
z = 1/2 ln (1 + r/1 − r)
z の95%信頼区間を計算
zL = z − 1.96 × 1/√(n−3) , zU = z + 1.96 × 1/√(n−3)
zL と zU を r に逆変換
r = e2z − 1/e2z + 1 または r = tanh(z)
母相関係数ρの信頼区間が完成!
rL ≤ ρ ≤ rU
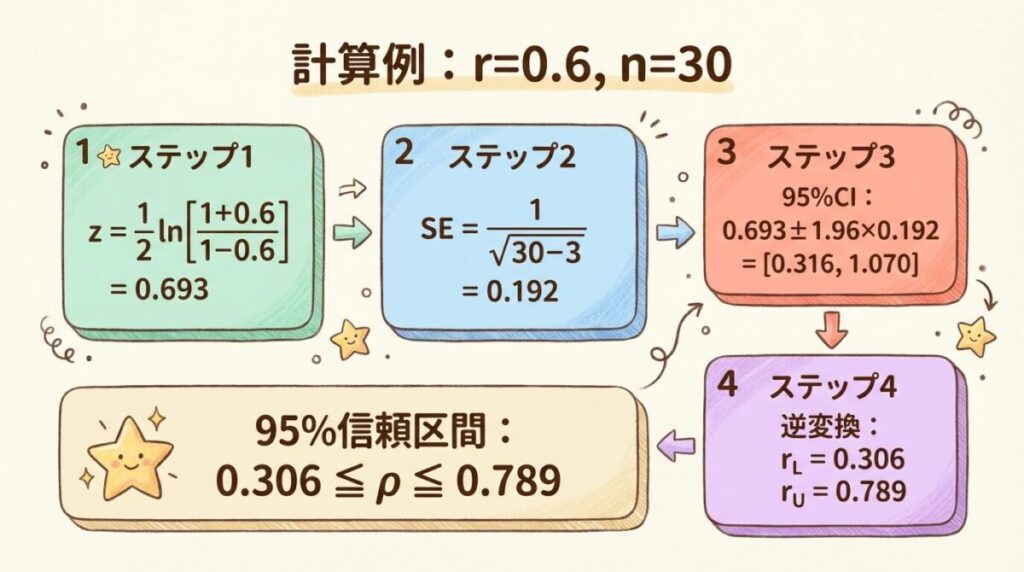
🧮 計算例:r = 0.6, n = 30
サンプルサイズ n = 30 で、標本相関係数 r = 0.6 が得られたとします。母相関係数ρの95%信頼区間を求めましょう。
Step 1:r を z に変換
z = 1/2 ln (1 + 0.6/1 − 0.6) = 1/2 ln (1.6/0.4) = 1/2 ln(4) = 1/2 × 1.386 = 0.693
Step 2:z の95%信頼区間を計算
SEz = 1/√(30 − 3) = 1/√27 = 1/5.196 = 0.192
zL = 0.693 − 1.96 × 0.192 = 0.693 − 0.377 = 0.316
zU = 0.693 + 1.96 × 0.192 = 0.693 + 0.377 = 1.070
Step 3:z を r に逆変換
rL = e2×0.316 − 1/e2×0.316 + 1 = e0.632 − 1/e0.632 + 1 = 1.881 − 1/1.881 + 1 = 0.881/2.881 = 0.306
rU = e2×1.070 − 1/e2×1.070 + 1 = e2.140 − 1/e2.140 + 1 = 8.499 − 1/8.499 + 1 = 7.499/9.499 = 0.789
Step 4:結論
🎯 母相関係数ρの95%信頼区間
0.306 ≤ ρ ≤ 0.789
📊 結果の解釈
「母集団における真の相関係数ρは、95%の確率で0.306〜0.789の範囲にある」と推定できます。
信頼区間に0が含まれていないので、「相関がない(ρ=0)」という仮説は棄却できます。つまり、母集団においても正の相関があると言えます。
⚠️ z変換を使うときの注意点
📏 サンプルサイズの目安
フィッシャーのz変換は近似的に正規分布に従うという性質を利用しています。そのため、サンプルサイズが小さすぎると精度が落ちます。
- n ≥ 25:一般的に推奨されるサンプルサイズ
- n ≥ 10:最低限必要なサンプルサイズ(精度は低下)
- n < 10:z変換の使用は推奨されない
🔢 信頼区間の非対称性
z変換を使った区間推定では、信頼区間がrに対して非対称になることがあります。これは正常な結果です。
上の計算例(r = 0.6)の場合:
下側の幅:0.6 − 0.306 = 0.294
上側の幅:0.789 − 0.6 = 0.189
→ 下側の方が広い(rが大きいほど上側が狭くなる傾向)
⚡ Excelでの計算方法
Excelの関数を使えば簡単に計算できます:
z変換:=FISHER(r)
逆変換:=FISHERINV(z)
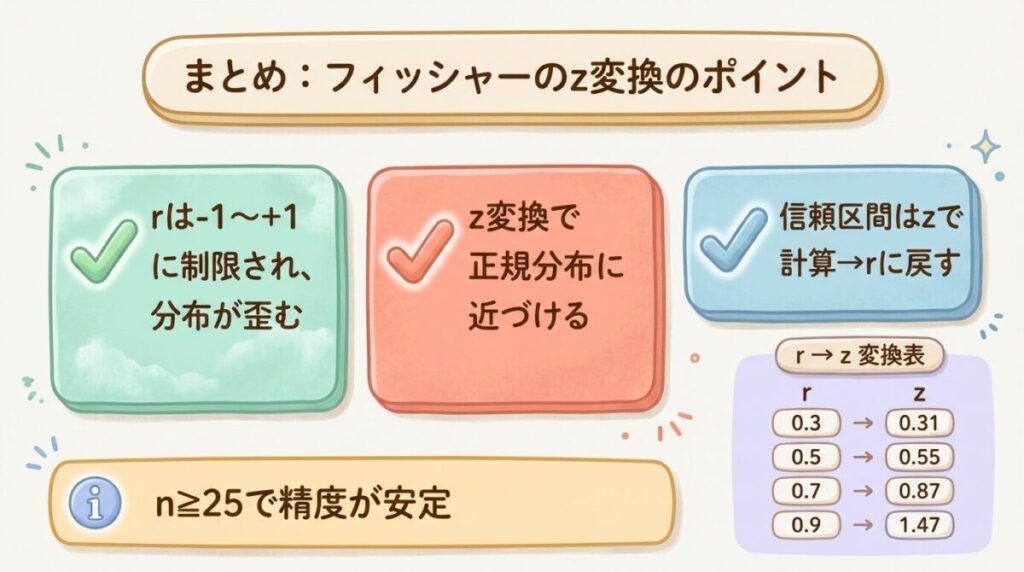
📌 まとめ
- 相関係数rは-1〜+1に制限されるため、分布が歪む
- フィッシャーのz変換で正規分布に近づけてから区間推定
- z変換の公式:z = (1/2) ln[(1+r)/(1-r)]
- zの標準誤差:SE = 1/√(n-3)
- zで信頼区間を計算→逆変換でrに戻す
- サンプルサイズはn ≥ 25が推奨
💡 試験対策のポイント
QC検定1級や統計検定では、z変換の公式と標準誤差の式を覚えておくことが重要です。計算問題では「z変換→信頼区間計算→逆変換」の4ステップを確実に実行できるようにしましょう。
最後までお読みいただきありがとうございました!
ご質問・ご感想は @shirasusolo までお気軽にどうぞ。
統計学のおすすめ書籍
統計学の「数式アレルギー」を治してくれた一冊
「Σ(シグマ)や ∫(インテグラル)を見ただけで眠くなる…」 そんな私を救ってくれたのが、小島寛之先生の『完全独習 統計学入門』です。
この本は、難しい記号を一切使いません。 「中学レベルの数学」と「日本語」だけで、検定や推定の本質を驚くほど分かりやすく解説してくれます。
「計算はソフトに任せるけど、統計の『こころ(意味)』だけはちゃんと理解したい」 そう願う学生やエンジニアにとって、これ以上の入門書はありません。
【QC2級】「どこが出るか」がひと目で分かる!最短合格へのバイブル
私がQC検定2級に合格した際、使い倒したのがこの一冊です。
この本の最大の特徴は、「各単元の平均配点(何点分出るか)」が明記されていること。 「ここは出るから集中」「ここは出ないから流す」という戦略が立てやすく、最短ルートで合格ラインを突破できます。
解説が分かりやすいため、私はさらに上の「QC1級」を受験する際にも、基礎の確認用として辞書代わりに使っていました。 迷ったらまずはこれを選んでおけば間違いありません。


