😰 こんな悩みはありませんか?
- 変圧器って、なんで電圧を変えられるの?
- 電磁誘導の法則がイメージできない…
- 巻数比と電圧比の関係がごちゃごちゃになる
- 理想変圧器って何が「理想」なの?
電験三種の勉強を始めたばかりの方なら、一度はこんな壁にぶつかったことがあるのではないでしょうか?
教科書を開いても数式と専門用語ばかりで、「結局どういう仕組みなの?」とモヤモヤしてしまいますよね。
でも、安心してください。変圧器の原理は、実はたった1つの法則を理解するだけで、驚くほどスッキリわかるんです。
✅ この記事の結論
変圧器は「磁束の変化で電圧が生まれる」という電磁誘導の法則を利用しています。
コイルの巻数を変えるだけで、電圧を自由に上げ下げできる。これが変圧器の正体です!
この記事では、変圧器の心臓部である「電磁誘導の法則」から、「巻数比と電圧・電流の関係」、そして「理想変圧器の条件」まで、イラストと具体例をたっぷり使って解説していきます。
目次
⚡ 電磁誘導の法則 ― すべてはここから始まる
変圧器を理解するための最重要キーワードが「電磁誘導」です。
これは19世紀にイギリスの科学者ファラデーが発見した法則で、電気と磁気の深い関係を表しています。
…と言われても、ピンとこないですよね。
大丈夫です。まずは「磁石とコイル」を使った簡単な実験をイメージしてみましょう。
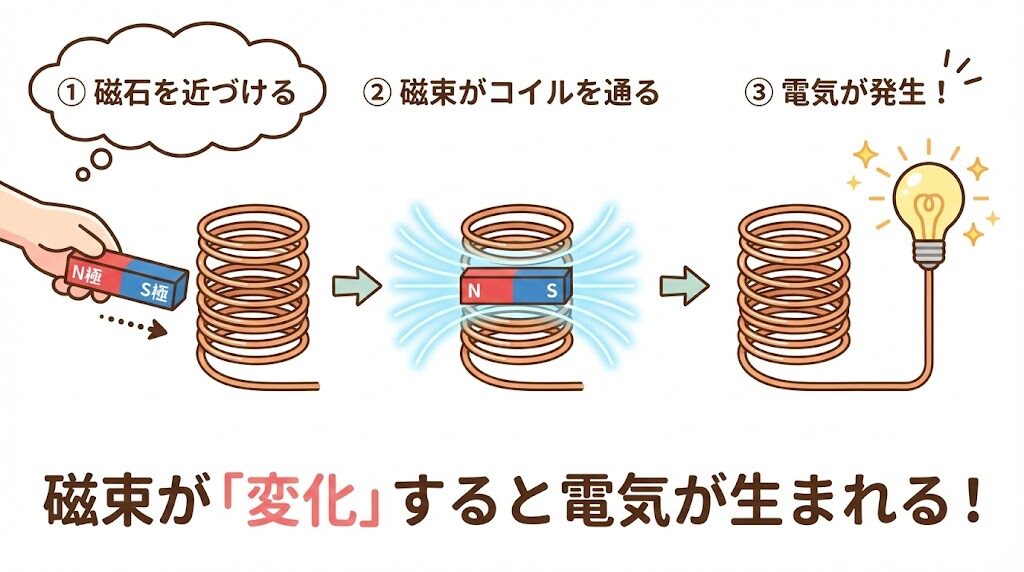
💡 電磁誘導を「磁石とコイル」でイメージしよう
上のイラストを見てください。やっていることはとてもシンプルです。
🧲 磁石とコイルの実験
① コイル(銅線をぐるぐる巻いたもの)を用意する
② そのコイルに磁石を近づけたり遠ざけたりする
③ すると、コイルに電圧(起電力)が発生する!
ここで超重要なポイントがあります。
それは「動かす」という部分です。
磁石をコイルの近くに置いたまま動かさなければ、何も起こりません。電気は生まれないのです。
でも、磁石を動かすと、コイルを貫く「磁束(じそく)」の量が変化します。
この「変化」こそが電気を生み出すトリガーなのです。
📌 電磁誘導のポイント
磁束が「変化」したときだけ、電気が発生する。
止まっていたら何も起こらない!
これを「ファラデーの電磁誘導の法則」と呼びます。公式で書くと次のようになります。
e = −N × (dΦ / dt)
e:誘導起電力[V] | N:コイルの巻数[回] | Φ:磁束[Wb] | t:時間[s]
数式が出てきましたが、怖がらなくて大丈夫です。
この式が言っていることは、たった2つだけです。
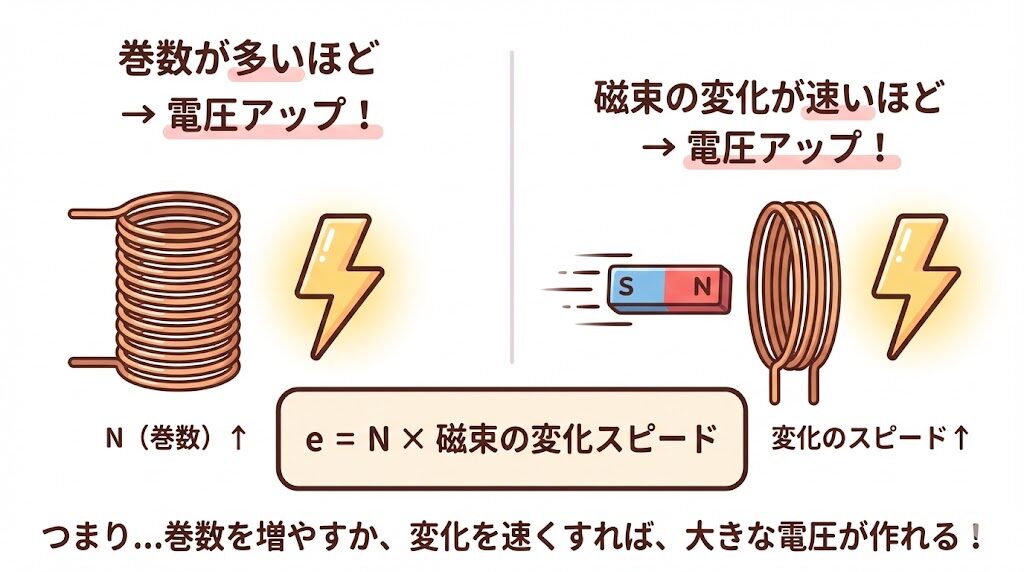
✅ ファラデーの法則が言っていること
① コイルの巻数が多いほど、大きな電圧が発生する
② 磁束の変化が速いほど、大きな電圧が発生する
変圧器は、まさにこの「巻数」を利用して電圧を変えているのです。
でも、ここで1つ疑問が出てきませんか?
「変圧器の中で、誰が磁石を動かしているの?」
実は、変圧器の中には動く磁石はありません。
その代わりに使っているのが「交流(こうりゅう)」です。
🔄 なぜ変圧器は「交流」じゃないと動かないの?
ここがとても大事なポイントです。
電気には「直流」と「交流」の2種類がありますよね。
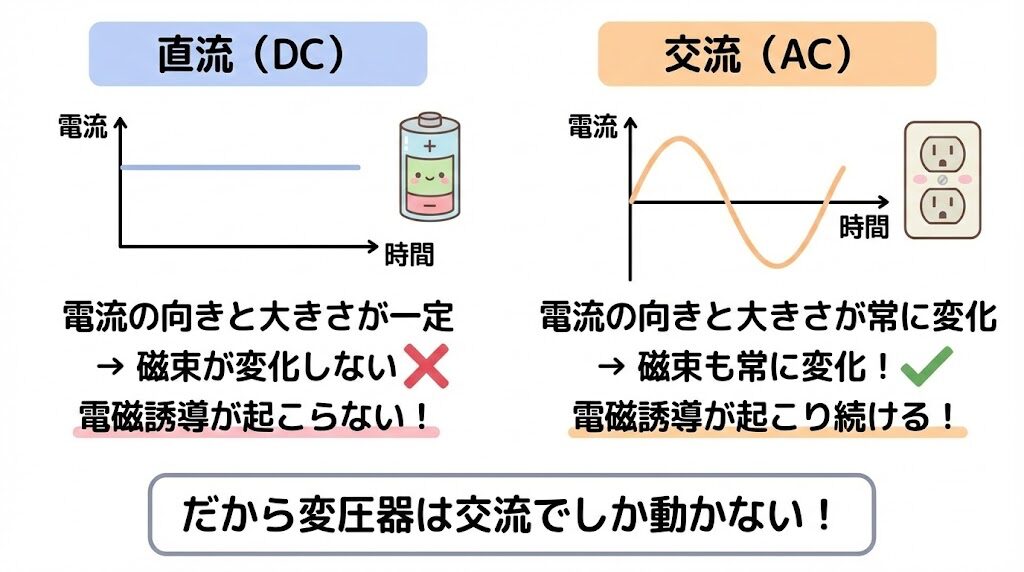
| 種類 | 電流の特徴 | 磁束 | 電磁誘導 |
|---|---|---|---|
| 直流(DC) | 向き・大きさが一定 | 変化しない | 起こらない ✕ |
| 交流(AC) | 向き・大きさが常に変化 | 常に変化 | 起こり続ける ◎ |
交流は、電流の向きと大きさがプラスとマイナスを行ったり来たりしています。
だから、磁石を動かさなくても、磁束が勝手に変化し続けるのです。
これが、変圧器が交流でしか動かない理由です。
⚠️ 試験でよく出るポイント!
「変圧器は交流専用」と覚えておきましょう。
直流では電磁誘導が起こらないので、変圧器は使えません。
🔌 一次コイルと二次コイルの関係
さて、電磁誘導の仕組みがわかったところで、いよいよ変圧器の中身を見ていきましょう。
変圧器の内部を見ると、鉄心(てっしん)という金属のかたまりに、2つのコイルが巻かれています。
この2つのコイルには、それぞれ名前と役割があります。
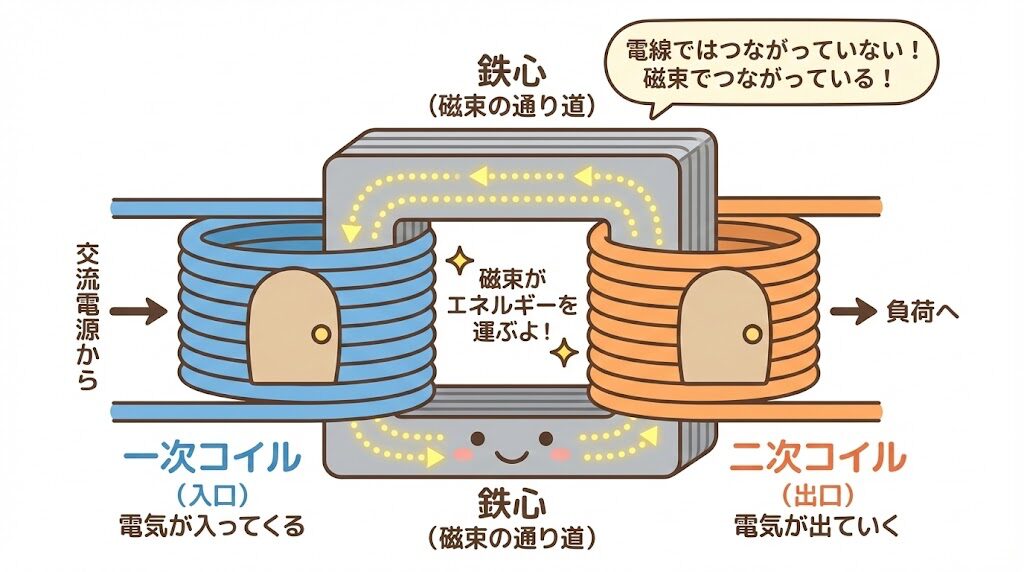
🚪 一次コイル = 電気の「入口」
一次コイルは、電源と接続される側です。家で例えると「玄関」のようなものですね。
電力会社から届いた交流電気が、ここから変圧器に入ってきます。
一次コイルに交流電流が流れると、鉄心に磁束が発生します。
そして交流なので、この磁束は常に変化し続けます。
🔋 二次コイル = 電気の「出口」
二次コイルは、変換された電圧を出力する側です。「裏口」や「出口」のイメージですね。
一次コイルで発生した磁束は、鉄心を通って二次コイルにも届きます。
磁束が変化しているので、二次コイルにも電磁誘導によって電圧が発生するのです!
🌉 超重要:2つのコイルは電線でつながっていない!
ここが変圧器の面白くて重要なポイントです。
✅ 一次コイルと二次コイルは電線では繋がっていません。
磁束という「見えないエネルギーの橋」を通じて、電力が受け渡されています。
これを「磁気結合(じきけつごう)」と呼びます。
電気的に絶縁されているのに、エネルギーだけは伝わる。
これが変圧器の大きな特徴であり、安全面でのメリットでもあります。
📏 巻数比と電圧比・電流比の関係
いよいよ変圧器の核心部分です!
「なぜ電圧を変えられるのか?」
その答えは、コイルの「巻数(まきすう)」にあります。
🔢 電圧比 = 巻数比
理想的な変圧器では、一次側と二次側の電圧の比は、コイルの巻数の比と等しくなります。
V₁ / V₂ = N₁ / N₂
V₁:一次電圧 | V₂:二次電圧 | N₁:一次巻数 | N₂:二次巻数
これを言葉で言い換えると、こうなります。
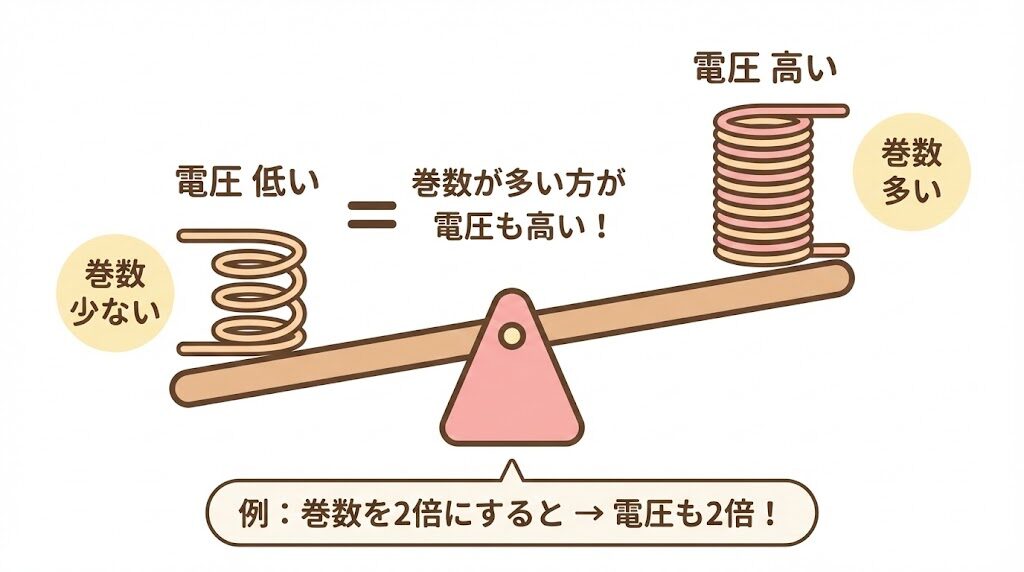
💡 覚え方はシンプル!
巻数が多い方が、電圧も高い。
シーソーをイメージすると覚えやすいですよ!
🧮 具体例で計算してみよう
実際に数字を使って計算してみましょう。
📝 計算例
【条件】
・一次電圧 V₁ = 6,600V
・一次巻数 N₁ = 3,300回
・二次巻数 N₂ = 100回
【計算】
V₂ = V₁ × (N₂ / N₁)
V₂ = 6,600 × (100 / 3,300)
V₂ = 6,600 × (1/33)
【答え】
V₂ = 200V
巻数を1/33にしたら、電圧も1/33になりました!
このように、巻数の比率を変えるだけで、好きな電圧を作り出せるのです。
⚖️ 電流比は巻数比の「逆」になる
電圧の次は電流です。ここで覚えておいてほしいことがあります。
それは、電流比は電圧比の「逆」になるということです。
I₁ / I₂ = N₂ / N₁
電流比は巻数比の逆数になる
なぜ逆になるのでしょうか?
それは、エネルギー(電力)が保存されるからです。
水道で例えてみましょう。
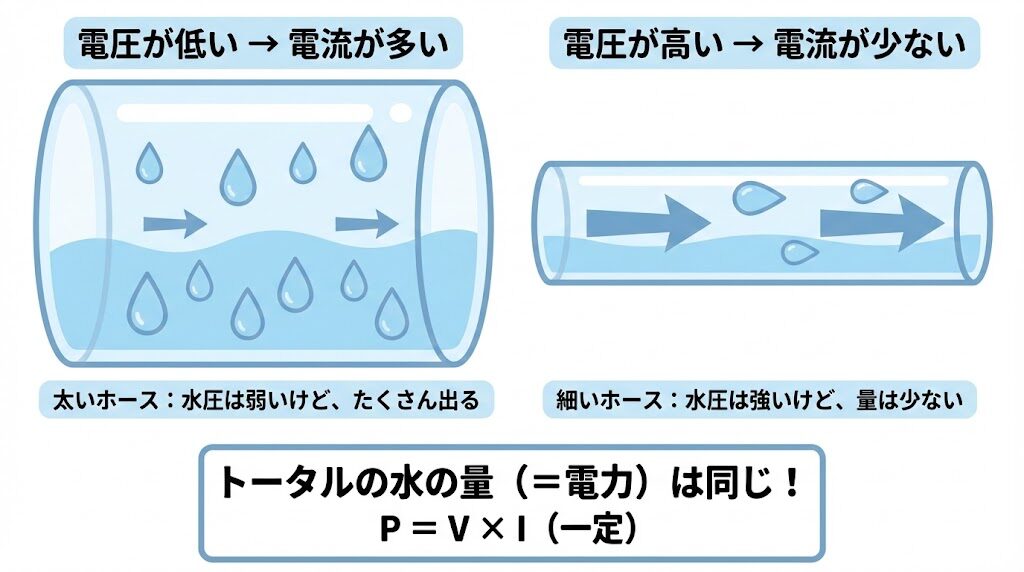
🚿 水道で例えると…
ホースの先を細くすると、水圧(=電圧)は上がりますよね。
でも、出てくる水の量(=電流)は減ります。
逆に、ホースを太くすると、水圧は下がるけど、たくさんの水が出ます。
トータルの水の量(=電力)は変わらないのです。
変圧器も同じです。
✅ 電力保存の法則
電圧を上げれば → 電流は減る
電圧を下げれば → 電流は増える
でも、電力(P = V × I)は変わらない!
📊 電圧比・電流比・電力の関係まとめ
| 項目 | 関係式 | 覚え方 |
|---|---|---|
| 電圧比 | V₁ : V₂ = N₁ : N₂ | 巻数が多い方が電圧も高い |
| 電流比 | I₁ : I₂ = N₂ : N₁ | 巻数が多い方が電流は小さい |
| 電力 | P₁ = P₂(理想時) | 入力と出力は等しい |
✨ 理想変圧器の条件
ここまで説明してきた「電圧比 = 巻数比」という関係は、実は「理想変圧器」を前提としています。
「理想」って何が理想なの?と思いますよね。
簡単にいうと、「損失が一切ない、完璧な変圧器」のことです。
理想変圧器が満たすべき条件は、次の4つです。
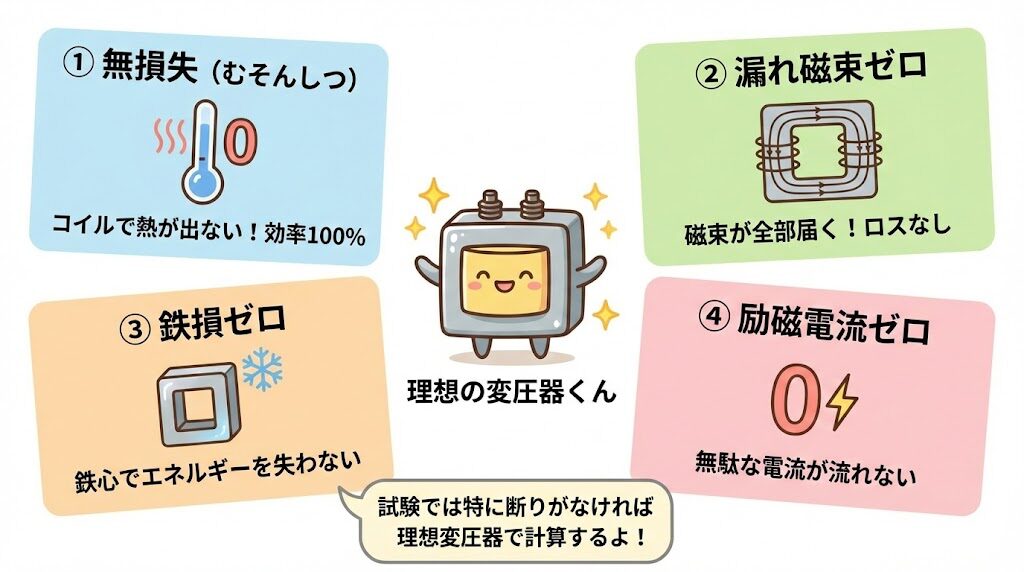
🎯 理想変圧器の4つの条件
① 無損失
コイルの抵抗がゼロ。
電流が流れても熱(銅損)が発生しない。
② 漏れ磁束ゼロ
一次コイルで作った磁束が、100%二次コイルに届く。
③ 鉄損ゼロ
鉄心でのヒステリシス損や渦電流損が発生しない。
④ 励磁電流ゼロ
鉄心を磁化するための電流が不要。透磁率が無限大。
現実の変圧器では、これらの条件を完全に満たすことは不可能です。
でも、最新の技術により、効率98〜99%以上を達成する変圧器も珍しくありません。ほぼ理想に近いと言えますね。
📝 試験対策のポイント
電験三種の試験問題では、特に断りがない限り「理想変圧器」として計算します。
「損失を考慮せよ」「効率は〇〇%とする」などの指示がある場合のみ、損失を加味した計算が必要になります。
📝 まとめ:変圧器の基本原理
☕ 今日のおさらい
- 電磁誘導の法則:磁束の「変化」がコイルに電圧を発生させる
- 交流が必要な理由:直流では磁束が変化しないから
- 一次コイル:電源に接続し、磁束を作り出す(入口)
- 二次コイル:磁束を受け取り、電圧を出力する(出口)
- 電圧比 = 巻数比:巻数が多い方が電圧も高い
- 電流比 = 巻数比の逆:電圧が上がれば電流は減る
- 理想変圧器の4条件:無損失・漏れ磁束ゼロ・鉄損ゼロ・励磁電流ゼロ
変圧器は、発電所から家庭まで電気を届ける「縁の下の力持ち」です。
今回学んだ基本原理は、今後学ぶ「変圧器の等価回路」「三相変圧器」「電圧変動率」など、すべての土台になります。
まずはこの記事の内容をしっかり理解して、次のステップに進んでいきましょう!
💪
変圧器の基本原理、お疲れさまでした!
この調子で一歩ずつ進んでいきましょう。応援しています!
