😰 こんな悩みはありませんか?
- 等価回路って何?なんで必要なの?
- 一次換算と二次換算の違いがわからない…
- 励磁電流とか鉄損電流とか、用語が多すぎる
- %Z(パーセントインピーダンス)の意味が謎
変圧器の勉強で、多くの人がつまずくのが「等価回路」です。
でも、安心してください。等価回路は「複雑な変圧器を、シンプルな回路に置き換える」ためのツールです。
一度理解してしまえば、計算問題がグッとラクになりますよ。
✅ この記事の結論
等価回路とは、変圧器の「損失」や「電圧降下」を抵抗とコイルで表した回路図。
すべてを一次側(または二次側)に換算すれば、普通の直列回路として計算できる!
目次
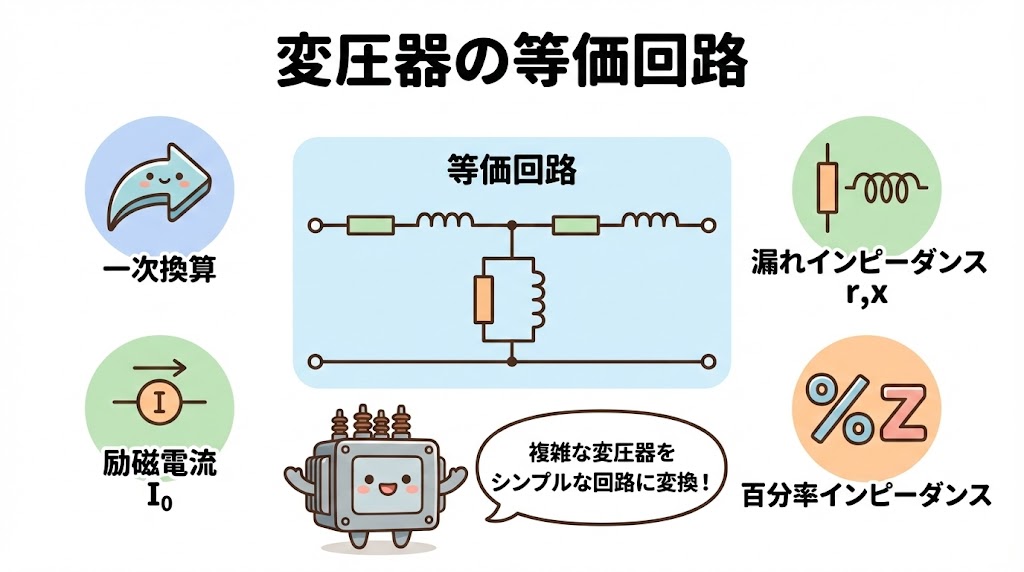
🤔 そもそも「等価回路」とは何か?
まず、「等価回路」という言葉の意味から確認しましょう。
等価とは「同じ価値」という意味です。つまり等価回路とは、「実際の変圧器と同じ動きをする、シンプルな回路」のことです。
💡 なぜ等価回路が必要なのか?
前回までの記事では、「理想変圧器」を前提に計算してきました。
でも、現実の変圧器には理想にはない「ロス」がいくつもあります。
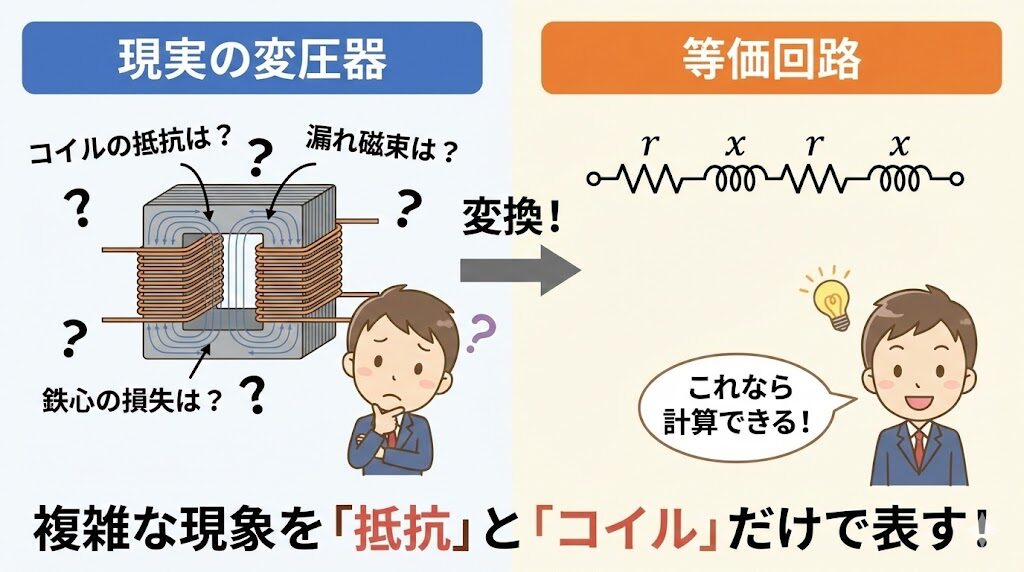
⚠️ 現実の変圧器にある「ロス」
① コイルの抵抗:銅線には抵抗があり、電流が流れると熱が出る
② 漏れ磁束:一次コイルで作った磁束が100%二次に届かない
③ 鉄心の損失:鉄心を磁化するのにエネルギーを使う
④ 励磁電流:鉄心を磁化するための電流が必要
これらの「ロス」を、抵抗(r)とリアクタンス(x)という部品で表したのが等価回路です。
🏠 家の設計図で例えると…
実際の家は複雑ですが、設計図(間取り図)があれば簡単に理解できますよね。
等価回路は、変圧器の「設計図」のようなもの。
複雑な現象を、シンプルな図で表しているのです。
📐 変圧器の等価回路(T型等価回路)
それでは、変圧器の等価回路を見ていきましょう。
最も基本的な形は「T型等価回路」と呼ばれます。アルファベットの「T」の形に似ているからです。

🔍 等価回路の各パーツを理解しよう
T型等価回路は、大きく3つのブロックに分かれています。
| ブロック | 記号 | 意味 |
|---|---|---|
| 一次側 | r₁、x₁ | 一次コイルの抵抗と漏れリアクタンス |
| 励磁回路 | g₀、b₀ | 鉄心の損失と磁化に必要な電流 |
| 二次側 | r₂、x₂ | 二次コイルの抵抗と漏れリアクタンス |
🔵 一次側のパーツ(r₁、x₁)
一次コイルには、2つの「抵抗」があります。
r₁(一次抵抗)
銅線の電気抵抗。
電流が流れると熱が発生する(銅損の原因)。
x₁(一次漏れリアクタンス)
漏れ磁束による影響。
二次側に届かなかった磁束が原因。
🟢 励磁回路のパーツ(g₀、b₀、I₀)
T型等価回路の「縦の部分」が励磁回路です。ここが理想変圧器にはない、現実の変圧器特有の部分です。
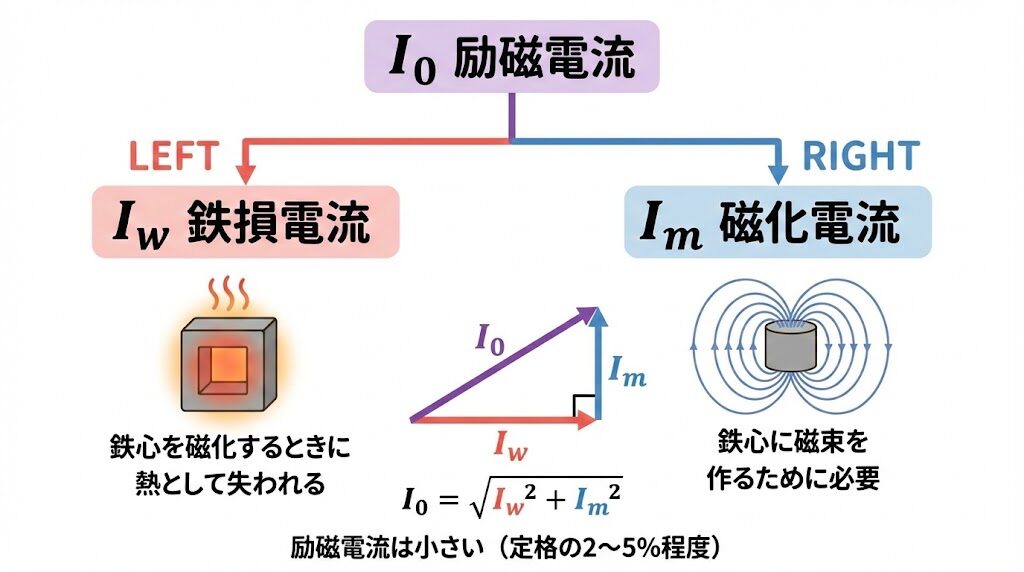
励磁回路には、励磁電流 I₀という特別な電流が流れています。
この励磁電流は、2つの成分に分けられます。
Iw(鉄損電流)
鉄心で発生する損失に対応する電流。
ヒステリシス損と渦電流損の原因。
電圧と同相(位相が同じ)。
Im(磁化電流)
鉄心に磁束を作るための電流。
損失にはならないが、必要な電流。
電圧より90°遅れ。
I₀ = √(Iw² + Im²)
励磁電流は、鉄損電流と磁化電流のベクトル合成
💡 励磁電流のポイント
・励磁電流 I₀ は非常に小さい(定格電流の2〜5%程度)
・無負荷のとき、ほぼ励磁電流だけが流れる
・だから「無負荷試験」で励磁電流を測定できる
🟠 二次側のパーツ(r₂、x₂)
二次側も一次側と同じ構成です。
r₂(二次抵抗)
二次コイルの銅線の電気抵抗。
x₂(二次漏れリアクタンス)
二次側の漏れ磁束による影響。
🔄 一次側換算と二次側換算
T型等価回路には、一次側と二次側の両方にパーツがあります。
でも、このままだと計算が面倒ですよね。一次側は一次側、二次側は二次側…と分けて考えなければなりません。
そこで使うのが「換算」というテクニックです。
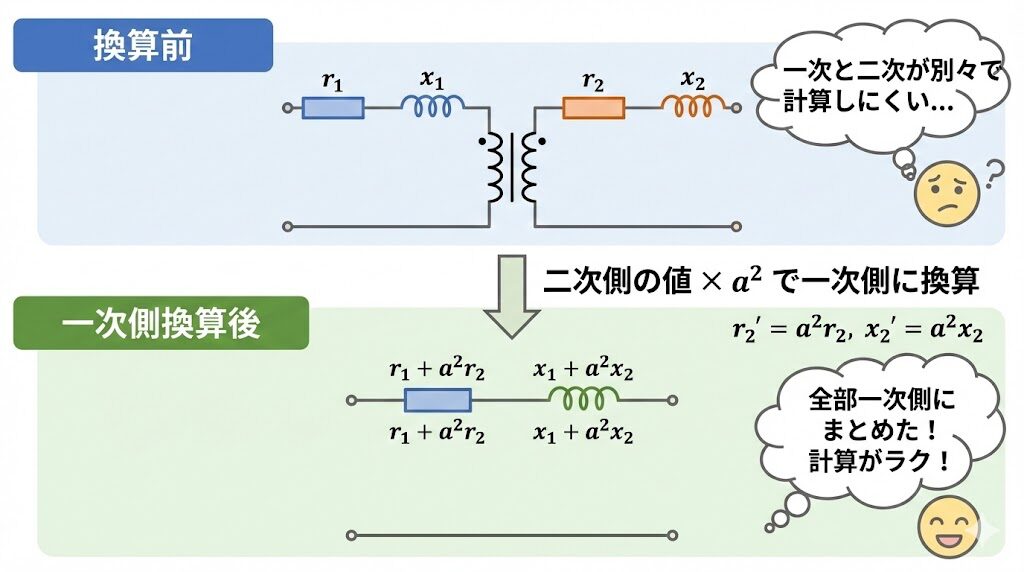
📍 換算とは? ― すべてを「片側」にまとめる
換算とは、二次側のパーツを一次側に移動させる(またはその逆)ことです。
すべてを片側にまとめると、普通の直列回路として計算できるようになります。
💴 お金で例えると…
1ドル = 150円 のとき、10ドルを円に換算すると 1,500円 ですよね。
変圧器の換算も同じ。
「二次側の言葉(電圧・電流・インピーダンス)」を
「一次側の言葉」に翻訳するのです。
📐 一次側換算の公式
前回学んだ「巻数比 a」を使って換算します。
r₂' = a² × r₂
x₂' = a² × x₂
V₂' = a × V₂
I₂' = I₂ / a
「'」(ダッシュ)は「換算後」を表す記号
インピーダンス(r、x)はa²倍、電圧はa倍、電流は1/a倍。
前回の記事で学んだ公式そのままですね!
📐 二次側換算の公式
逆に、一次側を二次側に換算することもできます。
r₁' = r₁ / a²
x₁' = x₁ / a²
V₁' = V₁ / a
I₁' = I₁ × a
一次側換算の逆。割り算になる。
✅ 換算のポイント
・一次側換算:二次側の値に a² や a をかける
・二次側換算:一次側の値を a² や a で割る
・どちらに換算するかは問題によって使い分ける
⚡ 簡易等価回路(L型等価回路)
実際の試験では、T型等価回路をさらに簡略化した「簡易等価回路」がよく使われます。
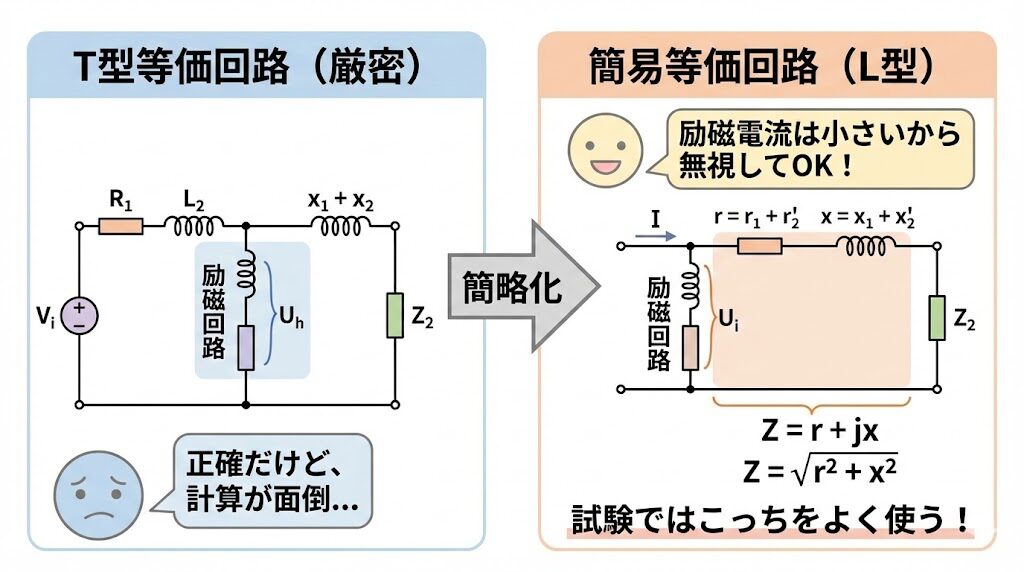
🎯 なぜ簡易化できる?
励磁電流 I₀ は定格電流の2〜5%程度と非常に小さいです。
だから、励磁回路の位置を入力側に移動しても、計算結果にほとんど影響しません。
さらに、一次側と二次側の抵抗・リアクタンスを1つにまとめることで、計算がグッとラクになります。
r = r₁ + a²r₂
x = x₁ + a²x₂
Z = √(r² + x²)
r:合成抵抗 | x:合成リアクタンス | Z:合成インピーダンス
この合成インピーダンス Z が、変圧器の「内部での電圧降下」を決めます。
📊 百分率インピーダンス(%Z)
変圧器のカタログや問題文でよく見かける「%Z」という値。
これは、インピーダンスを「パーセント」で表したものです。
🤔 なぜパーセントで表す?
変圧器には様々な容量があります。100kVAの変圧器と10MVAの変圧器では、インピーダンスの「Ω(オーム)」の値が全然違います。
でも、%Zで表せば、容量が違う変圧器でも比較できるのです。
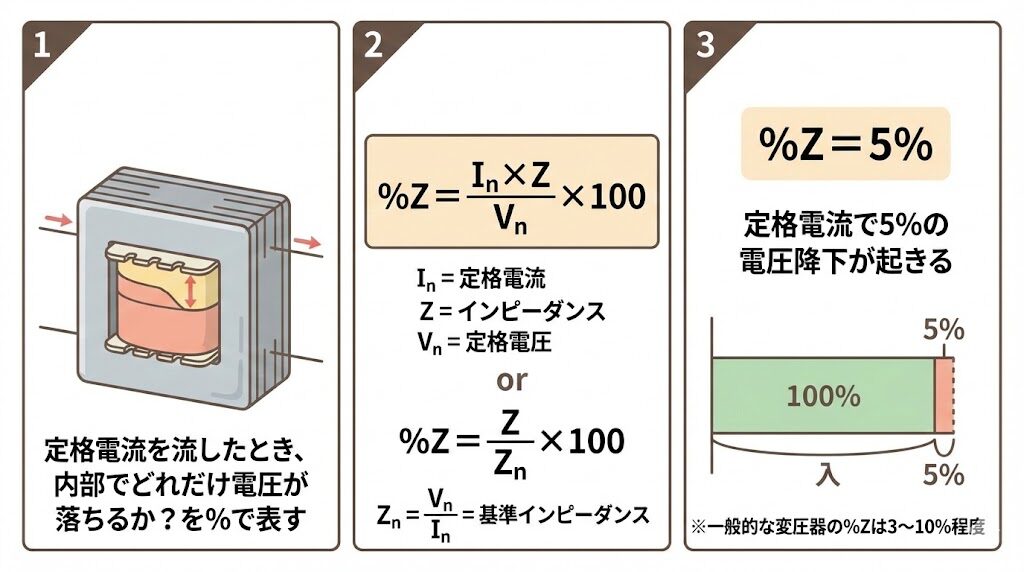
🎯 %Zの意味を一言で
「定格電流を流したとき、内部で何%の電圧降下が起きるか」
%Z = 5% なら、定格電流で5%の電圧が内部で失われるということ。
📐 %Zの公式
%Z = (Iₙ × Z / Vₙ) × 100
Iₙ:定格電流 | Z:インピーダンス[Ω] | Vₙ:定格電圧
同様に、抵抗とリアクタンスもパーセントで表せます。
%R = (Iₙ × r / Vₙ) × 100 (百分率抵抗降下)
%X = (Iₙ × x / Vₙ) × 100 (百分率リアクタンス降下)
%Z = √(%R² + %X²) の関係がある
🧮 %Zの計算例
📝 例題
【条件】
・定格容量:100kVA
・定格電圧:6,600V / 200V
・一次換算インピーダンス:Z = 21.8Ω
【計算】
① 定格電流を求める
Iₙ = 100,000 / 6,600 = 15.15A
② %Zを求める
%Z = (15.15 × 21.8 / 6,600) × 100
%Z = (330.3 / 6,600) × 100
%Z = 5%
この変圧器は、定格電流で5%の電圧降下が起きることがわかりました。
✅ %Zのポイント
・一般的な変圧器の%Zは3〜10%程度
・%Zが小さいほど電圧降下が少ない(良い変圧器)
・%Zが小さすぎると短絡電流が大きくなる(危険)
・並行運転では%Zが同じ変圧器を使う
📊 等価回路の公式まとめ
| 項目 | 記号・公式 | 意味 |
|---|---|---|
| 一次換算抵抗 | r = r₁ + a²r₂ | 銅損の原因 |
| 一次換算リアクタンス | x = x₁ + a²x₂ | 漏れ磁束の影響 |
| 合成インピーダンス | Z = √(r² + x²) | 電圧降下の原因 |
| 励磁電流 | I₀ = √(Iw² + Im²) | 鉄心を磁化する電流 |
| %Z | (Iₙ × Z / Vₙ) × 100 | 定格時の電圧降下率 |
📝 まとめ:等価回路とベクトル図
☕ 今日のおさらい
- 等価回路:変圧器の損失・電圧降下を抵抗とコイルで表した回路
- T型等価回路:一次側 + 励磁回路 + 二次側の3ブロック
- 励磁電流 I₀:鉄損電流 Iw と磁化電流 Im の合成
- 一次換算:二次側の値に a² をかけて一次側にまとめる
- 簡易等価回路:励磁回路を省略し、計算を簡単にする
- %Z:定格電流での電圧降下率(一般的に3〜10%)
等価回路が描ければ、変圧器の電圧変動率や短絡電流の計算ができるようになります。
次の記事では、等価回路を使って「損失と効率」を計算していきましょう!
💪
等価回路、マスターできましたか?
「複雑→シンプル」に変換するのが等価回路の役割です!