管理図のA2・D3・D4の意味｜d2から導く理由と係数の検算表

※本記事にはプロモーション（広告）が含まれています。

結論：係数は「3σ計算を簡略化する」ための変換値

いきなり結論からお伝えします。A2・D3・D4の正体は、「本来は3σで計算すべきところを、R̄（範囲の平均）だけで計算できるようにした変換係数」です。

つまり、こういうことです。

この「なぜ」がわかると、係数表がただの数字の羅列ではなく、意味のある値として見えてきます。

係数の値を自分で検算する｜n＝2〜10の表と数値例

導いた式が本当に係数表と同じになるかを、d2・d3 から計算して確かめます。表の A2・D3・D4 は、管理図の係数表に一般に載っている値です（d2・d3 を丸める前の値から計算しているため、丸めた d2・d3 で計算すると n＝2 などで3けた目が1ずれることがあります）。

n＝5で D4 を検算する

n＝5 のとき、d2＝2.326、d3＝0.864 です。d3÷d2＝0.864÷2.326＝0.3715。これを3倍すると1.114。D4＝1＋1.114＝2.114 で、係数表の値と一致します。D3＝1−1.114＝−0.114 とマイナスになるので、表では「－」（下限を設けない）です。

数値例：X̿＝50.0、R̄＝4.0、n＝5 の管理限界

たとえば A2 の 0.577 は、「平均値の3σの幅は、R̄ の0.577倍」という意味です。n が大きいほど平均値のばらつきが小さくなるので、A2 は小さくなります（n＝2 で1.880、n＝10 で0.308）。

あわせて読みたい

管理図の係数表 A2・D3・D4の一覧と使い方｜n＝2〜10の早見表と計算例

係数表を実際の管理図づくりで使う手順は、こちらで例題つきで確かめられます。

よくある質問

Step 1：管理図の「本当の目的」を理解する

まず、管理図が「本当にやりたいこと」を確認しましょう。

目的：「±3σ」の範囲に線を引きたい

管理図の管理限界線（UCL・LCL）は、「平均値 ± 3σ」の位置に引くのが基本です。なぜ3σかというと、正規分布に従うデータであれば、99.73%のデータがこの範囲に収まるからです。

つまり、管理図の本質は以下の計算です。

問題：母標準偏差σは「わからない」

ここで問題が生じます。母標準偏差σ（真のバラつき）は、通常わかりません。

全数検査でもしない限り、母集団のσを正確に知ることは不可能です。私たちが手にしているのは、サンプルデータだけです。

そこで、サンプルデータからσを「推定」する必要があります。

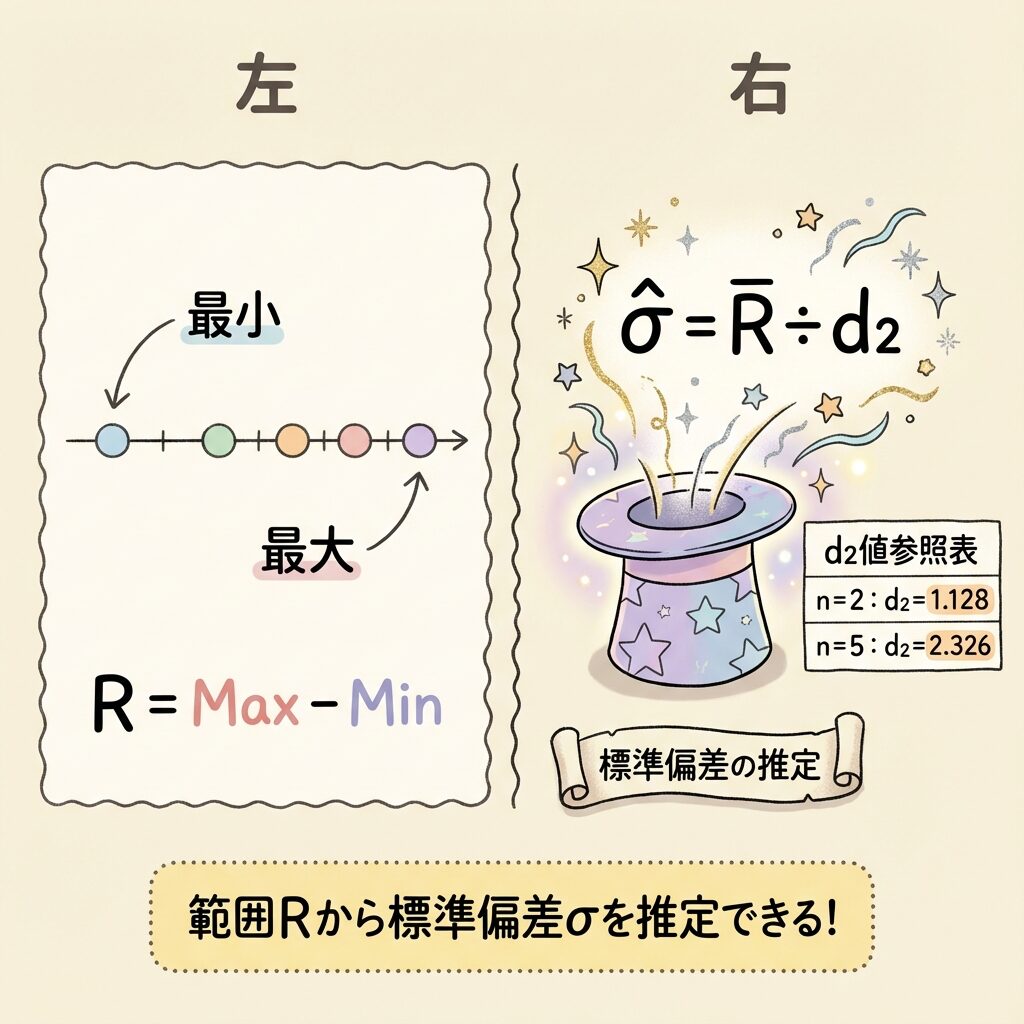
Step 2：範囲Rから標準偏差σを推定する（d2の登場）

σを推定する方法はいくつかありますが、管理図では歴史的に「範囲R」を使う方法が広く使われています。

範囲R（Range）とは？

範囲Rは、サンプル内の最大値と最小値の差です。計算がとても簡単なので、現場で使いやすいという利点があります。

例えば、5個のサンプル（10.2, 10.5, 10.1, 10.8, 10.3）があれば、R = 10.8 − 10.1 = 0.7 です。

魔法の係数「d2」：RからσへGの変換

統計学者たちは、「範囲Rと標準偏差σには一定の関係がある」ことを発見しました。

正規分布に従うデータからn個のサンプルを取ったとき、範囲Rの期待値（平均的な値）は、σのd2倍になります。

この式を変形すると、σをRから推定する式が得られます。

d2の値（サンプルサイズ別）

d2の値は、サンプルサイズnによって決まります。これも係数表に載っています。

n	2	3	4	5	6
d2	1.128	1.693	2.059	2.326	2.534

あわせて読みたい

群内変動と群間変動の違い｜X̄-R管理図での見分け方と分散の求め方

群内変動と群間変動

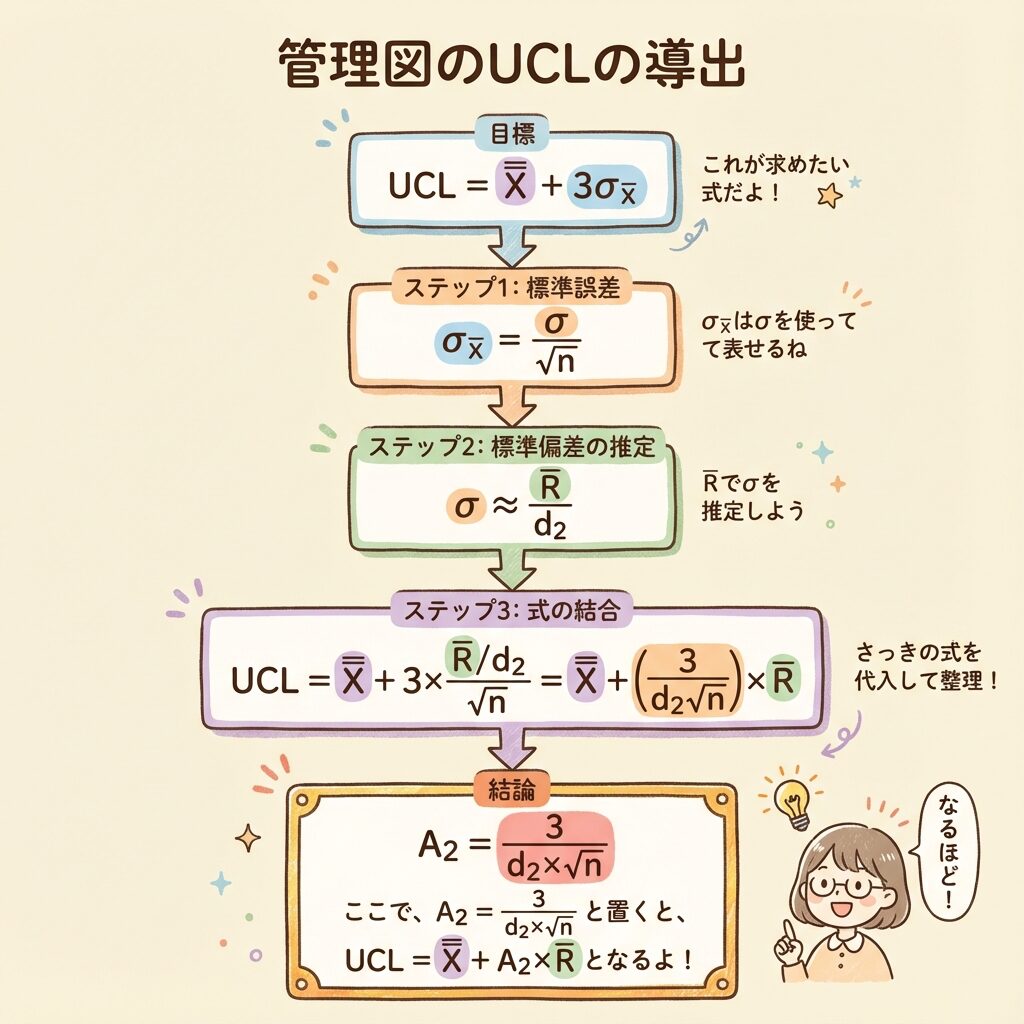
Step 3：A2の導出（X̄管理図の係数）

ここからが本題です。A2がどのように導出されるかを、ステップバイステップで見ていきましょう。

ゴール：X̄管理図のUCLを求めたい

X̄管理図では、「群ごとの平均値X̄」を打点します。この平均値のバラつきを監視したいので、管理限界線は「X̄のバラつき」に対して±3σの位置に引きます。

導出ステップ

Step 3-1：平均値の標準偏差（標準誤差）

統計学の基本定理より、n個のサンプルの平均値の標準偏差は、元のデータの標準偏差をσとすると：

Step 3-2：σをR̄/d2で置き換える

σがわからないので、σ ≈ R̄/d2 で推定します。

Step 3-3：UCLの式に代入

これをUCL = X̿ + 3σ_X̄に代入すると：

Step 3-4：A2の定義

ここで、赤字の部分をA2と定義します。

実際に計算してみる（n=5の場合）

n=5のとき、d2 = 2.326 です。これを代入すると：

係数表のA2 = 0.577と一致しました！係数は魔法の数字ではなく、ちゃんと計算で導出できるのです。

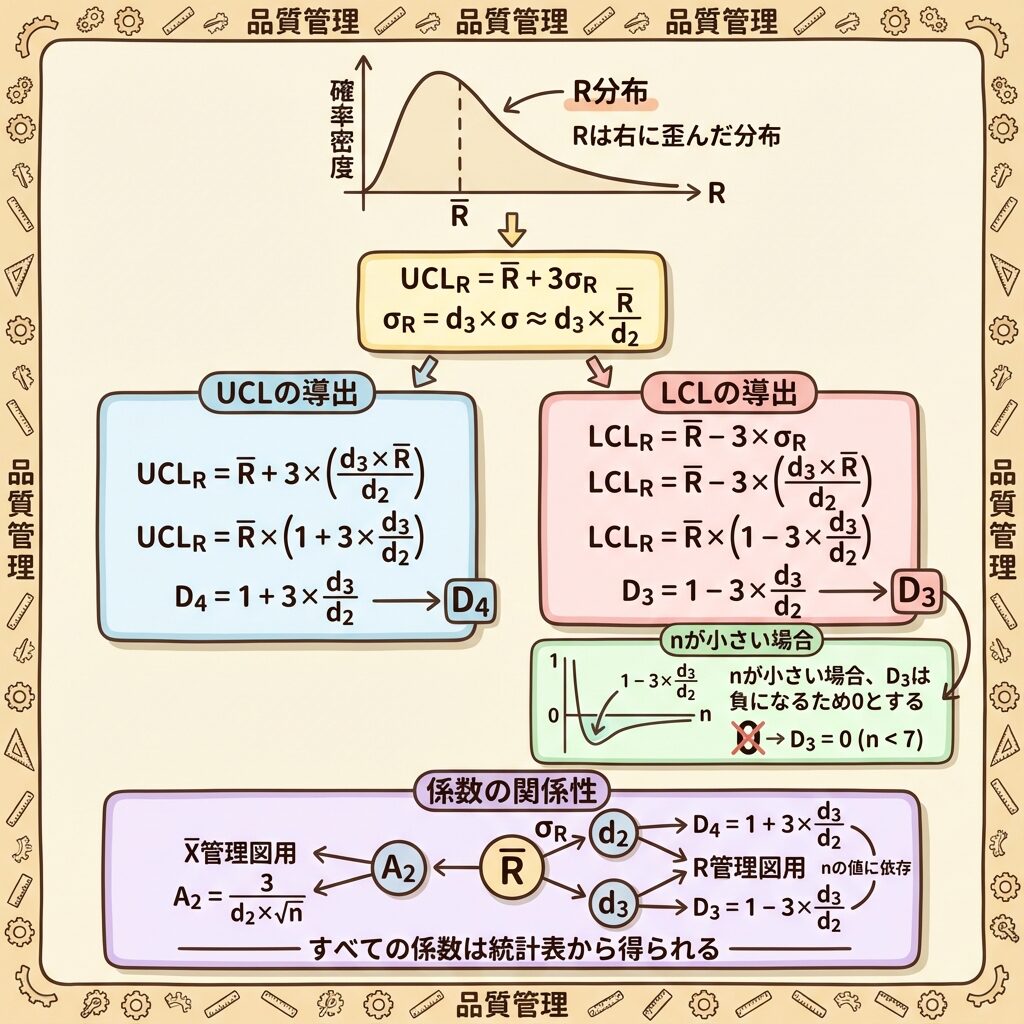
Step 4：D3・D4の導出（R管理図の係数）

R管理図の係数D3・D4も、同じ考え方で導出できます。ただし、範囲Rの分布は正規分布ではないため、少し複雑になります。

ゴール：R管理図のUCL・LCLを求めたい

導出ステップ

Step 4-1：範囲Rの標準偏差

範囲Rの標準偏差σ_Rは、元のデータの標準偏差σと係数d3を使って表せます。

d3も係数表に載っている値で、nによって決まります。

Step 4-2：σをR̄/d2で置き換える

Step 4-3：UCL・LCLの式に代入

Step 4-4：D3・D4の定義

なぜD3は「－」になることがある？

D3 = 1 − 3×(d3/d2) の計算で、3×(d3/d2) が1を超えると、D3がマイナスになります。

しかし、範囲Rは「最大値−最小値」なので、必ず0以上です。マイナスのLCLは意味がありません。

まとめ：係数の導出を図解で整理

係数は「魔法の数字」ではなく、「3σ計算をR̄で代用するための変換値」です。この原理を理解しておくと、公式の丸暗記から卒業でき、応用問題にも対応できるようになります。