修正項（CT）とは？T²/Nの計算式を図解で理解する｜一元配置実験④

📌 この記事でわかること

修正項（CT）とは何か？
なぜ「T²/N」を引くのか？
数値実験で「引く意味」を体感する
数学的な証明（なぜこの式になるのか）

こんにちは、シラスです。

実験計画法や分散分析、あるいはQC検定の勉強を始めると、必ず登場する謎の計算式があります。

📐 修正項（Correction Term）

CT = T² / N

教科書には「データの総和（T）を二乗して、データ数（N）で割れ」と書いてあります。そして、平方和（S）を求めるために、必ずこの CT を引き算させられます。

😔 こんなモヤモヤありませんか？

「計算手順は覚えたけど、これ、一体何のために引いてるの？」
「データの二乗和から引くことに、何の意味があるの？」
「そもそも『修正項』って何を『修正』してるの？」

今日は、修正項（CT）がやっている「引く作業」の正体を、具体的な数字のシミュレーションで解き明かします。

🤔 まず「修正項」という言葉について
👟 結論：修正項とは「下駄（ゲタ）」を脱がす作業
- たとえ話：身長測定と「厚底靴」
🔬 数値実験：データが「100」増えてもバラつきは同じ？
🎨 イメージ図で理解を深めよう
- イメージ①：棒グラフの「底」を持ち上げる
- イメージ②：エレベーターの「階数表示」
📐 そもそも、なぜこの式になるの？（数学的な証明）
⚠️ 実務での注意点：電卓計算のミスを防ぐ
📝 まとめ
📖 次に読む記事
🔗 関連記事
📚 一元配置実験シリーズ｜全16回

🤔 まず「修正項」という言葉について

いきなり「修正項」と言われても、何を修正するのかわかりませんよね。

実はこの名前、英語の「Correction Term」をそのまま訳したものです。

💡 なぜ「修正」と呼ぶの？

私たちが計算したいのは「データのバラつき」です。
でも、データをそのまま二乗して足すと、「平均値の分のエネルギー」も一緒に計算されてしまいます。

この「余計な分」を取り除いて、純粋なバラつきだけにする作業が「修正」です。
だから「修正項」と呼ばれます。

まだピンとこないかもしれません。でも大丈夫です。この後の数値実験で、「あ、そういうことか！」とスッキリしますよ。

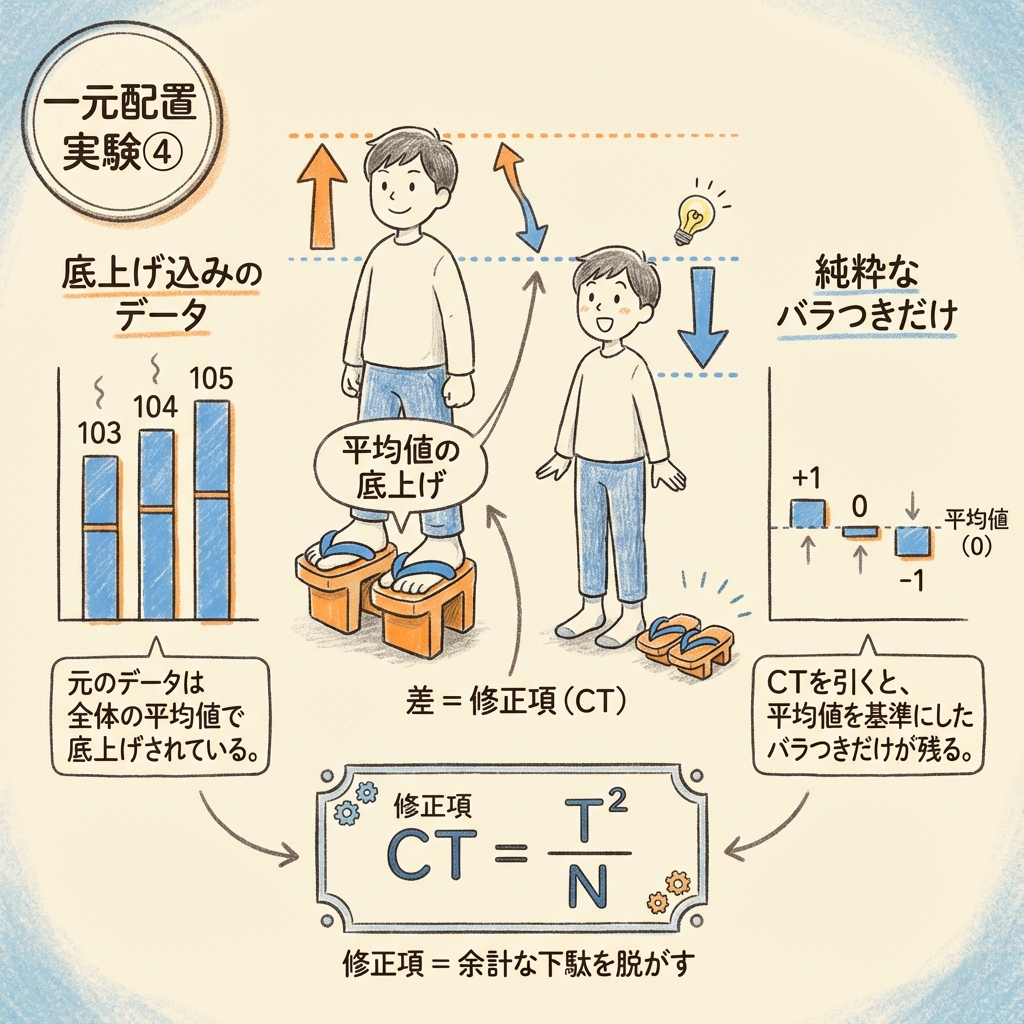
👟 結論：修正項とは「下駄（ゲタ）」を脱がす作業

まずは結論からイメージしましょう。

修正項を引くという行為は、グラフの「基準線（ゼロ点）」を平均値の位置までズラす作業です。

📊 修正項（CT）の役割

データ全体が持っている数値のうち、
「平均的な底上げ分（平均値レベル）」を取り除くこと。

🤔 なぜ引くの？

私たちが知りたいのは「平均値からのバラつき」だけ。
データの高さに含まれる「余計な標高（下駄）」が邪魔なので、CTを使ってキャンセルしている。

たとえ話：身長測定と「厚底靴」

こんな場面をイメージしてください。

3人の身長を測りたいのですが、全員が10cmの厚底靴を履いています。

Aさん：靴込みで173cm（本当は163cm）
Bさん：靴込みで174cm（本当は164cm）
Cさん：靴込みで175cm（本当は165cm）

3人の「身長のバラつき」を知りたいとき、
靴を履いたまま測っても、脱いで測っても、バラつきは同じ（±1cm）ですよね？

でも、計算するときは「靴の分（10cm）」が邪魔になります。
この「靴の分を引く」のが修正項の役割です。

まだ「ふーん」くらいかもしれません。では、実際の数字で確かめてみましょう。

🔬 数値実験：データが「100」増えてもバラつきは同じ？

ここに、2つのデータセットがあります。

📊 データA

{ 3, 4, 5 }

📊 データB

{ 103, 104, 105 }

データBは、データAに「100」を足しただけです。

直感的にわかる通り、この2つのグループの「バラつき具合」は全く同じですよね？（どちらも、真ん中から ±1 ズレているだけです）

手順1：そのまま二乗して足してみる（Σx²）

まず、何も考えずにそれぞれのデータを二乗して合計します。

データ	計算式	結果（Σx²）
データA	3² + 4² + 5² = 9 + 16 + 25	50
データB	103² + 104² + 105²	32,450

⚠️ おかしい！

バラつきは同じはずなのに、データBの方は「32,450」という巨大な数字になってしまいました。

これは、データBに含まれる「100」という「底上げ分（下駄）」も一緒に二乗して合計してしまったからです。

このままでは「バラつき」の指標として使えません。

そこで登場するのが修正項（CT）です。

手順2：修正項（T²/N）を計算する

修正項の公式を使います。

データ	合計（T）	データ数（N）	CT = T²/N
データA	12	3	12²/3 = 144/3 = 48
データB	312	3	312²/3 = 97344/3 = 32,448

データBの修正項は、ものすごく大きな値（32,448）になりました。これが「底上げ分のエネルギー」です。

手順3：引き算をする（S = Σx² − CT）

さあ、最後に引き算（修正）をします。

データ	Σx²	CT	平方和（S）
データA	50	48	2
データB	32,450	32,448	2

🎉 なんと！どちらも「2」になりました！

修正項（CT）を引くことで、データに含まれていた「100」という邪魔な下駄がきれいに消え去り、
純粋な「バラつき（2）」だけが残りました。

これが修正項の役割です。

どんなにデータが大きくても、「平均値の分のパワー」を強制的にキャンセルして、バラつきだけをあぶり出すのです。

🎨 イメージ図で理解を深めよう

数値だけではピンとこない方のために、グラフでイメージしてみましょう。

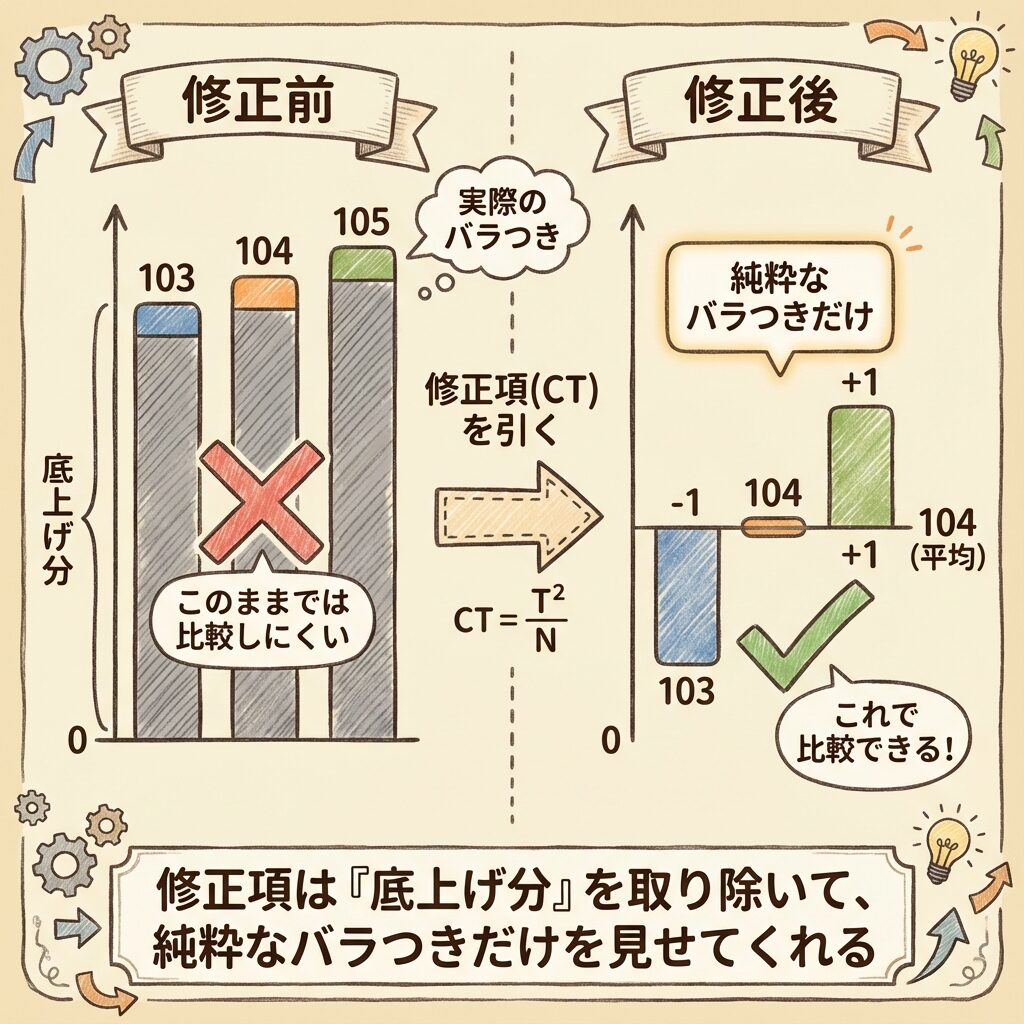
イメージ①：棒グラフの「底」を持ち上げる

【修正前】ゼロを基準にしたグラフ

データB（103, 104, 105）を棒グラフにすると、
3つの棒は「100」のあたりから伸びている。
棒の長さの大部分は「100」という共通の底上げ分。

【修正後】平均値を基準にしたグラフ

基準線を「104（平均値）」まで持ち上げると、
3つの棒は「-1, 0, +1」という純粋なズレだけを表す。
これが「修正」の意味です。

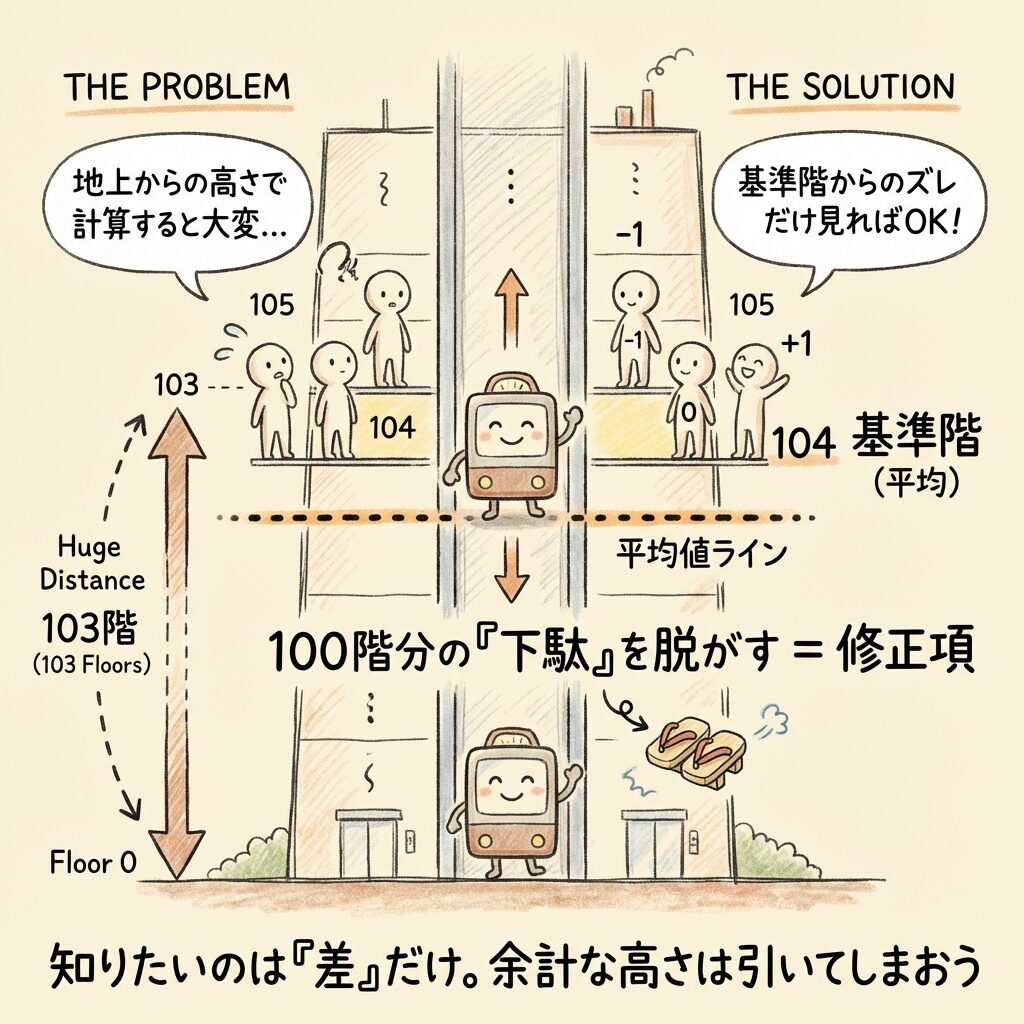
イメージ②：エレベーターの「階数表示」

100階建てのビルがあります。
3人が「103階・104階・105階」にいます。

「3人の高さの差」を知りたいとき、
わざわざ「地上からの高さ（100階分 + α）」を計算する必要はありません。

「104階を基準にして、-1階・0階・+1階」と考えればいい。

修正項は、この「100階分を引く」作業をしています。

📘 計算の全体像を確認したい方へ
一元配置実験の計算の全体像｜分散分析表を作るまでの地図｜一元配置実験③ →

📐 そもそも、なぜこの式になるの？（数学的な証明）

「意味はわかったけど、なんで T²/N を引くことになるの？」

数式が気になる方のために、中学・高校数学レベルで丁寧に証明してみましょう。

🌸 数式が苦手な方へ

この章は読み飛ばしてもOKです。
大切なのは「修正項 = 下駄を脱がす」というイメージを持つこと。
証明は「なるほど、だからこの式なのか」と納得したい人向けです。

本来、平方和（S）の定義は「偏差（平均とのズレ）の二乗の合計」です。

📐 平方和の定義
S = Σ(x − x̄)²
（各データと平均値の差を二乗して、全部足す）

このカッコの中身を展開して、Σを分配していきます。

ステップ1：カッコを展開する

(x − x̄)² = x² − 2x·x̄ + x̄²

これをΣの中に入れます。
S = Σ(x² − 2x·x̄ + x̄²)

ステップ2：Σをバラバラにする

足し算・引き算は分けて書けます。

S = Σx² − Σ(2x·x̄) + Σx̄²

ステップ3：定数を整理する（ここが重要！）

Σに関係ない「定数」を整理します。

2とx̄（平均値）は定数なので、Σの外に出せます。
最後の項のΣx̄²は、「定数x̄²をデータ数N個分足す」という意味なので、N × x̄²になります。

S = Σx² − 2x̄·Σx + N·x̄²

ステップ4：T（合計）とN（データ数）に置き換える

ここで、以下の関係式を使います。

データの合計：Σx = T
平均値：x̄ = T / N

これを式に代入して整理すると…

S = Σx² − 2(T/N)·T + N·(T/N)²
= Σx² − 2T²/N + T²/N
= Σx² − T²/N

ステップ5：完成！

S = Σx² − T²/N

後ろの部分（T²/N）が、まさに修正項（CT）です！

つまり、修正項はポッと出の公式ではなく、「偏差の二乗」を展開して整理したら自然と出てきたものなのです。

⚠️ 実務での注意点：電卓計算のミスを防ぐ

修正項の意味がわかったところで、実務（QC検定など）での計算ミスを防ぐコツをお伝えします。

🚨 一番多いミス

❌ 間違い	二乗してから、足す → Σx²
⭕️ 正解	足してから、二乗する → (Σx)² = T²

電卓を叩くときは、以下の順番を体に染み込ませてください。

🔢 電卓の手順

① まず全部足す（T）
② 「× =」で二乗する
③ データ数（N）で割る

📝 まとめ

この記事のポイント

修正項（CT）は、データの「底上げ分（平均レベル）」をキャンセルする装置
修正項を引くことで、純粋なバラつきだけが残る
数学的には、偏差の二乗を展開したら自然と出てくる式
電卓計算は「足す → 二乗 → 割る」の順番を守る

💡 こう考えると楽しくなる

修正項（CT）は、単なる計算手続きではありません。

「データを原点中心から、平均値中心の視点に切り替えるスイッチ」

こう考えると、毎回の計算が少し楽しくなりませんか？
「よし、まずはこのデータの余計な下駄（CT）を脱がせてやるか！」
と思いながら計算すれば、もう実験計画法は怖くありません。