🎯 この記事でわかること
✅ 「分散をプールする」の直感的なイメージ(お風呂のお湯で理解!)
✅ なぜプーリングすると「お得」なのか?(自由度のパワー)
✅ t検定と実験計画法での使われ方の違い
✅ 「混ぜてはいけない」危険なパターンの見分け方
目次
はじめに|「プールする」って、泳ぐプールじゃないの?
統計学を勉強していると、「プールする(Pooling)」という言葉によく出会います。
t検定では「プールした分散(Pooled Variance)」、実験計画法では「誤差項へのプーリング」…
「プール」と聞くと、どうしても水泳のプールを思い浮かべてしまいますよね。
でも、統計学での「プール」は「溜める・合算する・混ぜ合わせる」という意味です。英語の「pool」には「資源を共有する・一緒にする」という意味があるんですね。
「分散をプールする」という操作が、なぜ必要で、何をしているのかを、数式なしでイメージできるようになること。これがわかると、t検定も実験計画法も「そういうことか!」と腑に落ちます。
結論|「情報を合体させて信頼度を上げる」テクニック
まず結論から言います。
複数のグループの「バラつき(分散)」が「同じくらいだ」とみなせるとき、それらのデータをひとまとめ(プール)にして、より精度の高い「共通の分散」を計算すること。
メリットは?
データ数(自由度)が増えるため、検定の「パワー(検出力)」が上がります。つまり、微妙な差でも「有意」と判定できるようになるのです。
これだけだと抽象的なので、「お風呂のお湯」のたとえで説明しますね。
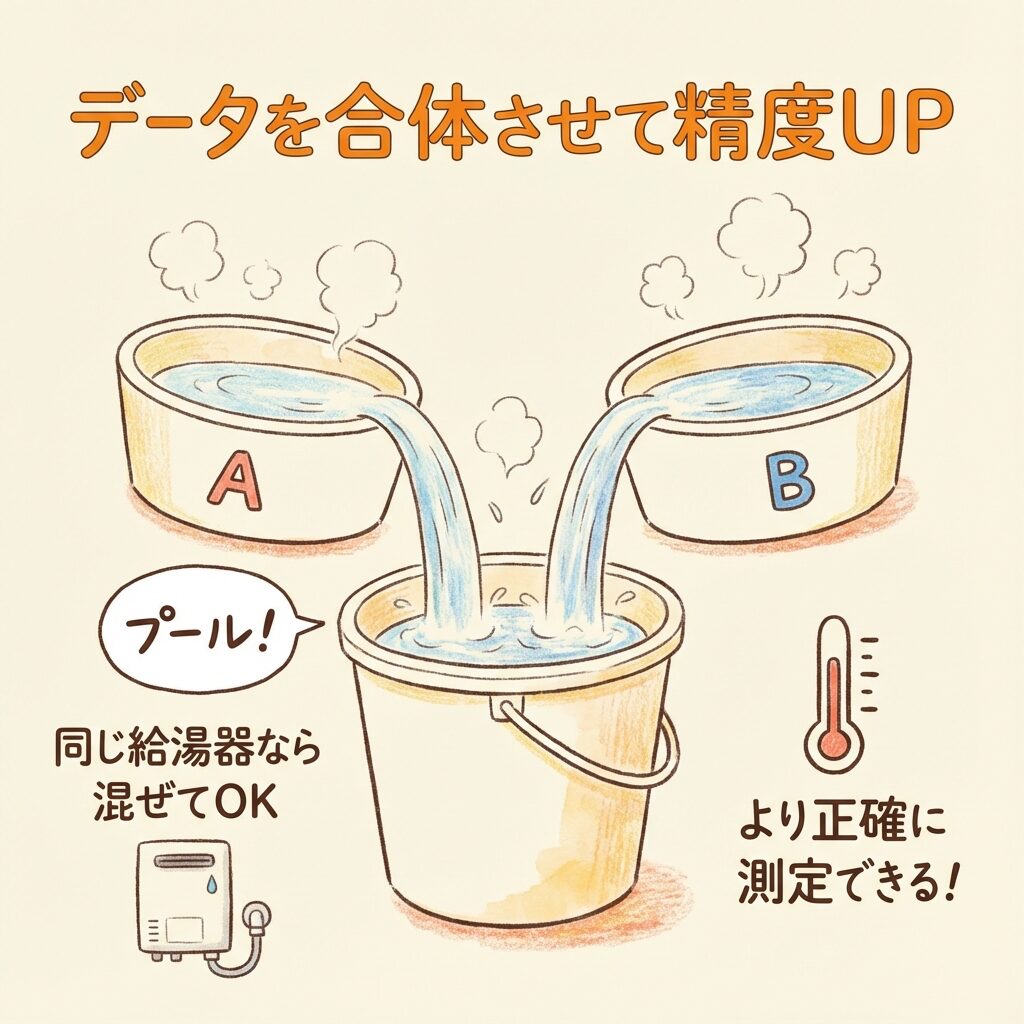
たとえ話①|お風呂のお湯で理解する「プーリング」
想像してください。あなたの家には2つの浴槽があります。
🛁 シチュエーション:2つの浴槽の温度を知りたい
浴槽A:手を入れてみた → 「だいたい40℃くらいかな?」
浴槽B:手を入れてみた → 「こっちも40℃くらいかな?」
ただし、1回ずつしか確認していないので、「本当に40℃か?」には自信がありません。
ここで問いです。
🤔 問題
「2つの浴槽は同じ給湯器から同じ設定でお湯を入れている」とわかっている場合、「お湯の温度」をより正確に知るには、どうすればいい?
💡 答え:2つの浴槽のお湯を「混ぜて」測定する
もし2つの浴槽が「同じ給湯器・同じ設定」なら、お湯の温度は本来同じはず。
だったら、2つの浴槽からお湯を汲んできて、大きなバケツで混ぜて測定したほうが、「1回ずつバラバラに測る」より正確な値が出せますよね?
これが「プーリング」の発想です。
「同じ性質を持つデータ」なら、合体させたほうがデータ数が増えて、より正確な推定ができる——これが統計学における「プール」の本質です。
🛁 お風呂のたとえ まとめ
浴槽A = グループAのデータ
浴槽B = グループBのデータ
同じ給湯器 = 「分散が同じ」という前提
バケツで混ぜる = データをプールして「共通の分散」を計算
第5回:分散と標準偏差|「バラつき」を数値化する魔法の公式 →
たとえ話②|2人の職人の「腕前」を比べる
もう少し実践的な例を見てみましょう。t検定での使われ方です。
🔧 シチュエーション:どっちの職人が速い?
ある工場で、「Aさんと Bさん、どっちが作業が速いか?」を調べるために、作業時間を5回ずつ計測しました。
| 職人 | 計測回数 | 平均作業時間 | バラつき |
|---|---|---|---|
| Aさん | 5回 | 10分 | 小さい |
| Bさん | 5回 | 12分 | 小さい |
平均を見ると、Aさんのほうが2分速い。でも、「この2分の差は偶然?それとも実力?」を判定するには、「作業時間のバラつき(標準偏差)」を基準にする必要があります。
ここで、2つの計算方法があります。
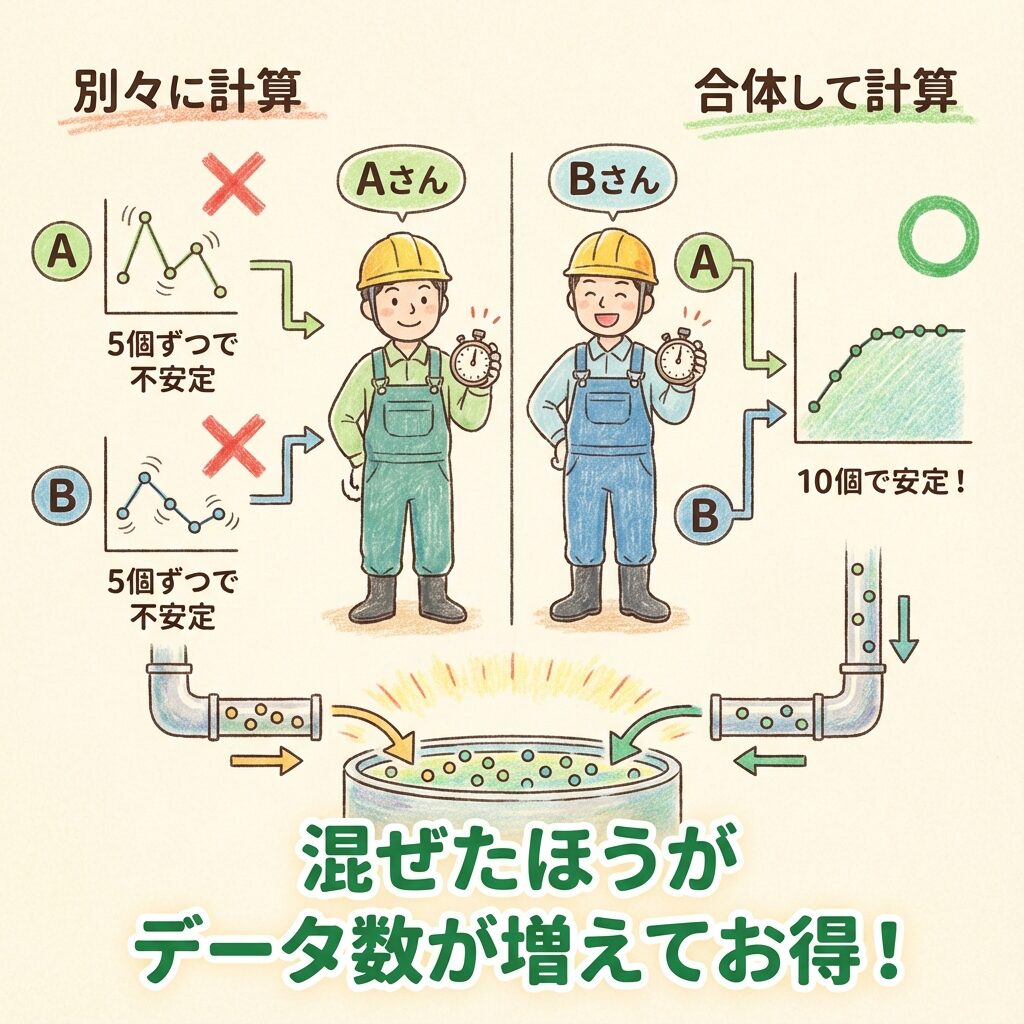
❌ 方法①:プールしない(別々に計算)
「Aさんのバラつき」はAさんの5個のデータだけで計算。
「Bさんのバラつき」はBさんの5個のデータだけで計算。
データがたった5個ずつしかないので、計算された「バラつき」の値はあまり信用できません。たまたま安定していただけかもしれない…。
これは「ウェルチのt検定」と呼ばれる手法で使われます。
⭕ 方法②:プールする(合体して計算)
ここで、もし「AさんもBさんもベテランだから、作業の安定感(分散)自体は同じくらいのはずだ」と仮定できたらどうでしょうか?
それなら、AさんとBさんのデータを「合計10個のデータ」としてひとまとめ(プール)にして、「職人の平均的な作業バラつき」を計算したほうが、より正確な値が出せますよね?
「別々に計算するより、合わせたほうがデータ数(n)が増えてお得でしょ?」という考え方。これが「スチューデントのt検定」で使われます。
なぜプーリングすると「お得」なのか?
「なぜそこまでしてデータを合体させたいの?」と思いますよね。
その理由は、統計的検定のパワーの源である「自由度」にあります。
🔍 自由度は「レンズの解像度」
統計の世界では、データ数(自由度)が増えるほど、判定用の分布(t分布)の形が鋭くなります。
これは「メガネの度数を上げる」ようなもの。解像度が上がって、「わずかな差」でも厳密に見分けられるようになるのです。
🔬 たとえ話:虫眼鏡の例
データ数が少ない = 100円ショップの虫眼鏡 → ぼんやりしか見えない
データ数が多い = 高性能顕微鏡 → 細かい差まで見える!
プーリングとは、「分散が同じ」という条件でデータを借りてきて、メガネの度数を上げる(=検定力を高める)テクニックなのです。
【完全図解】自由度とは?|「なぜn-1で割るのか」を中学生でも分かるように解説 →

実験計画法(DOE)でのプーリング
さて、この「プーリング」の考え方は、もっと複雑な「実験計画法」でも全く同じように使われます。
実験計画法では、「効果のなかった因子を誤差項(Error)にプーリングする」という操作をしますよね?
あれは一体、何をやっているのでしょうか?
🏭 たとえ話:工場の「犯人探し」
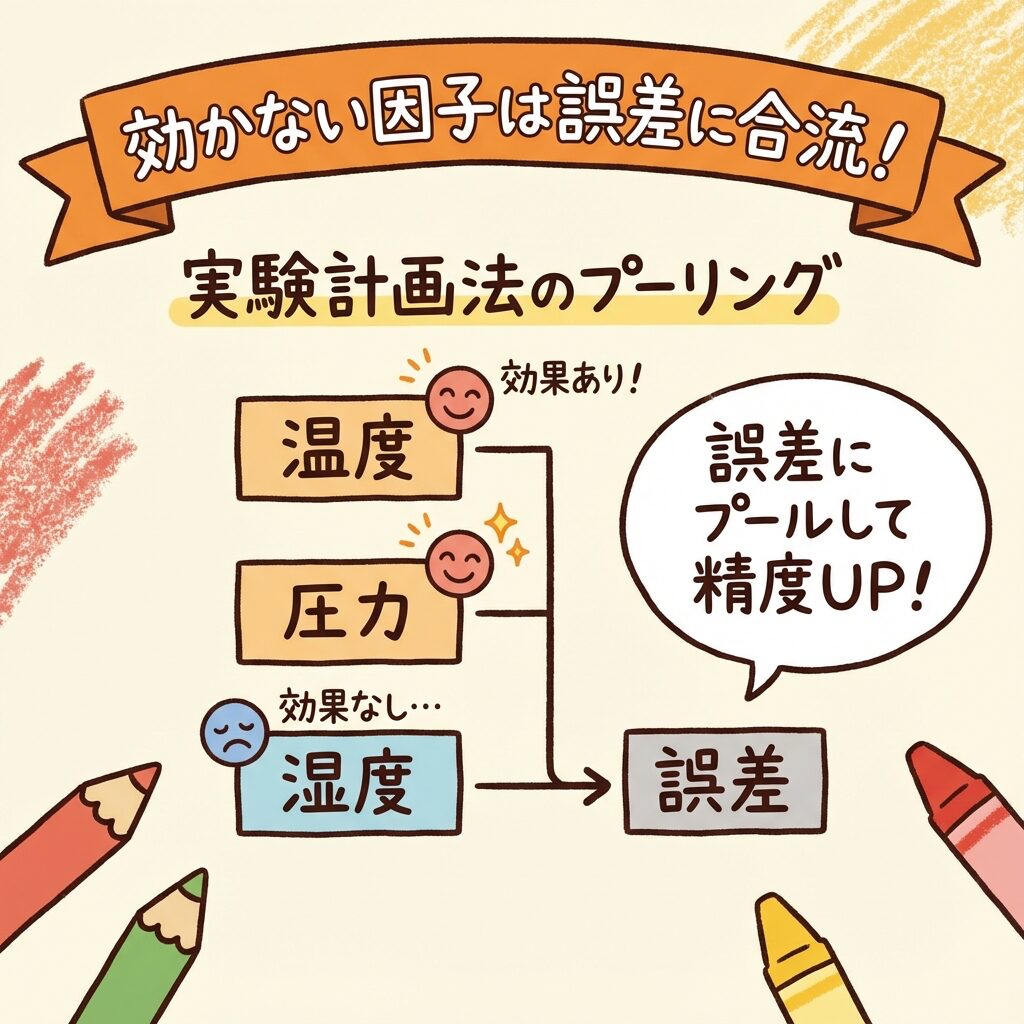
あなたは工場の品質管理担当。製品の強度がバラつく原因を突き止めたい。
容疑者は3人です。
| 容疑者(因子) | 調査結果 |
|---|---|
| 因子A:温度 | めちゃくちゃ効いてる! |
| 因子B:圧力 | まあまあ効いてる |
| 因子C:湿度 | ほぼ効いてない… |
因子C(湿度)は、調べてみたら「ほとんど強度に影響していない」ことがわかりました。
このとき、統計学ではこう考えます。
🔄 プーリングの思考プロセス
①「この因子(湿度)は、結果に影響を与えていないようだ」
②「ということは、この因子の変動は、ただの偶然のノイズ(誤差)と同じ性質のものだ」
③「だったら、誤差項と混ぜて(プールして)、誤差のデータ数を増やしてあげよう」
④「そうすれば、分母(誤差分散)の精度が上がって、本当に重要な因子(温度・圧力)をより正確に見つけられるはずだ!」
少ない実験回数(L8やL18)で戦うエンジニアにとって、「死に体の因子を誤差にプールする」ことは、「かき集められる情報は全部かき集めて、判定精度を上げる」ための生存戦略なのです。
⚠️ ただし「混ぜるな危険」のルールがある
最後に、超重要な注意点です。
プーリングは常に許されるわけではありません。
プーリングは「バラつきが同じ」という前提があって初めて成り立ちます。バラつきが明らかに違う場合、混ぜてはいけません。
🛁 お風呂のたとえで考える「混ぜるな危険」
もし2つの浴槽が「別々の給湯器」で、「温度設定も違う」としたらどうでしょう?
浴槽A:常に40℃(安定)
浴槽B:35℃〜45℃(日によってバラバラ)
この2つを混ぜて「平均的な温度」を計算しても、実態とかけ離れた値になってしまいますよね?
これと同じことが、統計でも起こります。
✅ 「混ぜていいか」を判断するルール
| 場面 | プールしていい場合 | プールしてはいけない場合 |
|---|---|---|
| t検定 | F検定で「等分散」と判定された → スチューデントのt検定 |
F検定で「不等分散」と判定された → ウェルチのt検定を使う |
| 実験計画法 | P値が大きい(効果なし)因子 → 誤差にプール |
P値が小さい(効果あり)因子 → 無理やりプールしない |
F検定(等分散の検定)「A機とB機、精度が良いのはどっち?」2つのバラつきを比較する →
まとめ|「混ぜる」は「騙す」ではなく「賢く使う」
「分散をプールする」という操作のイメージ、掴めましたか?
✅ 何をしている?
「バラつきが同じ」という条件で、データを合体させて母数(データ数)を増やしている
✅ なぜするの?
自由度が増えれば、推定の精度が上がり、検定で「差」を見つけやすくなるから
✅ 注意点は?
「バラつきが同じ」という前提が崩れたら、プールしてはいけない
統計学において「混ぜる」という行為は、決して適当にやっているわけではありません。「限られたデータの中から、少しでも真実に近づきたい」という工夫の結果なのです。
次回の実験や検定で「プール」という言葉が出てきたら、ぜひ今回のお風呂のたとえを思い出してください。きっと「あ、そういうことね」と腑に落ちるはずです。
