- 「不良率が5%→3%に減った!」でも、これって本当に改善なの?
- 母比率の検定の公式、暗記したけど「なぜこの式?」がわからない
- 二項分布から正規分布に近似できる理由を説明できない
- 計量値(平均値)の検定との違いがあいまい
- 母比率の検定が「二項分布の正規近似」であることの本質
- 検定統計量 Z = (p - P₀) / √{P₀(1-P₀)/n} が導かれる理由
- 「np > 5」の条件がなぜ必要なのか
- 不良率改善プロジェクトを例にした具体的な計算手順
こんにちは、シラスです。
前回までは「長さ」や「重さ」といった「計量値(平均値)」の検定を学んできました。今回は、製造現場やマーケティングで頻出する「比率(%)」のデータを検定する方法を解説します。
- 🏭 「不良率が 5% から 3% に減った!」
- 📺 「内閣支持率が 40% を切った!」
- 🖱 「Webサイトのクリック率が 1% 上がった!」
これらはすべて「計数値(比率)」のデータです。「たった2%の違いでしょ?誤差じゃないの?」と突っ込まれたとき、自信を持って「いいえ、統計的に有意な改善です!」と答えるための武器。それが今回紹介する「母比率の検定(大標本Z検定)」です。
この記事では、単に公式を暗記するのではなく、「なぜこの式になるのか?」を二項分布から丁寧に導出していきます。理解すれば、公式を忘れても自分で導けるようになりますよ。
目次
1. 計量値と計数値の違い|「比率」は特別なデータ
まず、検定で扱うデータには大きく2種類あることを確認しましょう。
| 種類 | 説明 | 例 | 検定方法 |
|---|---|---|---|
| 計量値 | 連続的に測れる | 長さ、重さ、温度 | t検定、Z検定(平均) |
| 計数値 | 数えられる(離散的) | 不良品数、合格者数 | Z検定(比率)、カイ二乗検定 |
計量値は「12.5cm」「68.3kg」のように小数点以下まで測れますが、計数値は「合格 or 不合格」「良品 or 不良品」のように0か1かの2択です。この「2択のデータ」を集計したものが「比率」なのです。
比率データの正体は「0と1の平均」
ここが重要なポイントです。「比率」とは何でしょうか?
たとえば、10個の製品を検査して、3個が不良品だったとします。
- 良品 → 0
- 不良品 → 1
と数値化すると、データは「0, 0, 1, 0, 0, 0, 1, 0, 0, 1」となります。この平均値は?
そう、比率 = 0と1の平均値なのです。だから「平均値の検定」と「比率の検定」は本質的に同じ構造になります。
比率 p は「0と1のデータの平均値」と同じ。だから平均値の検定と同じ発想が使える!
第3回:平均値の奥深い世界 →

2. 二項分布から正規分布へ|なぜZ検定が使えるのか?
「0か1か」の2択データは、本来二項分布という確率分布に従います。ここを理解することが、母比率の検定の本質を掴む鍵です。
二項分布とは?
二項分布は、「成功確率 P の試行を n 回繰り返したとき、成功回数 X がいくつになるか?」を表す確率分布です。
- コインを10回投げて、表が出る回数
- 200個の製品を検査して、不良品が出る個数
- 100人に調査して、賛成と答える人数
これらはすべて二項分布に従います。二項分布の特徴は、「階段状のカクカクした形」をしていることです。なぜなら、不良品の数は「0個、1個、2個...」と整数でしか取らないからです。
成功確率 P、試行回数 n のとき:
- 期待値(平均):E(X) = nP
- 分散:V(X) = nP(1-P)
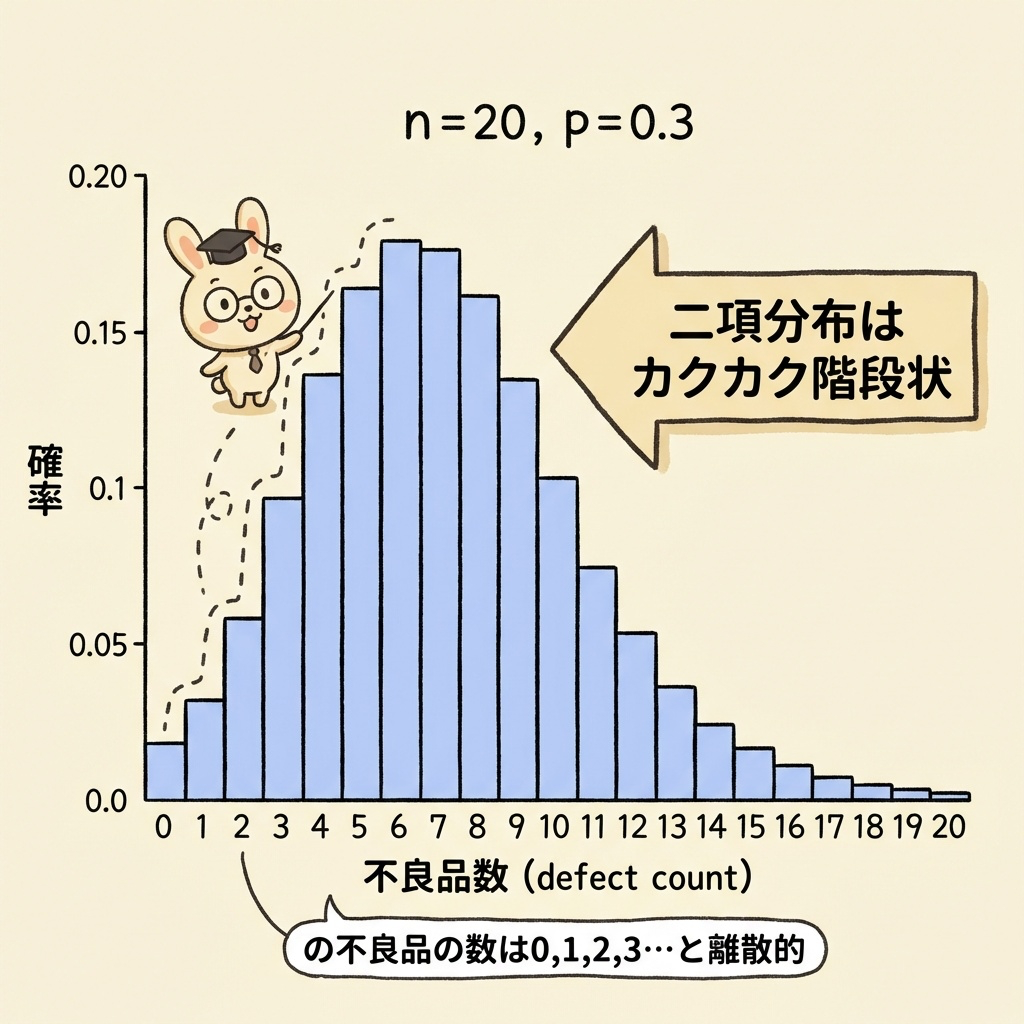
n が大きくなると「正規分布」に近づく
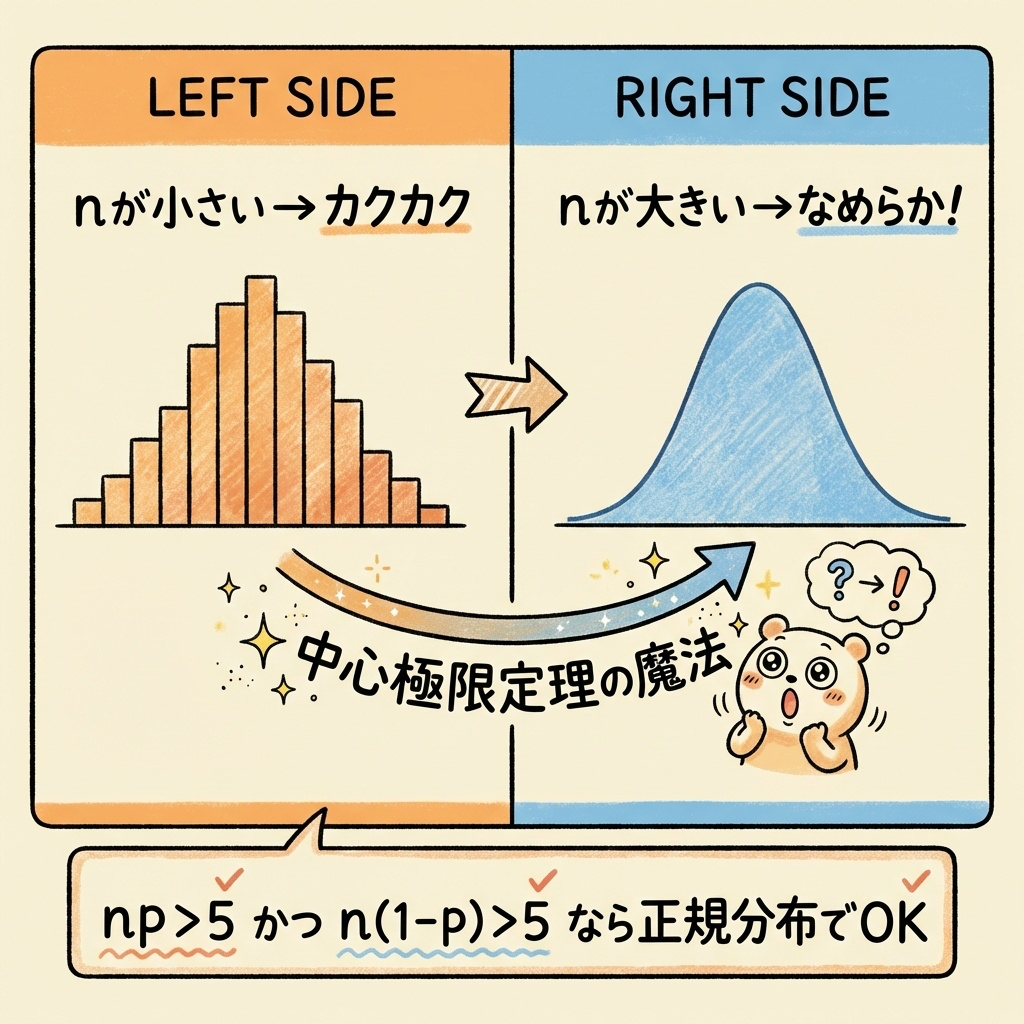
ここで「中心極限定理」の魔法が登場します。データ数 n が十分に大きいと、二項分布の階段がどんどん滑らかになり、正規分布とほぼ同じ形になるのです。
| サンプル数 n | 分布の形 | 使える検定 |
|---|---|---|
| n = 10 | カクカク階段状 | 二項検定(厳密解) |
| n = 50 | やや滑らか | 正規近似が使い始められる |
| n = 200 | ほぼ正規分布 | Z検定でOK! |
以下の両方を満たすとき、正規分布で近似できます:
nP > 5 かつ n(1-P) > 5
言い換えると「成功も失敗も、どちらも5回以上起きること」が目安です。
なぜこの条件が必要なのでしょうか?たとえば P = 0.01(1%)で n = 100 の場合、nP = 1 となり、ほとんどの場合「0個」か「1個」しか発生しません。このような偏ったデータでは、正規分布のような左右対称の釣り鐘型にはならないのです。
nP < 5 または n(1-P) < 5 のときは、正規近似を使わず「二項検定」や「フィッシャーの正確確率検定」を使いましょう。
3. 検定統計量の導出|なぜこの式になるのか?
いよいよ本題です。母比率の検定統計量 Z を、二項分布からステップバイステップで導出していきます。
Step 1:「個数 X」から「比率 p」へ変換
まず、検査で見つかった不良品の「個数」X を「比率」p に変換します。
X は二項分布 B(n, P) に従うので、p = X/n の期待値と分散は次のようになります:
比率 p の期待値
比率の期待値は、真の母比率 P そのものです。これは直感的にも納得できますね。
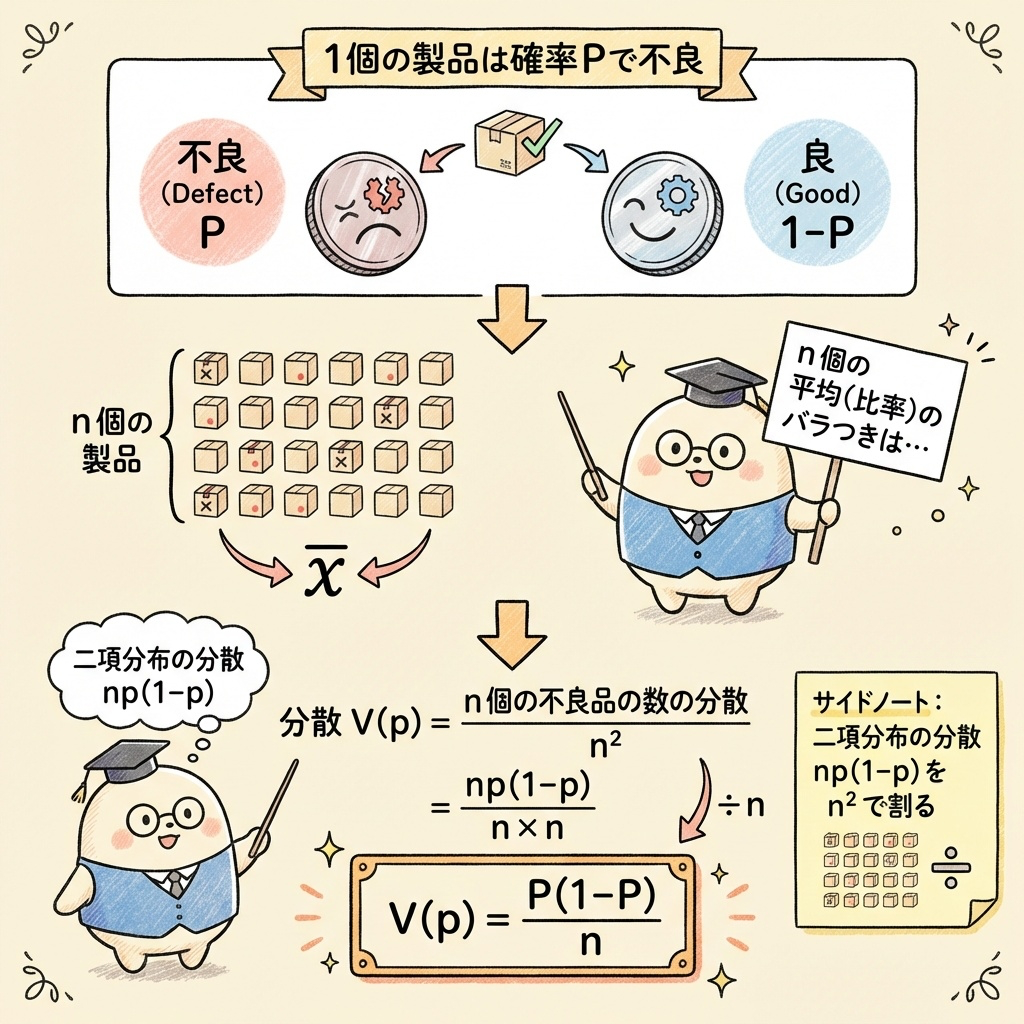
比率 p の分散
分散は少し複雑です。「定数倍したときの分散」のルールを使います。
V(aX) = a²V(X) (定数 a を掛けると、分散は a² 倍になる)
p = X/n = (1/n) × X なので、a = 1/n として:
- 期待値:E(p) = P
- 分散:V(p) = P(1-P) / n
- 標準偏差(標準誤差):√{P(1-P) / n}
Step 2:標準化してZ値を作る
正規分布に従うデータを「標準正規分布(平均0、分散1)」に変換することを標準化といいます。標準化の公式は:
比率 p を標準化すると:
- データ:p(標本比率、実測値)
- 平均:P₀(帰無仮説で想定する母比率)
- 標準偏差:√{P₀(1-P₀) / n}
p:標本比率(実測値)
P₀:帰無仮説の母比率(基準値)
n:サンプル数
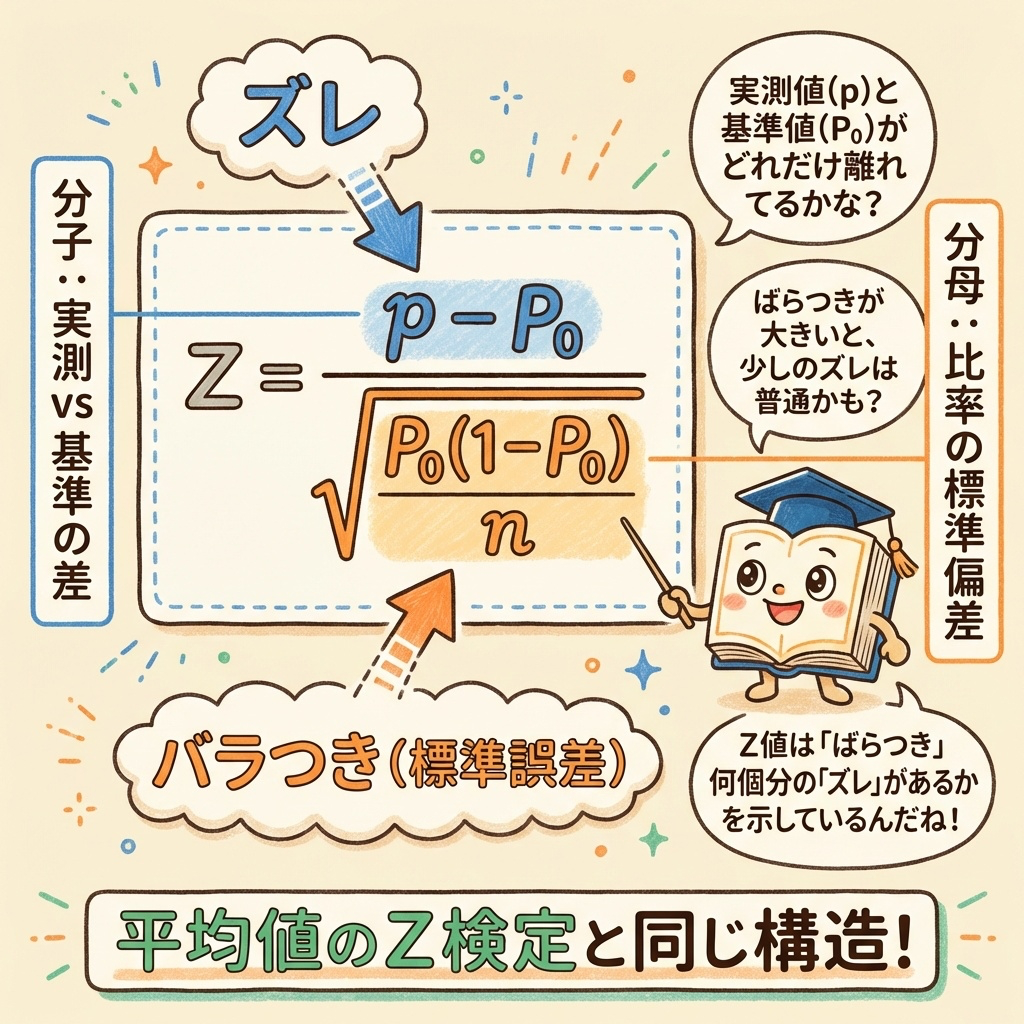
公式の意味を言葉で理解する
この公式を言葉で表すと:
| 部分 | 意味 | 例 |
|---|---|---|
| 分子(p − P₀) | 実測値と基準値の「ズレ」 | 3% − 5% = −2% |
| 分母(標準誤差) | 「偶然でどれくらいズレうるか」 | 約1.54% |
| Z値 | 「偶然のバラつき何個分ズレたか」 | 約−1.30個分 |
つまり Z値 は「観測されたズレが、偶然の範囲内かどうか」を測る物差しです。|Z| が大きければ「偶然では説明できないほどズレている」=有意差あり、と判断できます。
Z検定は「ズレ ÷ バラつき」。
ズレがバラつきの何倍かを計算して、1.96倍(両側5%)を超えたら「偶然じゃない」と判断!
4. 実践|不良率低減プロジェクトの検定
公式の意味がわかったところで、具体的な計算をしてみましょう。
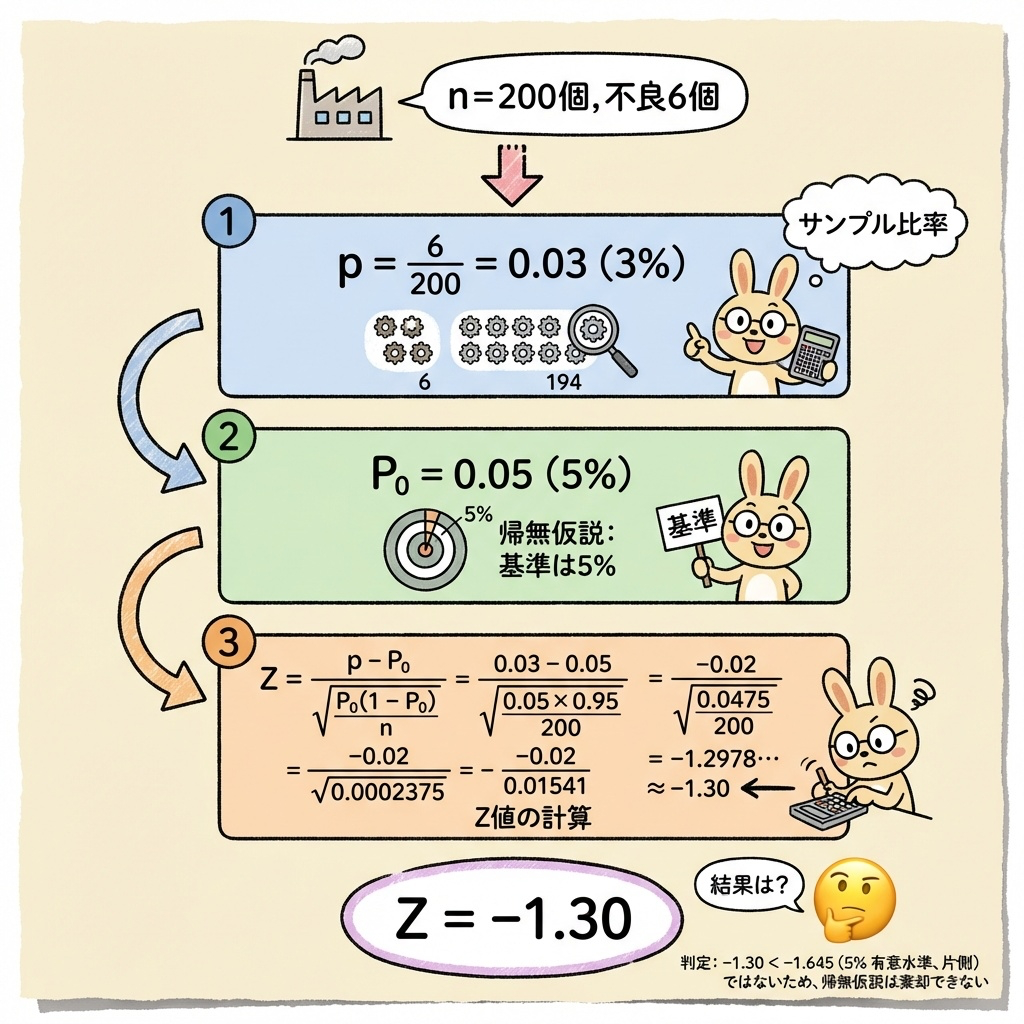
ある工場の従来の不良率は P₀ = 5%(0.05)でした。
改善活動の後、製品を n = 200個 作ったら、不良品は 6個 でした。
- 今回の不良率(標本比率):p = 6 ÷ 200 = 0.03 = 3%
「不良率が 5% → 3% に減ったのは、改善効果か? それとも偶然か?」
有意水準 5%、片側検定(「減ったこと」を確認したい)で検定せよ。
Step 1:仮説を立てる
- 帰無仮説 H₀:P = 0.05(不良率は5%のまま、改善されていない)
- 対立仮説 H₁:P < 0.05(不良率は5%より低くなった=改善された)
「減ったかどうか」を検証したいので、片側検定(左側)を使います。
Step 2:正規近似の条件を確認
Z検定を使うには、正規近似の条件 nP > 5 かつ n(1-P) > 5 を満たす必要があります。
- nP₀ = 200 × 0.05 = 10 → 5以上 ✅
- n(1-P₀) = 200 × 0.95 = 190 → 5以上 ✅
両方とも5を超えているので、正規近似OKです。Z検定が使えます!
Step 3:Z値を計算する
公式に数値を代入します。
まず分母(標準誤差)を計算
次にZ値を計算
Z ≈ −1.30
Step 4:判定する(臨界値との比較)
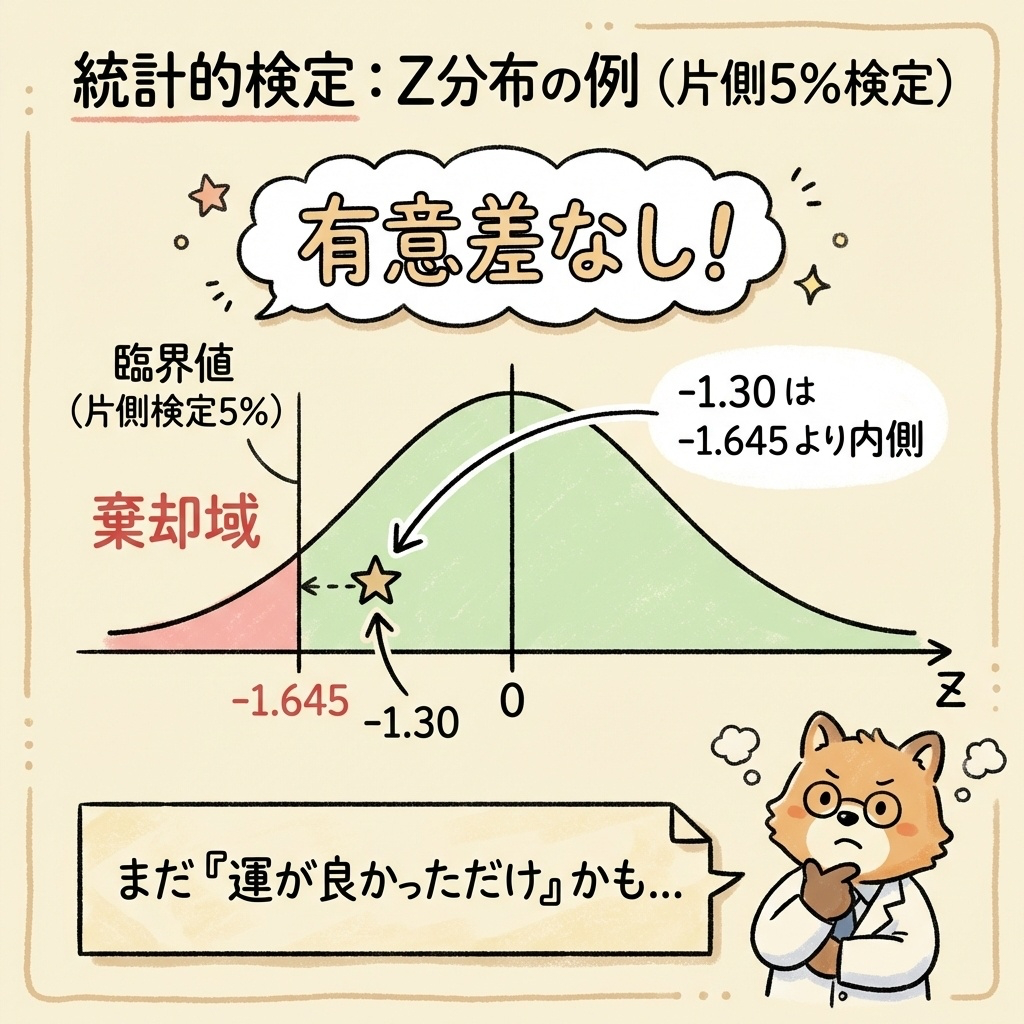
今回は片側検定(左側)なので、有意水準5%の臨界値は −1.645 です。
| 検定の種類 | 有意水準 5% | 有意水準 1% |
|---|---|---|
| 両側検定 | ±1.96 | ±2.58 |
| 片側検定 | ±1.645 | ±2.33 |
計算した Z = −1.30 を臨界値 −1.645 と比較します。
- 計算値:Z = −1.30
- 臨界値:−1.645
Z = −1.30 は臨界値 −1.645 より右側(0に近い側)にあります。つまり、棄却域に入っていません。
|Z| = 1.30 < 1.645
帰無仮説を棄却できない(有意差なし)
Step 5:結論を述べる
「200個作って不良率が5%→3%に減った!やったー!」と喜んでいましたが、
統計学的には「いや、運が良かっただけでしょ(実力は5%のままかもよ)」と判定されてしまいました。
これが統計学の厳しい(でも公正な)ジャッジです。2%の差は、200個程度のサンプルでは「偶然の範囲内」として片付けられてしまうのです。
もし「有意」にしたいなら?
同じ3%の不良率でも、サンプル数を増やせば有意差が出る可能性があります。たとえば n = 500 なら:
- 標準誤差 = √{0.05 × 0.95 / 500} ≈ 0.00975
- Z = (0.03 − 0.05) / 0.00975 ≈ −2.05
|Z| = 2.05 > 1.645 なので、n = 500 なら有意差ありと判定できます!
比率の検定では「小さな差を検出するには、大きなサンプル数が必要」。実験計画の段階でサンプル数を決めることが重要です。
統計学のおすすめ書籍
統計学の「数式アレルギー」を治してくれた一冊
「Σ(シグマ)や ∫(インテグラル)を見ただけで眠くなる…」 そんな私を救ってくれたのが、小島寛之先生の『完全独習 統計学入門』です。
この本は、難しい記号を一切使いません。 「中学レベルの数学」と「日本語」だけで、検定や推定の本質を驚くほど分かりやすく解説してくれます。
「計算はソフトに任せるけど、統計の『こころ(意味)』だけはちゃんと理解したい」 そう願う学生やエンジニアにとって、これ以上の入門書はありません。
【QC2級】「どこが出るか」がひと目で分かる!最短合格へのバイブル
私がQC検定2級に合格した際、使い倒したのがこの一冊です。
この本の最大の特徴は、「各単元の平均配点(何点分出るか)」が明記されていること。 「ここは出るから集中」「ここは出ないから流す」という戦略が立てやすく、最短ルートで合格ラインを突破できます。
解説が分かりやすいため、私はさらに上の「QC1級」を受験する際にも、基礎の確認用として辞書代わりに使っていました。 迷ったらまずはこれを選んでおけば間違いありません。


