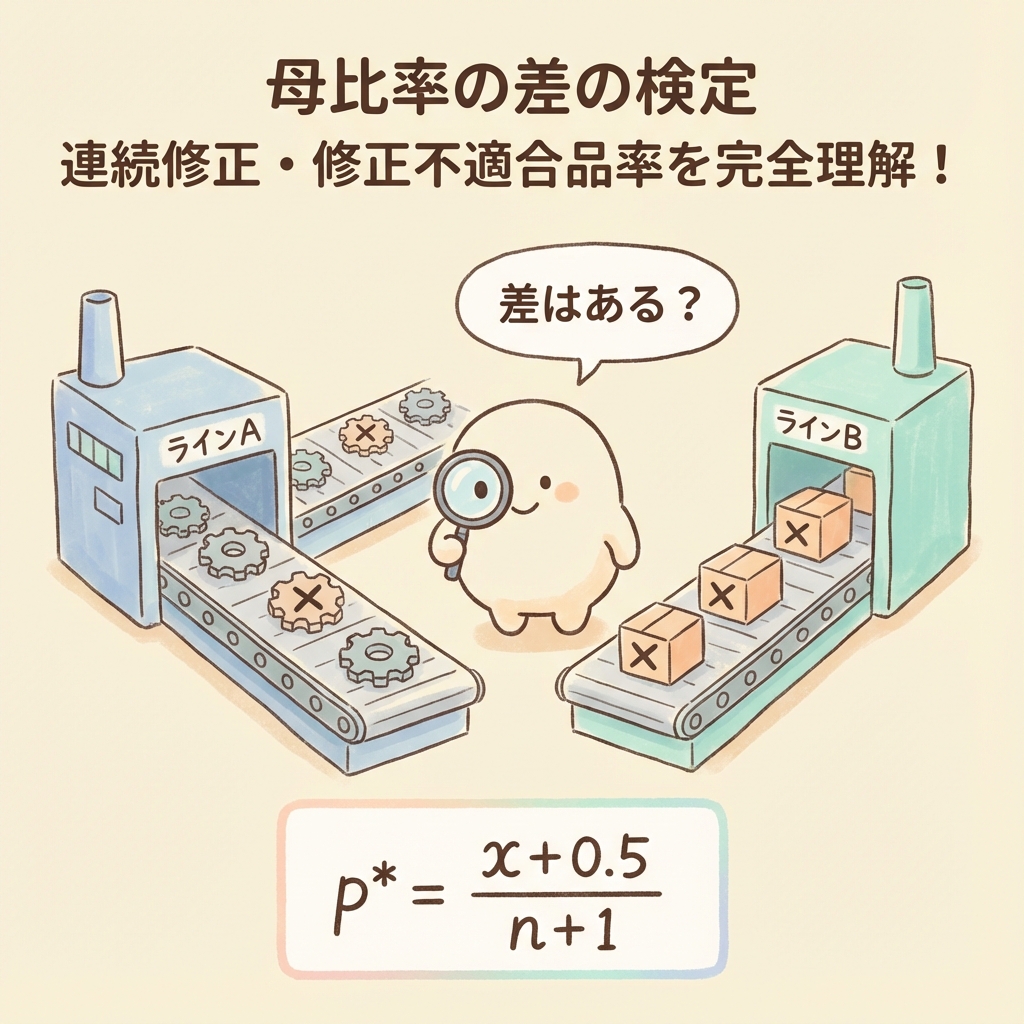
- 「修正不適合品率」の式 p* = (x+0.5)/(n+1) が突然出てきて意味不明…
- なぜ分子に+0.5、分母に+1を足すの?
- 「連続修正」「プール推定」の関係がごちゃごちゃ…
- QC検定1級の計数値の検定問題が解けない
- なぜ「連続修正」が必要なのか、階段と坂道の比喩で直感理解
- 修正不適合品率 p* = (x+0.5)/(n+1) の式の「なぜ」
- プール推定(併合推定)の意味と計算方法
- 実際の問題をStep by Stepで完全攻略
QC検定1級の計数値データの検定で、こんな式を見たことはありませんか?
p* = (x + 0.5) / (n + 1)
普通の不適合品率は p = x/n なのに、なぜ分子に+0.5、分母に+1を足すのか?
この記事では、この「なぜ」を徹底的に解説します。式を暗記するのではなく、「こういう理由だからこの式になる」と納得できるようになりましょう。
目次
この記事で扱う問題の全体像
まず、どんな問題を解くのかを把握しましょう。
📋 典型的な問題設定
【問題】
ある会社では、部品QをラインAとラインBの2つの製造ラインで生産している。各ラインからランダムに製品を抽出して外観検査を行い、以下のデータを得た。
| 工程 | 検査個数 n | 不適合品数 x |
|---|---|---|
| ラインA | 500 | 32 |
| ラインB | 700 | 49 |
2つのラインの母不適合品率に差があるか、有意水準5%で検定せよ。
🗺️ 解答までのロードマップ
この問題を解くには、以下の知識が必要です。
| ステップ | 必要な知識 | この記事での解説 |
|---|---|---|
| ① | なぜ「修正」が必要か | ブロック② |
| ② | 修正不適合品率 p* の計算 | ブロック③ |
| ③ | プール推定(併合推定) | ブロック④ |
| ④ | 検定統計量 u₀ の計算 | ブロック⑤ |
| ⑤ | 判定と結論 | ブロック⑥ |
それでは、順番に見ていきましょう!
Step1:なぜ「連続修正」が必要なのか?
まず、最も根本的な疑問から解決しましょう。なぜ「修正」が必要なのか?
🎯 計数値データの本質:「飛び飛び」の値
不適合品数 x は、0, 1, 2, 3, ... という整数値しか取りません。
「2.5個の不良品」なんてありえませんよね?これを離散データといいます。
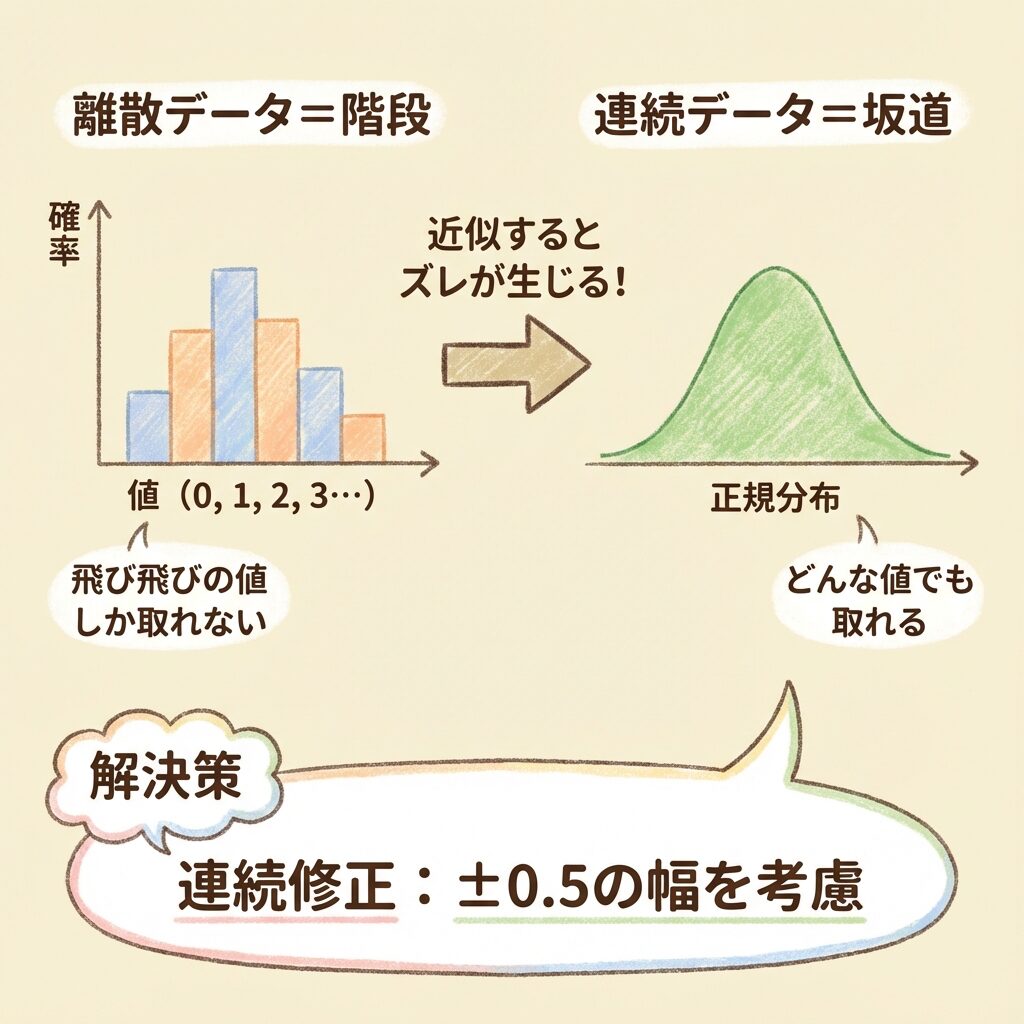
離散データは「階段」のようなもの。1段、2段、3段…と、飛び飛びの値しか取れません。
📊 正規分布の本質:「なめらか」な曲線
一方、検定で使う正規分布は、どんな値でも取れる連続分布です。
2.5も、2.73も、2.999も、すべて取りうる値です。
連続分布は「なめらかな坂道」のようなもの。どの位置にも立てます。
⚠️ 問題:「階段」を「坂道」で近似する矛盾
計数値データの検定では、離散的な二項分布を連続的な正規分布で近似します。
これは便利ですが、問題があります。
「階段」を「坂道」で近似すると、確率の計算にズレが生じます。特にサンプルサイズが小さいとき、このズレが無視できません。
🔧 解決策:連続修正(Yatesの修正)
この「ズレ」を補正するのが連続修正(Yatesの連続修正)です。
具体的には、離散値を±0.5の幅を持つ区間として扱います。
離散値「3」は、連続値では「2.5〜3.5」の区間に対応する
例:不適合品数 x = 3 のとき
→ 連続値では 2.5 ≤ X < 3.5 の区間として扱う
🎨 視覚的に理解する:階段と坂道の対応
下の図をイメージしてください。
| 離散値(階段) | 連続値(坂道)での対応区間 |
|---|---|
| x = 0 | -0.5 ≤ X < 0.5 |
| x = 1 | 0.5 ≤ X < 1.5 |
| x = 2 | 1.5 ≤ X < 2.5 |
| x = 3 | 2.5 ≤ X < 3.5 |
こうすることで、「階段」の各段が「坂道」の一定区間に対応し、確率計算の精度が上がります。
連続修正とは、離散データを連続分布で近似するときの「ズレ」を補正するため、±0.5の幅を考慮する手法です。
Step2:修正不適合品率 p* の意味と導出
連続修正の考え方がわかったところで、本題の修正不適合品率の式を見ていきましょう。
📊 通常の不適合品率と修正不適合品率の比較
| 種類 | 式 | 使う場面 |
|---|---|---|
| 通常の不適合品率 | p = x / n | 単純な比率の計算 |
| 修正不適合品率 | p* = (x + 0.5) / (n + 1) | 正規近似の精度向上 |
なぜ、分子に+0.5、分母に+1を足すのでしょうか?
🔍 理由①:分子の+0.5は「連続修正」
先ほど学んだ連続修正の考え方を思い出してください。
離散値 x は、連続値では「x - 0.5 から x + 0.5 の区間」に対応します。
この区間の中央値を使うと、ちょうど x になります。しかし、正規分布の対称性を考慮すると、少し調整が必要です。
不適合品数 x を「x + 0.5」に修正することで、連続分布への近似精度を高めています。
直感的には:「xちょうど」ではなく「xの上限側(x + 0.5)」を使うことで、確率計算のズレを補正
🔍 理由②:分母の+1は「ベイズ的調整」
分母の+1は、少し違う理由から来ています。これはベイズ統計の考え方に基づいています。
極端な値を避ける問題
通常の不適合品率 p = x/n には、問題があります。
- x = 0 のとき、p = 0(不良率ゼロ)
- x = n のとき、p = 1(不良率100%)
しかし、「たまたま今回のサンプルで不良が出なかった」からといって、本当の不良率がゼロとは限りませんよね?
サンプルサイズが小さいとき、p = 0 や p = 1 という極端な推定値が出やすく、検定の精度が落ちます。
解決策:分子に+0.5、分母に+1を足す
修正不適合品率 p* = (x + 0.5) / (n + 1) を使うと:
- x = 0 のとき、p* = 0.5 / (n + 1) ≠ 0
- x = n のとき、p* = (n + 0.5) / (n + 1) ≠ 1
つまり、極端な値(0や1)を避けることができます。
ベイズ統計では「事前に何も情報がない状態」を表すのに、一様分布 Beta(1, 1) を使います。
この事前分布を考慮すると、推定値は:
p* = (x + 0.5) / (n + 1)
となります。これは「Jeffreysの事前分布」に基づく推定値に近い形です。
🧮 実際に計算してみよう
先ほどの問題のデータで、修正不適合品率を計算してみます。
| 工程 | n | x | 通常 p = x/n | 修正 p* = (x+0.5)/(n+1) |
|---|---|---|---|---|
| ラインA | 500 | 32 | 0.0640 | 0.0649 |
| ラインB | 700 | 49 | 0.0700 | 0.0706 |
ラインAの計算
p*A = (xA + 0.5) / (nA + 1) = (32 + 0.5) / (500 + 1) = 32.5 / 501 = 0.0649
ラインBの計算
p*B = (xB + 0.5) / (nB + 1) = (49 + 0.5) / (700 + 1) = 49.5 / 701 = 0.0706
修正不適合品率は、通常の不適合品率よりわずかに大きな値になります。これは「極端な値を避ける」ための調整が効いているからです。

Step3:プール推定(併合推定)の意味と計算
次に、プール推定(併合推定)について学びましょう。これは検定統計量を計算する上で必須の知識です。
🤔 なぜプール推定が必要なのか?
母比率の差の検定では、以下の仮説を検定します。
帰無仮説 H₀:PA = PB(= P)… 2つのラインの母不適合品率は等しい
対立仮説 H₁:PA ≠ PB … 2つのラインの母不適合品率は異なる
ここで重要なのは、帰無仮説H₀が正しいと仮定したとき、2つのラインの母不適合品率は同じ値Pだということです。
「2つのラインは同じ母不適合品率Pを持つ」と仮定するなら、2つのデータを合わせて1つの推定値を求めた方が精度が良いですよね。これがプール推定です。
🥤 イメージ:2つのジュースを1つの容器に混ぜる
ラインAとラインBのデータを「プール」(pool = 合わせる、貯める)するイメージです。
- ラインA:500個中32個が不適合
- ラインB:700個中49個が不適合
- 合計:1200個中81個が不適合
2つのグラスのジュースを1つの大きな容器に混ぜるように、2つのデータを1つにまとめます。
📐 プール推定値の計算式
通常版(修正なし)
p̂ = (xA + xB) / (nA + nB)
修正版(連続修正あり)
p* = (xA + xB + 0.5) / (nA + nB + 1)
修正版では、先ほど学んだ修正不適合品率と同じ考え方で、分子に+0.5、分母に+1を足します。
🧮 実際に計算してみよう
問題のデータでプール推定値を計算します。
| 項目 | ラインA | ラインB | 合計 |
|---|---|---|---|
| 検査個数 n | 500 | 700 | 1200 |
| 不適合品数 x | 32 | 49 | 81 |
修正プール推定値の計算
p* = (xA + xB + 0.5) / (nA + nB + 1)
p* = (32 + 49 + 0.5) / (500 + 700 + 1)
p* = 81.5 / 1201
p* = 0.0679
p* = 0.0679
これは「2つのラインが同じ」と仮定したときの、共通の母不適合品率の推定値です。
検定統計量の分母(標準誤差)を計算するとき、帰無仮説が正しいと仮定した状態での母比率が必要です。プール推定値は、この「帰無仮説の下での母比率」を推定した値なのです。

Step4:検定統計量 u₀ の公式と導出
いよいよ、検定統計量の計算に入ります。ここまでの知識を総動員しましょう。
📐 検定統計量の一般形
母比率の差の検定統計量は、以下の形をしています。
u₀ = (推定値の差) / (標準誤差)
これは、すべての検定統計量に共通する構造です。「差がどれだけ標準誤差の何倍分あるか」を表しています。
🔢 分子:修正不適合品率の差
分子は、2つのラインの修正不適合品率の差です。
分子 = p*A − p*B
先ほど計算した値を使うと:
分子 = 0.0649 − 0.0706 = −0.0057
🔢 分母:標準誤差の導出
分母の標準誤差が、この検定の核心部分です。なぜこの式になるのか、丁寧に導出しましょう。
Step 4-1:各ラインの標本比率の分散
母比率がPのとき、サンプルサイズnの標本比率p̂の分散は:
これは二項分布から導かれる公式です。
Step 4-2:差の分散
2つの独立な確率変数の差の分散は、分散の和になります(分散の加法性)。
= PA(1−PA)/nA + PB(1−PB)/nB
Step 4-3:帰無仮説の下での簡略化
帰無仮説H₀:PA = PB = P の下では、上の式は簡略化できます。
= P(1−P) × (1/nA + 1/nB)
Step 4-4:標準誤差(分散の平方根)
標準誤差は分散の平方根なので:
SE = √[ P(1−P) × (1/nA + 1/nB) ]
Step 4-5:Pの代わりにプール推定値p*を使う
母比率Pは未知なので、先ほど計算したプール推定値p*で代用します。
SE = √[ p*(1−p*) × (1/nA + 1/nB) ]
📐 検定統計量の完成形
以上をまとめると、検定統計量u₀は次のようになります。
u₀ = (p*A − p*B) / √[ p*(1−p*) × (1/nA + 1/nB) ]
p*A, p*B:各ラインの修正不適合品率
p*:プール推定値(修正あり)
nA, nB:各ラインのサンプルサイズ
🧮 実際に計算してみよう
これまでに計算した値をまとめます。
| 記号 | 意味 | 値 |
|---|---|---|
| nA | ラインAのサンプルサイズ | 500 |
| nB | ラインBのサンプルサイズ | 700 |
| p*A | ラインAの修正不適合品率 | 0.0649 |
| p*B | ラインBの修正不適合品率 | 0.0706 |
| p* | プール推定値(修正あり) | 0.0679 |
計算① 分子を計算
分子 = p*A − p*B = 0.0649 − 0.0706 = −0.0057
計算② p*(1−p*)を計算
p*(1−p*) = 0.0679 × (1 − 0.0679) = 0.0679 × 0.9321 = 0.0633
計算③ (1/nA + 1/nB)を計算
1/nA + 1/nB = 1/500 + 1/700 = 0.00200 + 0.00143 = 0.00343
計算④ 分母(標準誤差)を計算
SE = √[ 0.0633 × 0.00343 ] = √0.000217 = 0.0147
計算⑤ 検定統計量u₀を計算
u₀ = 分子 / 分母 = −0.0057 / 0.0147 = −0.388
u₀ = −0.388
Step5:判定と結論
検定統計量u₀ = −0.388 が得られました。これを有意水準5%で判定します。
📊 判定基準(両側検定)
対立仮説が H₁:PA ≠ PB(両側対立)なので、両側検定を行います。
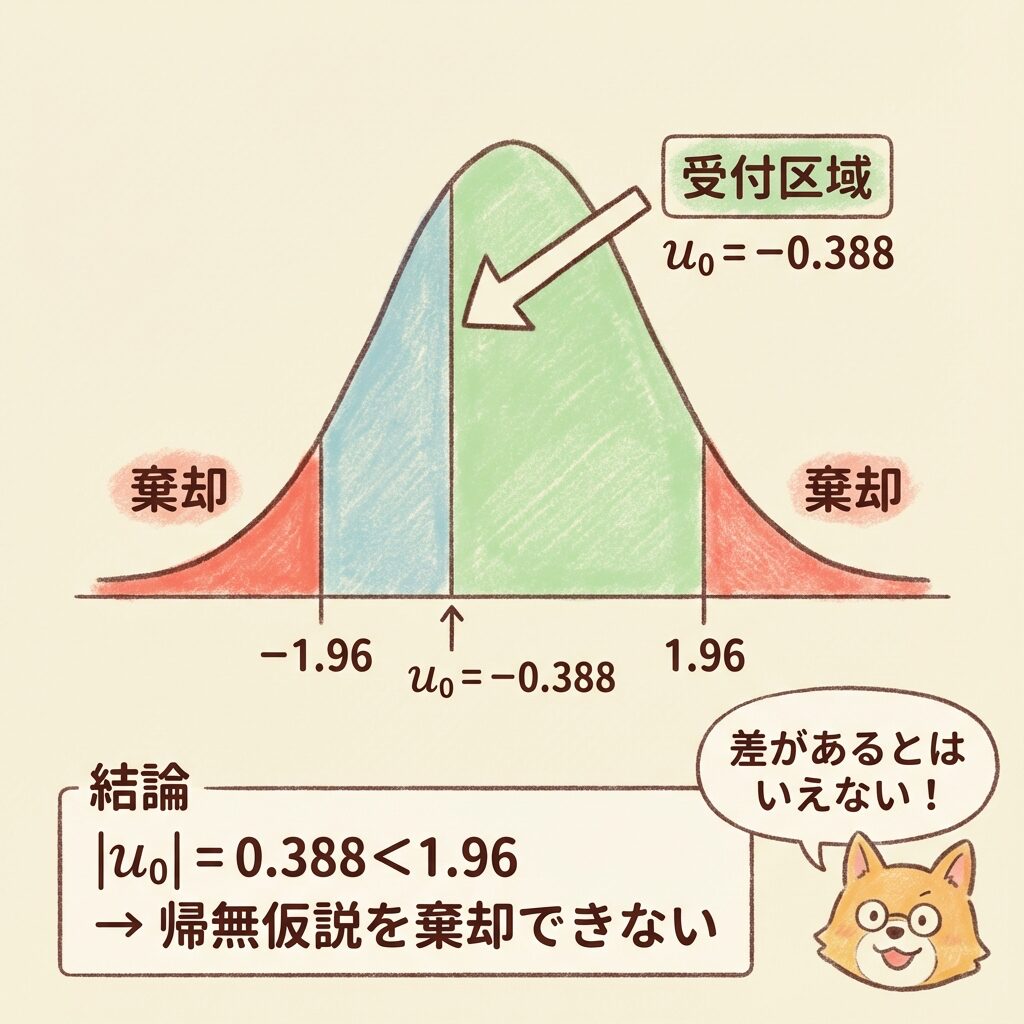
両側検定の棄却域:|u₀| > zα/2 = z0.025 = 1.96
つまり、u₀ < −1.96 または u₀ > 1.96 のとき、帰無仮説を棄却
⚖️ 判定
検定統計量と棄却域を比較します。
| 項目 | 値 |
|---|---|
| 検定統計量 |u₀| | |−0.388| = 0.388 |
| 棄却限界値 | 1.96 |
| 比較 | 0.388 < 1.96 |
|u₀| = 0.388 < 1.96 なので、帰無仮説を棄却できません。
📝 結論
有意水準5%で検定すると、ラインAとラインBにおいては、母不適合品率に差があるとはいえない。
「差がない」と断定しているわけではありません。「今回のデータからは、差があるとは言い切れなかった」という意味です。
ラインAの不良率(約6.5%)とラインBの不良率(約7.1%)の差は、サンプリングによる偶然の変動の範囲内と考えられます。
全体のまとめ:計算フローチャート
母比率の差の検定(連続修正あり)の全体の流れをまとめます。
📋 計算の全体フロー
【Step 1】各ラインの修正不適合品率を計算
p*A = (xA + 0.5) / (nA + 1)
p*B = (xB + 0.5) / (nB + 1)
【Step 2】プール推定値(修正あり)を計算
p* = (xA + xB + 0.5) / (nA + nB + 1)
【Step 3】検定統計量を計算
u₀ = (p*A − p*B) / √[ p*(1−p*)(1/nA + 1/nB) ]
【Step 4】判定
両側検定(α = 0.05):|u₀| > 1.96 なら帰無仮説を棄却
📊 今回の問題の計算結果まとめ
| ステップ | 計算内容 | 結果 |
|---|---|---|
| Step 1-A | p*A = (32+0.5)/(500+1) | 0.0649 |
| Step 1-B | p*B = (49+0.5)/(700+1) | 0.0706 |
| Step 2 | p* = (81+0.5)/(1200+1) | 0.0679 |
| Step 3 | u₀ = (0.0649−0.0706)/0.0147 | −0.388 |
| Step 4 | |−0.388| vs 1.96 | 棄却できない |
🎯 試験で問われるポイント
パターン1:空欄補充
「修正不適合品率の式」「プール推定値」「標準誤差の式」などが空欄になる
パターン2:用語選択
「連続修正」「有限修正」「正規修正」などから正しい用語を選ぶ
パターン3:計算結果選択
検定統計量u₀の値を選択肢から選ぶ
① 連続修正の「+0.5」:離散→連続の近似精度向上
② 分母の「+1」:極端な値(0や1)を避ける
③ プール推定:H₀の下で2群を併合した推定値
④ 標準誤差:p*(1−p*)(1/nA+1/nB)の平方根
キーワード解説一覧(QC検定対策)
| 用語 | 意味・ポイント |
|---|---|
| 連続修正 (Yatesの修正) |
離散データ(計数値)を連続分布(正規分布)で近似するときのズレを補正する手法。±0.5の幅を考慮する。 |
| 修正不適合品率 p* |
p* = (x+0.5)/(n+1)。連続修正と極端な値の回避を両立した推定値。正規近似の精度を高める。 |
| プール推定 (併合推定) |
帰無仮説H₀(2群の母比率が等しい)の下で、2群のデータを合わせて共通の母比率を推定する方法。 |
| 標準誤差 | 推定量のばらつきの大きさ。検定統計量の分母に使う。SE = √[p*(1−p*)(1/nA+1/nB)] |
| 母比率の差の検定 | 2つの母集団の比率(不良率など)に統計的な差があるかを検定する手法。大標本ではZ検定を使う。 |
| 両側検定 | 対立仮説が「≠」(等しくない)の形。棄却域が分布の両端にある。α=0.05なら|u₀|>1.96で棄却。 |
| 帰無仮説 | 「差がない」「効果がない」という仮説。検定では、これを棄却できるかどうかを判断する。 |
| 正規分布近似 | 二項分布をnが大きいとき正規分布で近似すること。np≧5かつn(1−p)≧5が目安。 |
この記事のまとめ
- 連続修正:離散データを連続分布で近似するときの「階段→坂道」のズレを補正
- 修正不適合品率 p* = (x+0.5)/(n+1):分子の+0.5は連続修正、分母の+1は極端な値を避ける
- プール推定:帰無仮説の下で2群を併合し、共通の母比率を推定
- 検定統計量:u₀ = (p*A−p*B) / √[p*(1−p*)(1/nA+1/nB)]
- 判定:両側検定でα=0.05なら、|u₀|>1.96で帰無仮説を棄却
📚 次に読むべき記事
連続修正なしの基本版を学びたい方はこちら。基礎をしっかり固めましょう。
1つの母集団の比率を検定する方法。母比率の差の検定の前提知識です。
サンプルサイズが小さい場合は正規近似が使えません。その場合の検定方法を解説。
検定・推定を体系的に学びたい方はこちら。全体像から詳細まで網羅しています。