- 抜取検査で「二項分布」「超幾何分布」「ポアソン分布」が出てきて混乱する
- OC曲線って何を表しているのかイメージできない
- QC検定の穴埋め問題で、どの分布を選べばいいか迷ってしまう
- 抜取検査の「判定能力」とは何かをイメージで理解
- 二項分布・超幾何分布・ポアソン分布の使い分けルール
- OC曲線(検査特性曲線)の意味と読み方
「抜取検査の判定能力は、○○分布で計算し…」
QC検定でよく出るこの穴埋め問題、正直どれを選べばいいか迷いますよね。
でも安心してください。
実は、たった1つの判断基準を覚えれば、もう迷いません。
この記事では、抜取検査で使う確率分布の使い分けと、OC曲線の意味を中学生でもわかるように図解で徹底解説します。
目次
抜取検査の「判定能力」とは?
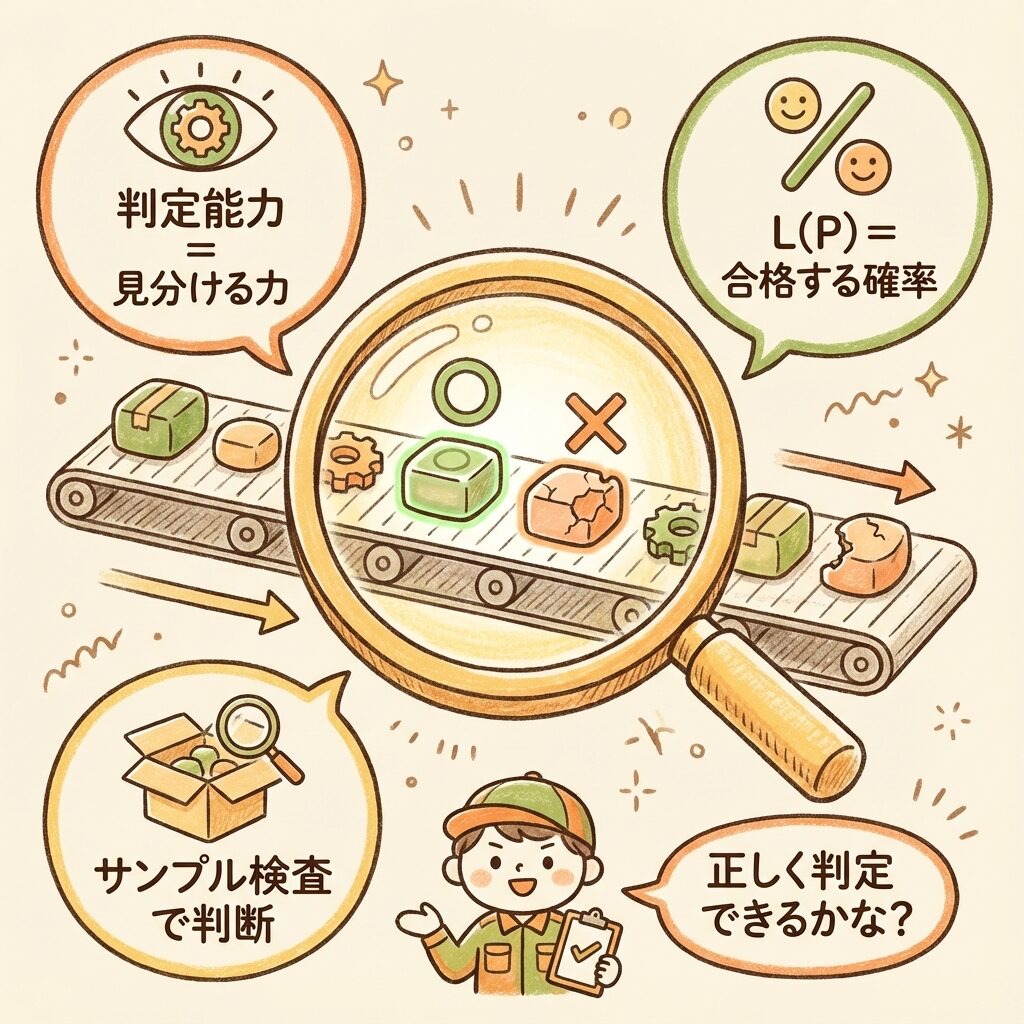
まず、「判定能力」という言葉の意味を押さえましょう。
判定能力 = 良いロットを「合格」、悪いロットを「不合格」と正しく判定できる力
抜取検査は、ロットの中から一部だけサンプルを取り出して検査します。
そのため、「本当は良いロットなのに不合格にしてしまう」「本当は悪いロットなのに合格にしてしまう」というミスが起こりえます。
このミスがどれくらい起こりやすいか(起こりにくいか)を表すのが「判定能力」です。
判定能力は「検査の目の良さ」のようなものです。
目が良ければ、良品と不良品を正確に見分けられます。
目が悪いと、見間違いが多くなります。
合格の確率 L(P) とは?
判定能力を数値で表すために使うのが「合格の確率 L(P)」です。
L(P) = ロットの不良率がPのとき、そのロットが「合格」と判定される確率
たとえば、不良率5%のロットを検査したとき、合格と判定される確率が90%なら、
L(0.05) = 0.90 と表します。
このL(P)を計算するために、確率分布を使います。
ここが今日のメインテーマです。
確率分布の使い分け|これがQC検定の頻出ポイント!
抜取検査でL(P)を計算するとき、3つの確率分布が登場します。
状況によって使い分けるルールを覚えましょう。
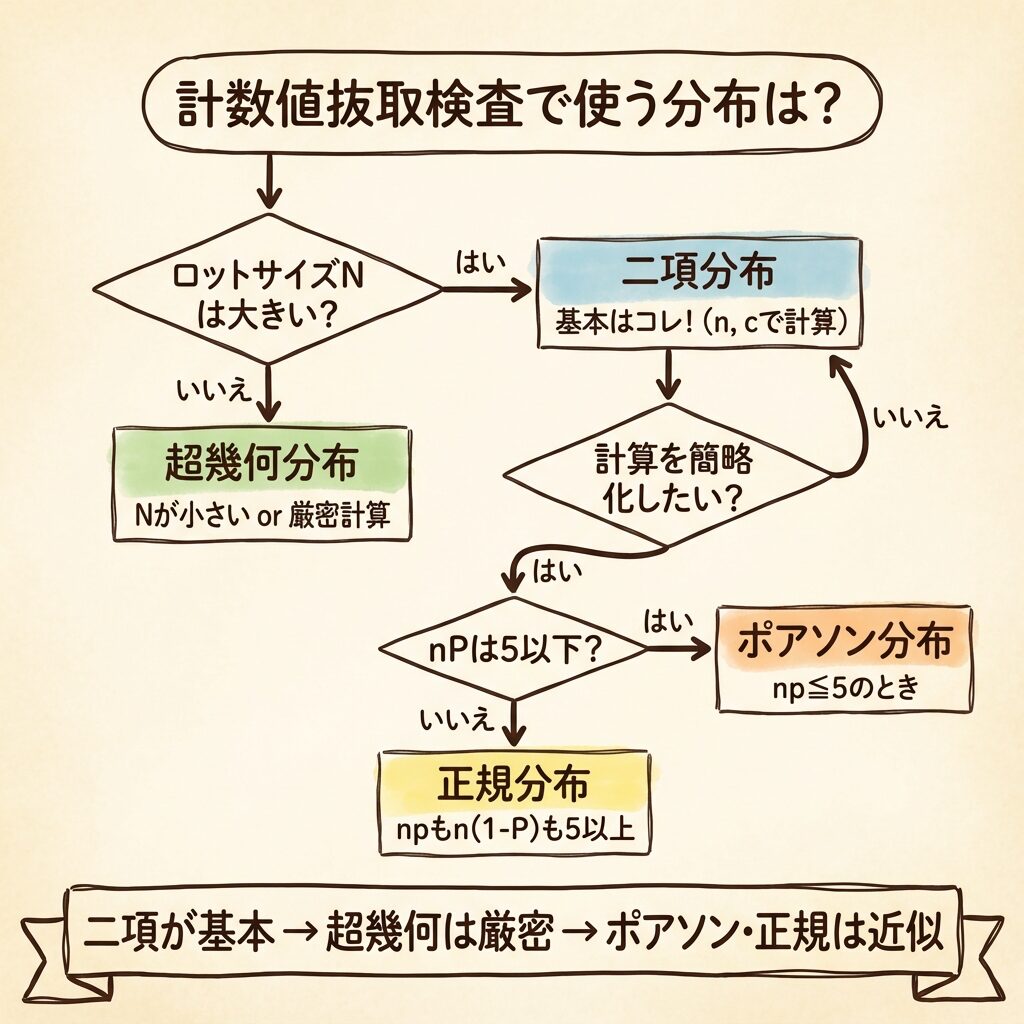
基本は「二項分布」で計算する
計数値抜取検査(不適合品の「数」で合否判定する検査)では、基本的に二項分布を使います。
二項分布は「n回試行して、成功がx回起こる確率」を計算する分布です。
抜取検査では:
・n個のサンプルを取り出す
・その中に不適合品がx個ある確率を求める
まさにピッタリの分布なんですね。
サンプルサイズをn、合格判定個数をcとすると、
「不適合品がc個以下のとき合格」なので、L(P)は次のように計算します。
n:サンプルサイズ、c:合格判定個数、P:ロットの不良率
第12回:二項分布とは?|コイン投げで理解する「成功回数」の確率分布 →
ロットサイズが小さい or 厳密に求めたい → 「超幾何分布」
ここが重要なポイントです。
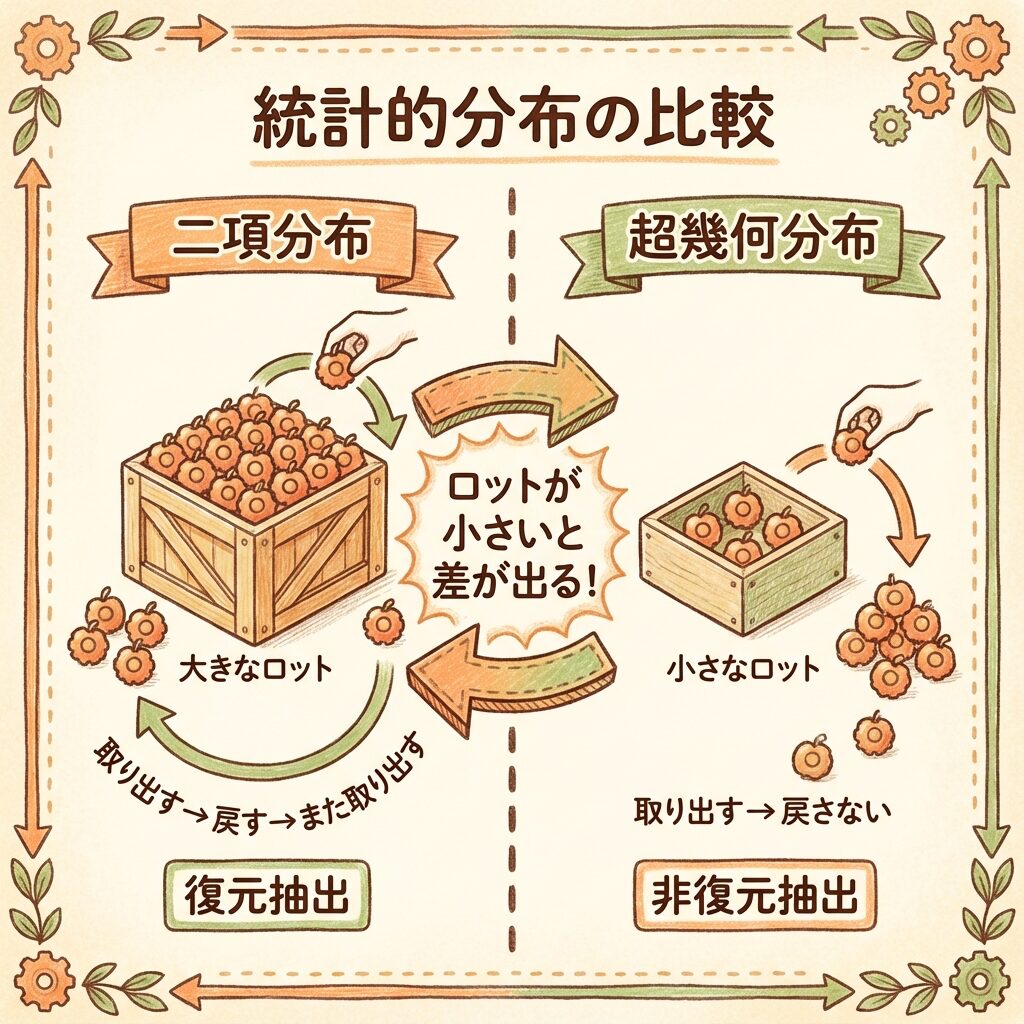
二項分布には「復元抽出」という前提があります。
つまり、「1個取り出して検査したら、また元に戻す」という想定です。
しかし、実際の抜取検査は「非復元抽出」(取り出したら戻さない)ですよね。
ロットサイズN(母集団の大きさ)が小さいと、
「復元抽出」と「非復元抽出」で確率が大きくズレます。
たとえば、100個のロットから50個取り出す場合、
1個目で不良品を引くと、2個目の不良率は変わってしまいます。
このようなケースでは、超幾何分布を使って厳密に計算します。
・ロットサイズNが小さい場合
・確率を厳密に求めたい場合
・「ロットサイズNを含めて」計算する場合
| 分布 | 抽出方法 | 使う場面 |
|---|---|---|
| 二項分布 | 復元抽出(独立試行) | 基本形・ロットが大きい場合 |
| 超幾何分布 | 非復元抽出 | ロットが小さい・厳密計算 |
従来の累積確率曲線 → 「ポアソン分布」または「正規分布」で近似
二項分布や超幾何分布は、正確な計算ができる反面、計算がとても面倒です。
特に、nが大きくなると組み合わせの計算(ₙCₓ)が爆発的に増えます。
電卓がなかった時代、これは大きな問題でした。
そこで、近似計算が使われてきました。
ポアソン分布で近似:
・nが大きく、Pが小さい場合(np ≤ 5程度)
・「めったに起きないこと」の確率計算に向く
正規分布で近似:
・nが十分大きく、npもn(1-P)も5以上の場合
・計算が最も簡単になる
「従来から用いられている累積確率曲線」というのは、この近似を使って作られたグラフのことです。
第13回:ポアソン分布とは?|「めったに起きないこと」を予測する魔法の道具 →
分布の使い分け|一覧表で整理
ここまでの内容を、一覧表で整理しましょう。
QC検定ではこの表の内容がそのまま出題されます。
| 条件 | 使う分布 | 特徴 |
|---|---|---|
| 基本形(n, cで計算) | 二項分布 | 独立試行の基本モデル |
| Nが小さい/厳密計算 | 超幾何分布 | 非復元抽出を考慮 |
| 近似(nが大、Pが小) | ポアソン分布 | 計算が簡略化できる |
| 近似(nが十分大) | 正規分布 | 最も計算が楽 |
「二項が基本、超幾何は厳密、ポアソン・正規は近似」
この流れを覚えておけば、穴埋め問題は完璧です!
OC曲線(検査特性曲線)とは?
さて、最後のキーワード「OC曲線」について解説します。
OC曲線 = ロットの品質と合格確率の関係を示すグラフ
OC曲線は「Operating Characteristic curve」の略で、日本語では「検査特性曲線」と呼びます。
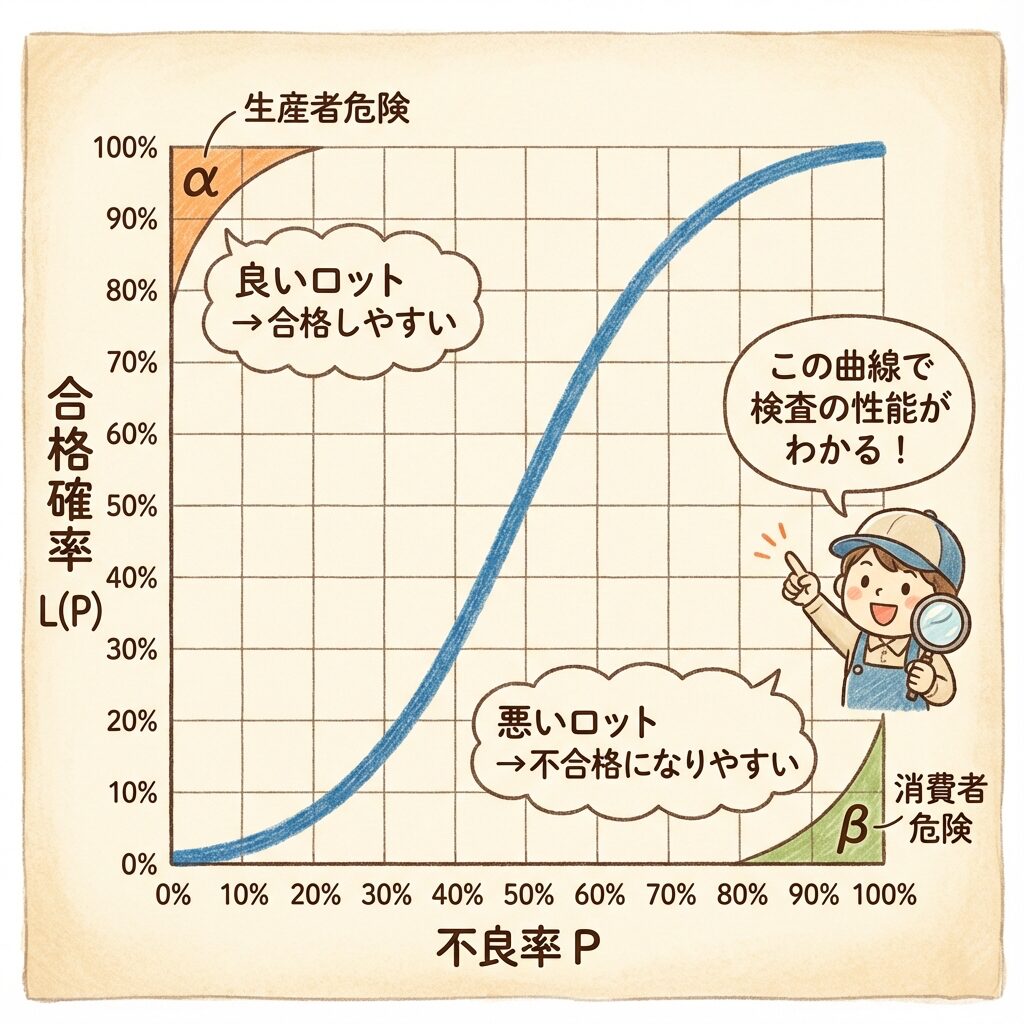
横軸:ロットの不良率 P
縦軸:合格の確率 L(P)
ロットの品質に対する合格確率の推移を曲線で示したもの
このグラフを見れば、「不良率がどれくらいのロットが、どれくらいの確率で合格するか」が一目でわかります。
OC曲線の形と意味
理想的なOC曲線と現実のOC曲線を比べてみましょう。
理想的なOC曲線
理想的には、「良いロット(P ≤ p₀)は100%合格、悪いロット(P > p₁)は100%不合格」となるべきです。
この場合、OC曲線は「階段状」になります。
現実のOC曲線
しかし、抜取検査では全数を見るわけではないので、どうしても誤判定のリスクがあります。
そのため、OC曲線は「なだらかなS字カーブ」になります。
| 不良率P | 合格確率L(P) | 意味 |
|---|---|---|
| P = 0%(完璧なロット) | L(P) = 100% | 必ず合格 |
| P = 小さい | L(P) = 高い | ほぼ合格 |
| P = 大きい | L(P) = 低い | ほぼ不合格 |
| P = 100%(全部不良) | L(P) = 0% | 必ず不合格 |
第6回:OC曲線の見方をマスター|抜取検査の性能が一目でわかるグラフの読み方 →
生産者危険(α)と消費者危険(β)
OC曲線を見ると、2種類のリスクが見えてきます。
| リスク | 記号 | 意味 | 誰が困る? |
|---|---|---|---|
| 生産者危険 | α | 良いロットが不合格になる確率 | 生産者(売り手) |
| 消費者危険 | β | 悪いロットが合格になる確率 | 消費者(買い手) |
生産者危険α:「あわてんぼう」の誤り
→ 良いものを「悪い!」と間違える(第1種の過誤)
消費者危険β:「ぼんやり者」の誤り
→ 悪いものを「良い」と見逃す(第2種の過誤)
練習問題で知識を確認しよう
ここまで学んだ知識を、練習問題で確認しましょう。
次の文章の【 】に入る最も適切な語句を、下の選択肢から選びなさい。
計数値抜取検査において、サンプル中の不適合品数の確率を求める際、サンプルサイズnと合格判定個数cがわかっている場合は【 ア 】分布を用いる。一方、ロットサイズNが小さく厳密な確率計算が必要な場合は【 イ 】分布を用いる。また、計算を簡略化するために【 ウ 】分布で近似することもある。これらの計算結果から、ロットの不良率と合格確率の関係をグラフ化したものを【 エ 】曲線と呼ぶ。
【選択肢】
①正規 ②二項 ③ポアソン ④超幾何 ⑤t ⑥OC ⑦AOQ ⑧管理
解答と解説
| 空欄 | 解答 | 選択肢 | 理由 |
|---|---|---|---|
| ア | 二項 | ② | n, cで計算する基本形 → 二項分布 |
| イ | 超幾何 | ④ | Nが小さい・厳密計算 → 超幾何分布 |
| ウ | ポアソン | ③ | 計算の簡略化 → ポアソン近似 |
| エ | OC | ⑥ | 品質vs合格確率のグラフ → OC曲線 |
「正規分布」も近似に使えることを知っておきましょう。
ただし、QC検定では「従来から用いられている」という文脈ではポアソン分布が正解になることが多いです。
また、「AOQ曲線」(平均出検品質曲線)という別の曲線もあるので、OC曲線と混同しないように注意!
まとめ
この記事では、抜取検査の判定能力とOC曲線について解説しました。
1. 判定能力 = 良いロットを合格、悪いロットを不合格と正しく判定できる力
2. 確率分布の使い分け
・基本形 → 二項分布
・Nが小さい/厳密計算 → 超幾何分布
・近似計算 → ポアソン分布(または正規分布)
3. OC曲線 = ロットの品質(不良率P)と合格確率L(P)の関係を示す曲線
「二項が基本、超幾何は厳密、ポアソンは近似」
この合言葉を覚えておけば、QC検定の穴埋め問題は怖くありません!
📚 次に読むべき記事
OC曲線の読み方を実際のグラフを使って詳しく解説します
α・βの意味と計算方法を具体例で理解できます
抜取検査を体系的に学びたい方はこちらの全体マップへ
