- 「因子負荷量」と「固有ベクトル」の違いがわからない
- 表を見ても、主成分が「何を意味しているか」が説明できない
- プラスとマイナスが混在していると、どう解釈すればいいか迷う
- 因子負荷量を「磁石の引き寄せ力」でイメージできる
- 因子負荷量の表から主成分の意味を読み取るコツがわかる
- QC検定1級の問題に自信を持って答えられる
目次
因子負荷量とは?|主成分と変数の「仲良し度」
主成分分析をすると、「第1主成分」「第2主成分」という新しい軸ができます。
でも、「この主成分は何を表しているの?」がわからないと、分析の意味がありませんよね。
そこで使うのが因子負荷量です。

因子負荷量 = 主成分と元の変数がどれくらい「仲良し」か(相関係数)
例えば、テストの成績で考えてみましょう。
「第1主成分」と「数学」の因子負荷量が0.85なら、「数学ができる人は第1主成分も高い傾向がある」という強い関係を意味します。
逆に因子負荷量が0.20なら、「ほとんど関係がない」ということです。
因子負荷量の範囲|-1から+1まで
因子負荷量は相関係数と同じで、-1から+1の範囲の値をとります。
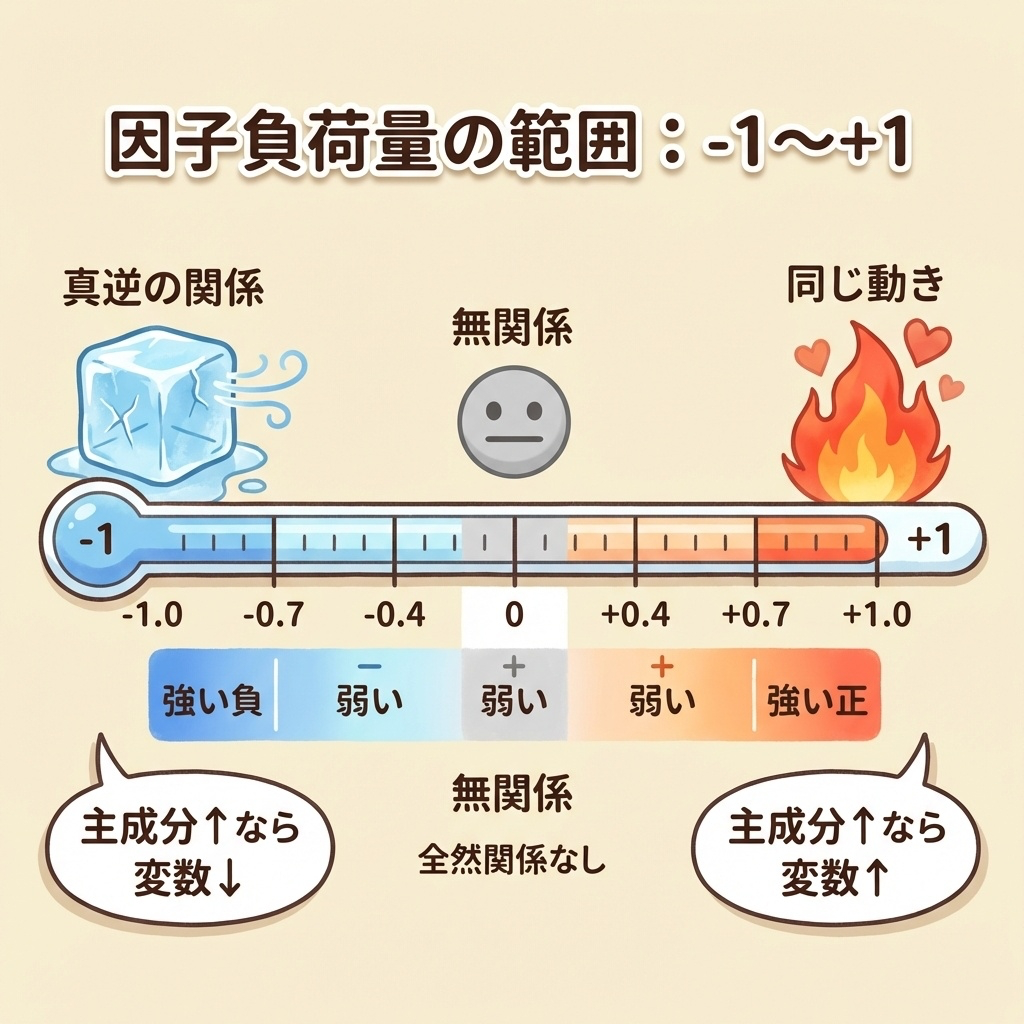
| 因子負荷量 | 意味 | イメージ |
|---|---|---|
| +1に近い | 主成分が上がると、変数も上がる | 🤝 親友レベル |
| 0に近い | ほとんど関係がない | 😐 他人 |
| -1に近い | 主成分が上がると、変数は下がる | 🔄 真逆の動き |
磁石で理解する因子負荷量|引き寄せられる強さ
因子負荷量を理解する最強のたとえは「磁石」です。
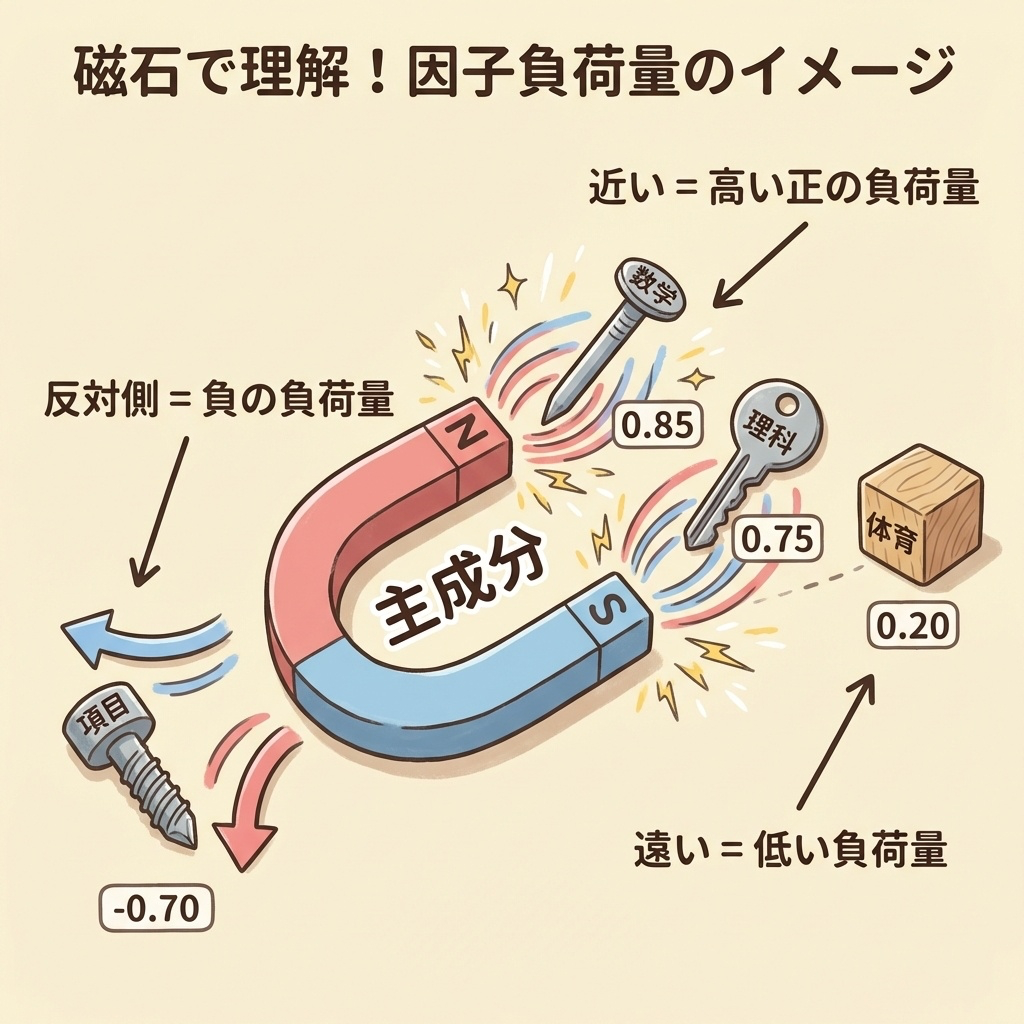
「第1主成分」という磁石があるとします。
周りには「数学」「国語」「体育」などの変数が浮いています。
- 🧲⬅️📐 数学は磁石に強く引き寄せられている(因子負荷量 0.85)
- 🧲⬅️📖 国語もそこそこ引き寄せられている(因子負荷量 0.70)
- 🧲 ⚽ 体育はほとんど引き寄せられていない(因子負荷量 0.15)
磁石に近いものほど、その主成分と強い関係があるのです!
さらに、磁石にはN極とS極がありますよね。
因子負荷量がプラスの変数はN極側に引き寄せられ、マイナスの変数はS極側に引き寄せられます。これが「正の関係」と「負の関係」の違いです。
因子負荷量の公式|なぜ√固有値をかけるの?
因子負荷量の計算式を見てみましょう。

| 固有ベクトル | 主成分の方向を決める係数(前回学んだ「コンパス」) |
| √固有値 | 主成分の重要度を反映する数値(前回学んだ「宝の量」の平方根) |
なぜ√固有値をかけるの?|重要度を反映させるため
固有ベクトルだけだと、すべての主成分が「同じ長さ」になってしまいます。
でも実際は、第1主成分のほうが第2主成分より重要ですよね。
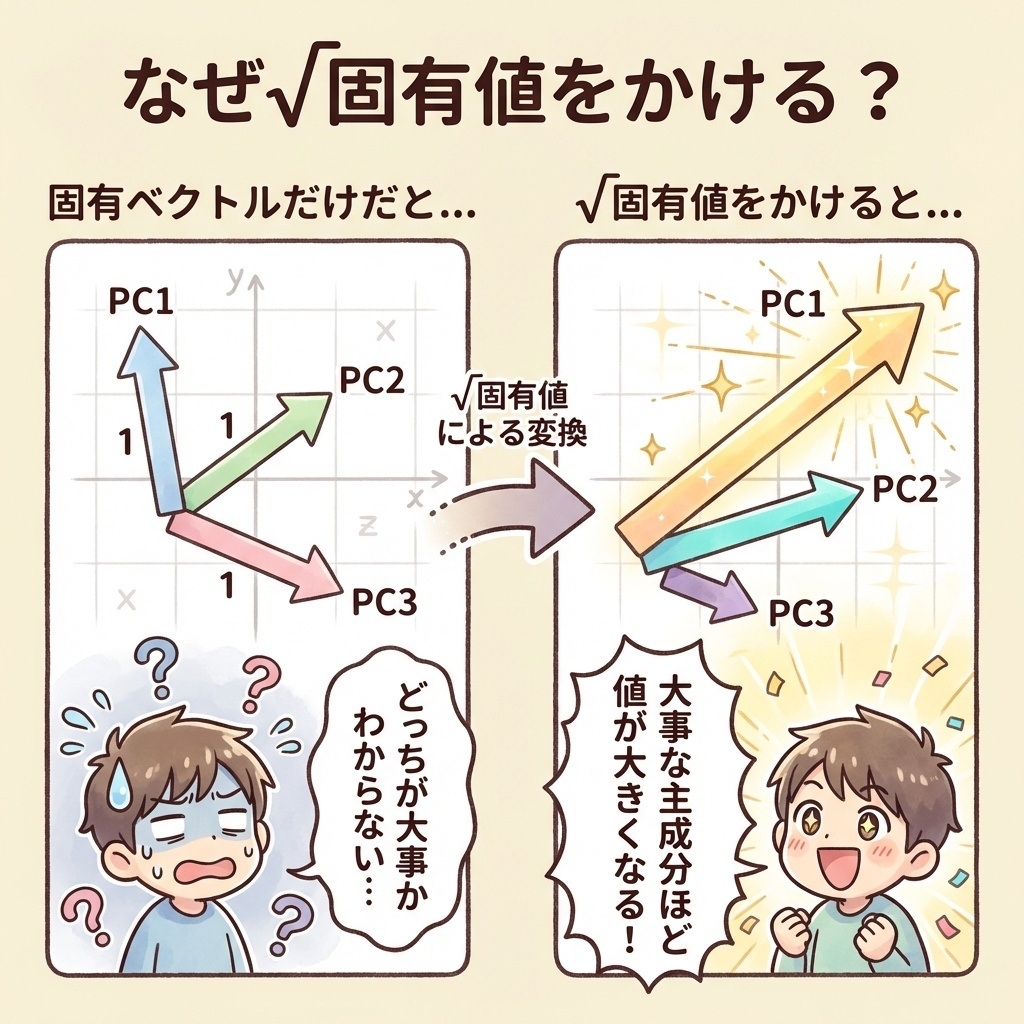
固有値が大きい主成分ほど、因子負荷量も大きくなる。
これによって「重要な主成分ほど、変数との関係が強く見える」ようになります。
計算例|実際に数字を入れてみよう
与えられた情報:
- 第1主成分の固有値:λ₁ = 2.1
- 数学の固有ベクトル成分:0.58
計算:
因子負荷量 = 0.58 × √2.1
= 0.58 × 1.45
= 0.84
結果:数学と第1主成分の因子負荷量は0.84(とても強い関係!)
統計ソフトは因子負荷量を自動計算してくれます。
試験では「因子負荷量の表を読み取る」問題が中心なので、計算より解釈を重視しましょう!
因子負荷量の表の読み方|主成分の「意味」を見抜く
因子負荷量の最大の目的は、「主成分が何を意味しているか」を理解することです。
実際の表を見てみましょう。

| 変数 | PC1 | PC2 |
|---|---|---|
| 数学 | 0.85 ⭐ | 0.45 |
| 理科 | 0.82 ⭐ | 0.40 |
| 国語 | 0.75 ⭐ | -0.60 ❄️ |
| 社会 | 0.70 ⭐ | -0.65 ❄️ |
⭐ = 高いプラスの値 ❄️ = 高いマイナスの値
この表から何がわかる?
すべての科目が0.7以上のプラスで高い
→ 数学も、理科も、国語も、社会も関係している
→ PC1 = 「総合学力」を表している!
数学・理科はプラス(+0.4〜0.45)
国語・社会はマイナス(-0.60〜-0.65)
→ 理系科目と文系科目が逆の動きをする
→ PC2 = 「理系 vs 文系」のバランスを表している!
主成分を解釈する3ステップ|名探偵になろう
因子負荷量の表から主成分の意味を読み取るには、3つのステップがあります。

まず、因子負荷量の絶対値が0.7以上のセルを見つけます。
(プラスでもマイナスでも、数字の大きさで判断!)
これが「その主成分に強く関係している変数」です。

Step 1で見つけた変数に共通するテーマを探します。
例:「数学、理科、国語、社会」→ 共通点は「勉強の科目」
例:「寸法A、寸法B、重量」→ 共通点は「サイズに関係する項目」

共通点から、主成分にわかりやすい名前をつけます。
コツ:
・全部プラスで高い → 「総合〇〇」「全体〇〇」
・プラスとマイナスが混在 → 「〇〇 vs △△」
3つのパターンを覚えよう|これで解釈は完璧!
因子負荷量の表には、大きく分けて3つのパターンがあります。
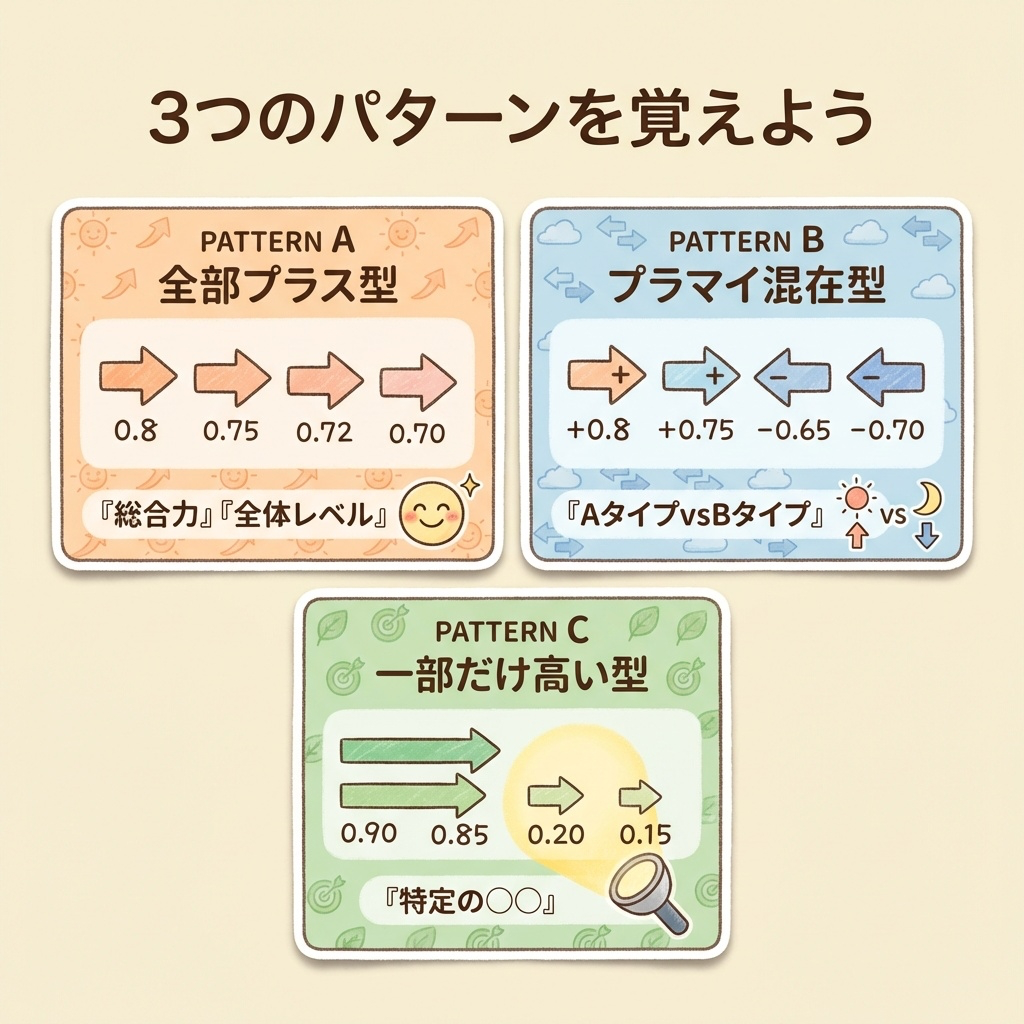
| パターン | 因子負荷量の特徴 | 主成分の意味 | 名前の例 |
|---|---|---|---|
| ①全部プラス型 | すべての変数がプラスで高い | 全体のレベル | 「総合力」「全体サイズ」 |
| ②プラマイ混在型 | プラスとマイナスが混在 | 2つのグループの対比 | 「理系vs文系」「硬さvs柔らかさ」 |
| ③一部だけ高い型 | 特定の変数だけ高い | 特定の特性 | 「表面品質」「材料特性」 |
実例:製造業の品質データ|実務で使えるようになろう
製造業の品質管理でも、因子負荷量は大活躍します。
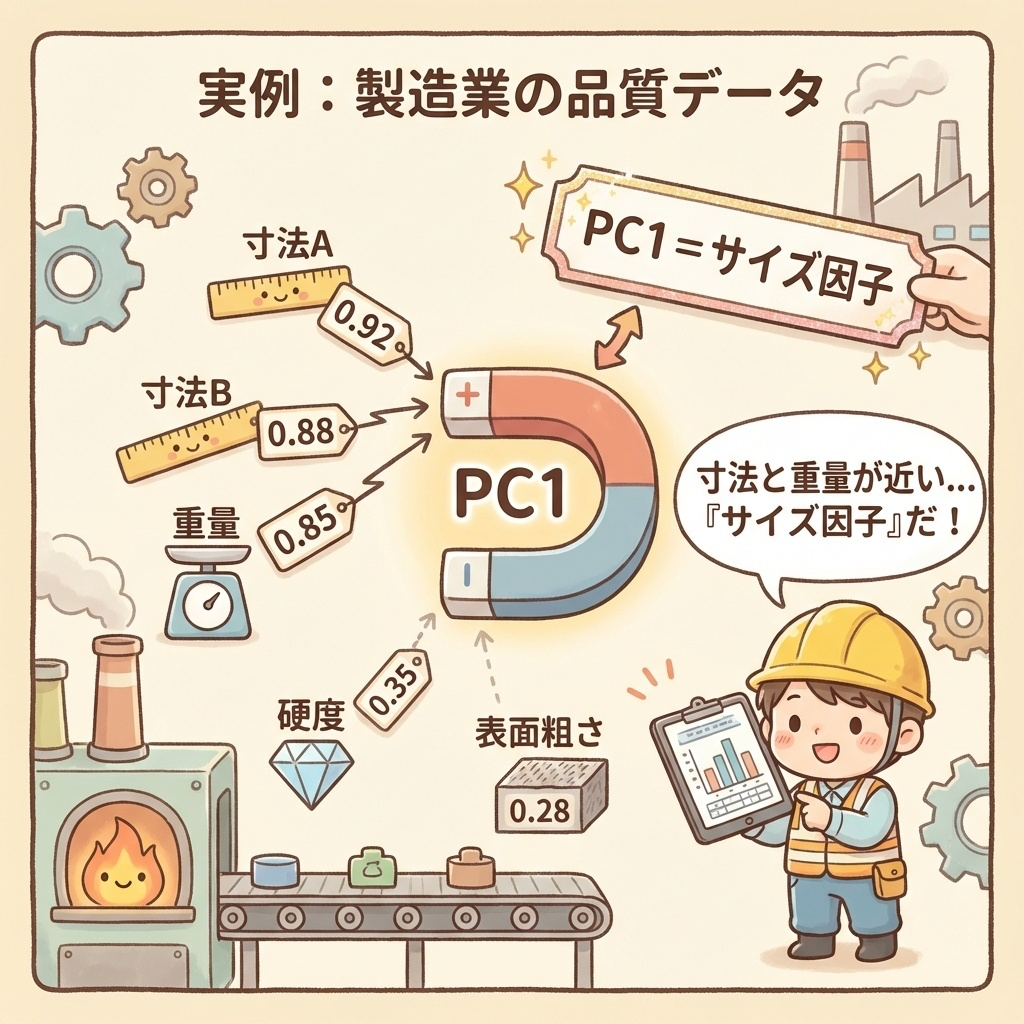
測定項目:寸法A、寸法B、重量、硬度、表面粗さ
| 変数 | PC1 | PC2 |
|---|---|---|
| 寸法A | 0.92 | 0.15 |
| 寸法B | 0.88 | 0.20 |
| 重量 | 0.85 | 0.25 |
| 硬度 | 0.35 | 0.91 |
| 表面粗さ | 0.28 | 0.87 |
解釈:
- PC1:寸法A、寸法B、重量が高い → 「サイズ因子」
- PC2:硬度、表面粗さが高い → 「材料特性因子」
因子負荷量プロット(バイプロット)の読み方
因子負荷量は、グラフ(プロット)で視覚化されることもあります。
これを「バイプロット(Biplot)」といいます。

PC1を横軸、PC2を縦軸にして、各変数を矢印で表示したグラフです。
矢印の長さ・方向・角度から、因子負荷量の情報が読み取れます。
バイプロットの読み方|3つのポイント
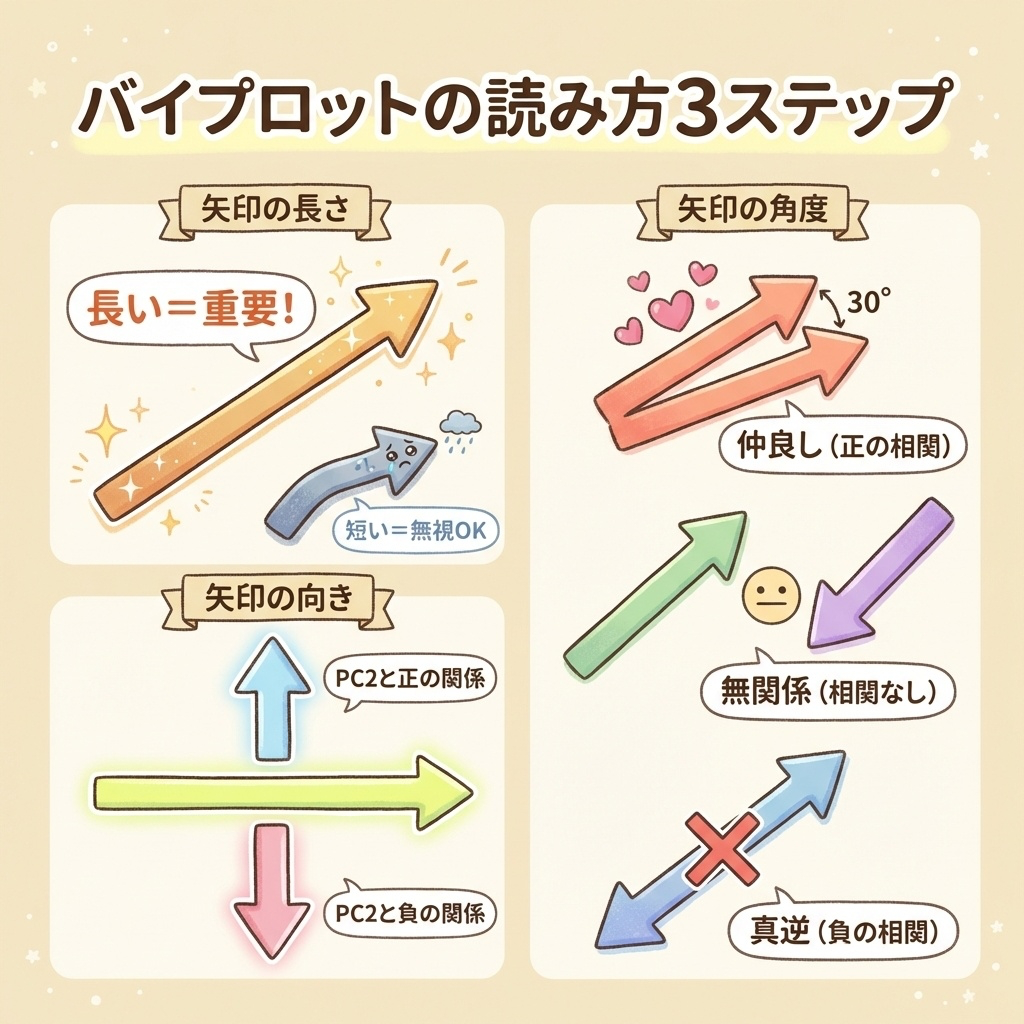
| 見るポイント | 意味 | 具体例 |
|---|---|---|
| ①矢印の長さ | 主成分にとっての重要度 | 長い矢印 = 重要な変数 |
| ②矢印の方向 | どの主成分と関係するか | 右向き = PC1と正の関係 上向き = PC2と正の関係 |
| ③矢印同士の角度 | 変数間の相関 | 近い = 正の相関 90° = 無相関 180° = 負の相関 |
①まず長い矢印を探す(重要な変数)
②次に似た方向の矢印をグループ化する
③グループの共通点から主成分の意味を解釈する
因子負荷量の判断基準|これだけ覚えればOK!
| 絶対値 | 関係の強さ | 解釈での扱い |
|---|---|---|
| 0.7以上 | 強い ⭐ | 主成分の意味を決める重要な変数 |
| 0.4〜0.7 | 中程度 | ある程度関係があるが、主役ではない |
| 0.4未満 | 弱い | ほとんど無視してOK |
まとめ|因子負荷量を完全マスター!

| 項目 | 内容 |
|---|---|
| 因子負荷量とは | 主成分と変数の「仲良し度」(相関係数) |
| 範囲 | -1 ~ +1 |
| 公式 | 固有ベクトル × √固有値 |
| 判断基準 | |0.7以上| = 強い関係 → 解釈に使う |
| 解釈の3ステップ | ①0.7以上を探す → ②共通点を見つける → ③名前をつける |
- 因子負荷量 = 磁石の引き寄せ力(近いほど強い関係)
- |0.7以上| の変数を探すのが解釈のスタート
- 全部プラス = 「総合〇〇」、プラマイ混在 = 「〇〇 vs △△」
- バイプロットは矢印の長さ・方向・角度で読む
📚 次に読むべき記事
因子負荷量の次は「主成分得点」!各データの新しい成績表を計算する方法を解説。
固有値・寄与率を復習したい方はこちら。因子負荷量と合わせて理解を深めよう。
主成分分析の全体像と「何のためにやるのか」を確認したい方はこちら。
【完全版】統計学の勉強ロードマップ|初心者が「データ分析」を武器にするまでの全手順 →
