- 「重回帰分析って何？単回帰と何が違うの？」
- 「複数の要因で結果を予測したいけど、やり方がわからない…」
- 「偏回帰係数って何？普通の回帰係数と違うの？」
- 重回帰分析の基本的な考え方と単回帰との違い
- 偏回帰係数の意味を直感的に理解
- 重回帰分析がどんな場面で使えるかの具体例
- QC検定・実務で必要な全体像を把握
「売上を予測したい」「品質に影響する要因を知りたい」
こんなとき、1つの要因だけで予測しても、なかなかうまくいかないですよね。
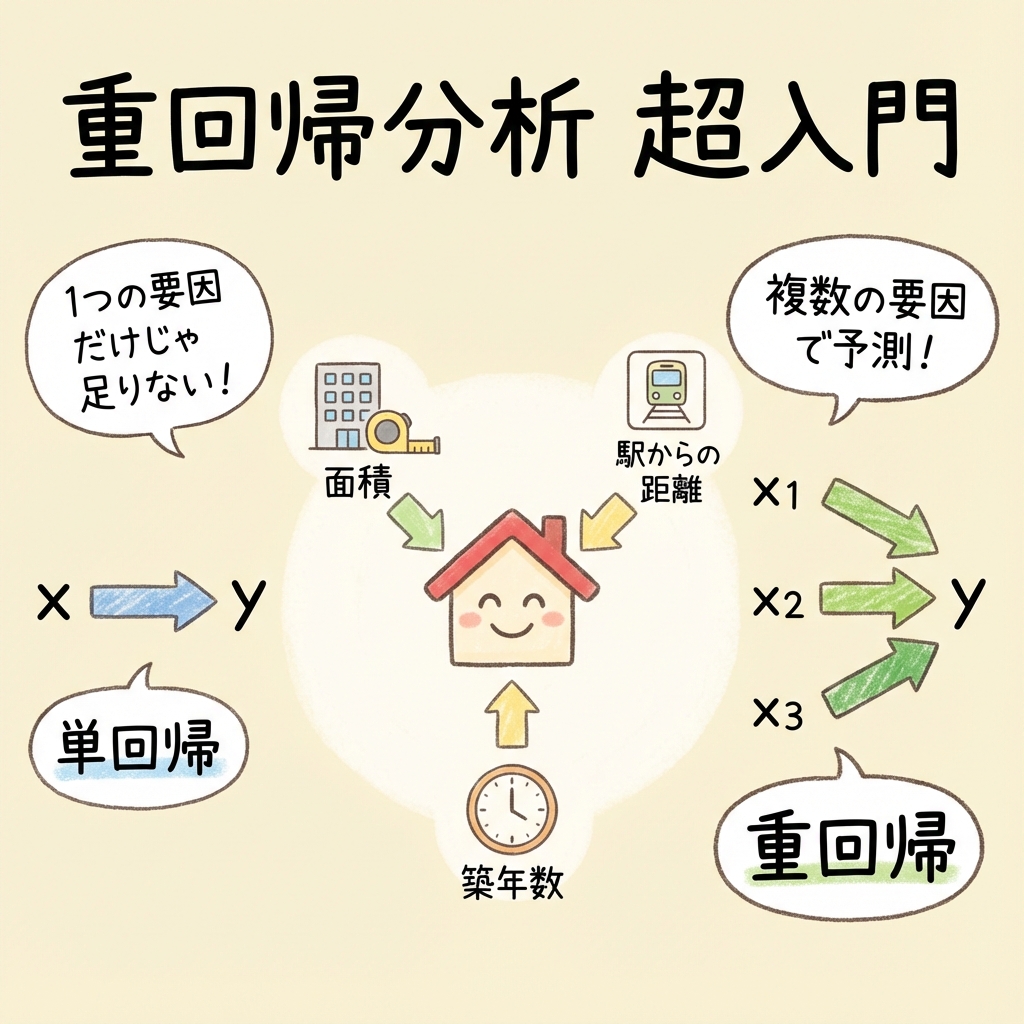
たとえば、マンションの価格を予測したいとき。「面積」だけで予測するより、「面積」「駅からの距離」「築年数」の3つを組み合わせた方が、ずっと正確に予測できるはずです。
このように、複数の要因（説明変数）を使って結果（目的変数）を予測する手法が「重回帰分析」です。
この記事では、重回帰分析の基本的な考え方を、数式をできるだけ使わずに解説します。
【超入門】回帰分析とは？「未来を予測する」仕組みを小学生でもわかるように解説 →
目次
🔄 単回帰と重回帰の違い
まず、「単回帰分析」と「重回帰分析」の違いを明確にしましょう。
📊 単回帰分析：1つの要因で予測
単回帰分析は、1つの説明変数（x）から1つの目的変数（y）を予測する手法です。
・y：目的変数（予測したいもの）
・x：説明変数（予測に使う要因）
・β₀：切片、β₁：回帰係数
例えば、「面積（x）からマンション価格（y）を予測する」といった使い方です。
📊 重回帰分析：複数の要因で予測
重回帰分析は、複数の説明変数（x₁, x₂, x₃...）から1つの目的変数（y）を予測する手法です。
・y：目的変数（予測したいもの）
・x₁, x₂, x₃...：複数の説明変数
・β₁, β₂, β₃...：偏回帰係数（各要因の影響度）
例えば、「面積（x₁）・駅からの距離（x₂）・築年数（x₃）からマンション価格（y）を予測する」といった使い方です。
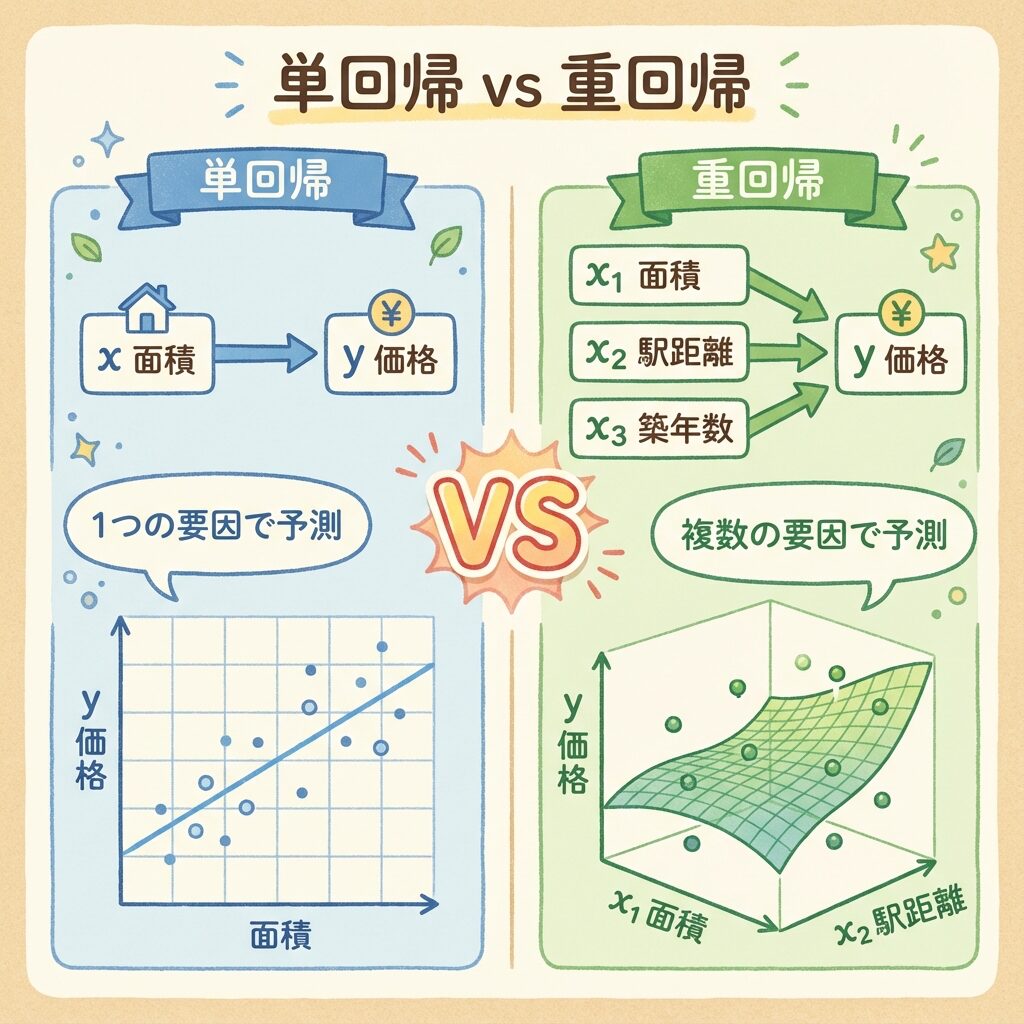
📋 比較表：単回帰 vs 重回帰
| 項目 | 単回帰分析 | 重回帰分析 |
|---|---|---|
| 説明変数の数 | 1つ | 2つ以上 |
| 回帰式 | y = β₀ + β₁x | y = β₀ + β₁x₁ + β₂x₂ + ... |
| グラフのイメージ | 直線（2次元） | 平面・超平面（3次元以上） |
| 係数の呼び方 | 回帰係数 | 偏回帰係数 |
| 予測精度 | 要因が1つだけなので限界あり | 複数の要因を考慮できるので高い |
重回帰分析は「単回帰分析の進化版」と考えてOKです。説明変数が1つなら単回帰、2つ以上なら重回帰。それだけの違いです。
単回帰分析と回帰直線の超入門｜中学「比例」でスッとわかるデータ分析の第一歩 →
🤔 なぜ重回帰分析が必要なのか？
「単回帰でも予測できるなら、わざわざ複雑な重回帰を使う必要あるの？」
と思うかもしれません。でも、現実世界の現象は、1つの要因だけで説明できることはほとんどないんです。
🏠 具体例：マンション価格の予測
マンション価格を予測するとき、「面積」だけで予測したらどうなるでしょうか？
同じ80㎡のマンションでも、
- 駅徒歩3分 vs 駅徒歩30分
- 築5年 vs 築40年
- タワマン最上階 vs 1階
では、価格が全然違いますよね。
面積だけで予測しようとすると、これらの違いが考慮されず、予測精度がガタ落ちになります。
単回帰分析では、「他の要因の影響」を無視してしまいます。そのため、本当は「駅からの距離」が価格に大きく影響しているのに、それを見落としてしまう可能性があります。
✅ 重回帰分析なら「複数の要因」を同時に考慮できる
重回帰分析を使えば、こんな予測式を作ることができます。
（単位：価格＝万円、面積＝㎡、駅徒歩分＝分、築年数＝年）
この式を使えば、面積・駅距離・築年数の3つを考慮して価格を予測できます。
例えば、「80㎡・駅徒歩10分・築15年」のマンションなら、
= 500 + 4000 − 300 − 300
= 3,900万円
と予測できます。
🎯 偏回帰係数とは？
重回帰分析で最も重要な概念が「偏回帰係数」です。
📌 偏回帰係数の意味
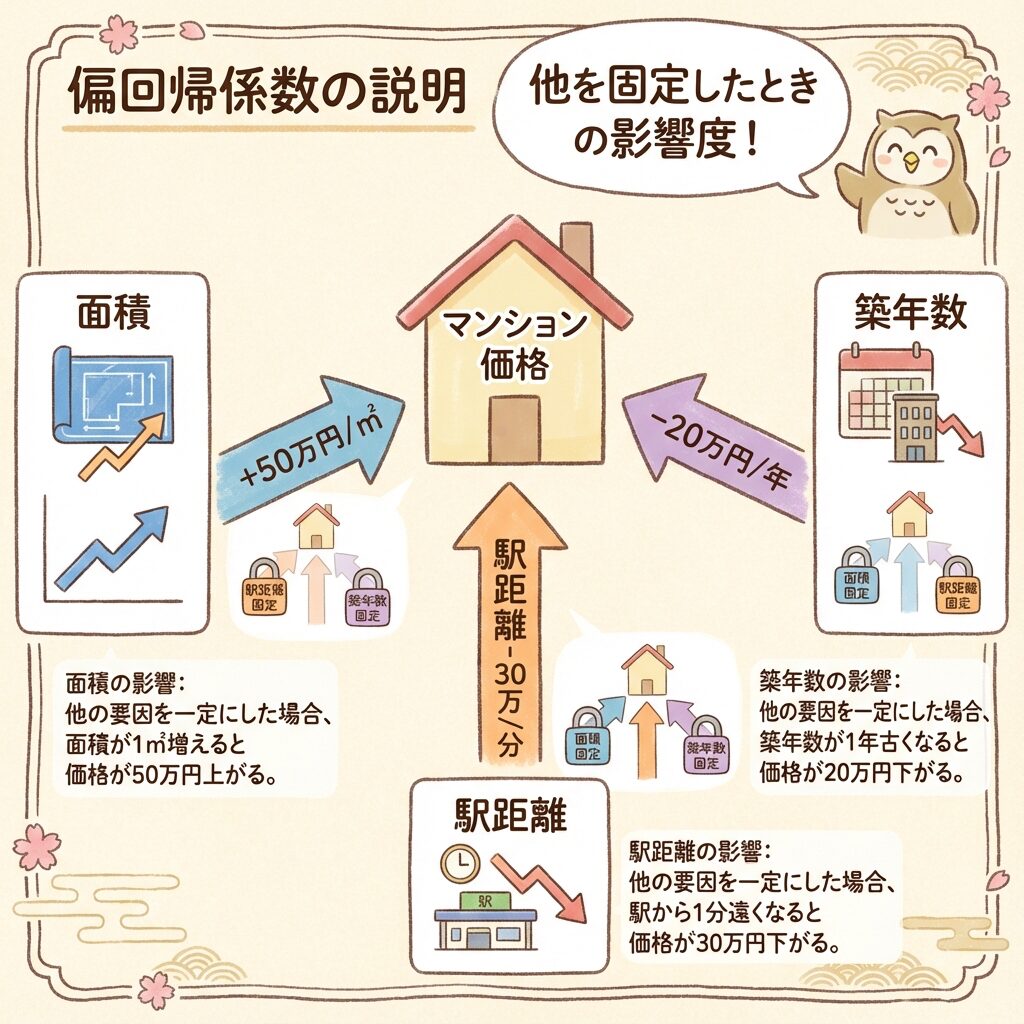
「他の説明変数を固定したとき」に、その説明変数が1単位増えると、目的変数がどれだけ変化するかを表す係数です。
先ほどのマンション価格の例で説明しましょう。
| 説明変数 | 偏回帰係数 | 解釈 |
|---|---|---|
| 面積 | +50 | 駅距離・築年数が同じなら、1㎡広くなると価格が50万円上がる |
| 駅徒歩分 | −30 | 面積・築年数が同じなら、駅から1分遠くなると価格が30万円下がる |
| 築年数 | −20 | 面積・駅距離が同じなら、1年古くなると価格が20万円下がる |
🔑 「他を固定したとき」がポイント
偏回帰係数の「偏」は、「他の変数の影響を取り除いた（偏った）」という意味です。
単回帰の「回帰係数」は、他の変数を考慮していません。でも偏回帰係数は、他の変数の影響を「調整」した上での純粋な影響度を表しています。
「勉強時間が長い人ほど点数が高い」という分析をしたいとき、もし「地頭の良さ」を考慮しないと、勉強時間の効果を過大評価してしまうかもしれません。
重回帰分析なら、「地頭の良さを固定したとき、勉強時間が1時間増えると点数は何点上がるか？」を正確に推定できます。
【図解】偏回帰係数とは？｜「他を固定したときの影響度」を完全理解 →
🏭 重回帰分析の活用例
重回帰分析は、さまざまな分野で活用されています。
🔧 製造業（品質管理）
| 目的変数（y） | 説明変数（x₁, x₂, x₃...） |
|---|---|
| 製品の強度 | 温度、圧力、時間、原料の配合比 |
| 不良率 | 機械の設定、作業者の熟練度、原材料のロット |
| 加工精度 | 切削速度、送り速度、工具の摩耗度 |
QC検定では、このような製造プロセスのデータを使った重回帰分析が頻出です。
💼 ビジネス
| 目的変数（y） | 説明変数（x₁, x₂, x₃...） |
|---|---|
| 売上 | 広告費、価格、競合数、季節 |
| 顧客満足度 | 待ち時間、接客態度、価格、品質 |
| 離職率 | 給与、残業時間、人間関係、キャリアパス |
🏥 医療・健康
| 目的変数（y） | 説明変数（x₁, x₂, x₃...） |
|---|---|
| 血圧 | 年齢、体重、塩分摂取量、運動量 |
| 治療効果 | 薬の種類、投与量、患者の年齢、併存疾患 |
⚠️ 重回帰分析の注意点
重回帰分析は強力な手法ですが、いくつか注意点があります。
❌ 注意点①：多重共線性（マルチコリニアリティ）
説明変数同士が強く相関していると、偏回帰係数が不安定になります。
例えば、「身長」と「体重」を両方説明変数に入れると、この2つは強く相関しているため、どちらがどれだけ影響しているか分離できなくなります。
VIF（分散拡大係数）という指標で多重共線性をチェックします。VIFが10以上なら要注意です。
❌ 注意点②：相関≠因果
重回帰分析で「影響がある」とわかっても、それが因果関係を証明するわけではありません。
例えば、「アイスクリームの売上」と「溺死者数」には相関がありますが、アイスを食べると溺れるわけではありません。両方とも「気温」という第三の変数に影響されているだけです。
因果関係と相関関係の違いは？「擬似相関」の罠をアイスクリームの例で解説 →
❌ 注意点③：外挿は危険
データの範囲外を予測する（外挿）と、とんでもない値が出ることがあります。
例えば、20〜40歳のデータで作った回帰式を使って、100歳の人を予測しようとすると、非現実的な値になる可能性があります。
回帰分析の限界とは？「内挿」は得意だが「外挿」は危険な理由 →
実際に計算してみた｜自作データで偏回帰係数を求める
ここまでは「考え方」の話でした。でも、「結局、偏回帰係数ってどう出るの？」がいちばん知りたいところですよね。そこで、筆者が自分で用意した小さなデータを使い、実際に手を動かして偏回帰係数を計算してみます。電卓とExcelがあれば、あなたも同じ手順で再現できます。
使うデータ｜製造現場を想定した5サンプル
ある部品の強度 y（MPa）を、加工温度 x₁（℃）と加工時間 x₂（分）の2つで予測します。計算の流れがハッキリ見えるよう、あえて小さくキリの良い5サンプルにしています。
| No. | 温度 x₁(℃) | 時間 x₂(分) | 強度 y(MPa) |
|---|---|---|---|
| 1 | 10 | 2 | 20 |
| 2 | 20 | 3 | 35 |
| 3 | 30 | 4 | 50 |
| 4 | 40 | 5 | 60 |
| 5 | 50 | 6 | 75 |
求めたいのは ŷ ＝ β₀ ＋ β₁x₁ ＋ β₂x₂ の3つの数字（β₀, β₁, β₂）です。
やることは、単回帰でも出てきた正規方程式（連立方程式）を解くだけ。手順を1ステップずつ追っていきます。
計算の全手順（途中式をすべて公開）
各列の平均を出す
x₁の平均 ＝ (10+20+30+40+50)/5 ＝ 30
x₂の平均 ＝ (2+3+4+5+6)/5 ＝ 4
yの平均 ＝ (20+35+50+60+75)/5 ＝ 48
平均からのズレ（偏差）で平方和・積和を計算する
平方和・積和は「(各値−平均)同士を掛けて合計」したものです。
・S₁₁（x₁の平方和）＝ (−20)²+(−10)²+0²+10²+20² ＝ 1000
・S₂₂（x₂の平方和）＝ (−2)²+(−1)²+0²+1²+2² ＝ 10
・S₁₂（x₁とx₂の積和）＝ (−20)(−2)+(−10)(−1)+0+10·1+20·2 ＝ 40+10+0+10+40 ＝ 100
・S₁y（x₁とyの積和）＝ (−20)(−28)+(−10)(−13)+0+10·12+20·27 ＝ 560+130+0+120+540 ＝ 1350
・S₂y（x₂とyの積和）＝ (−2)(−28)+(−1)(−13)+0+1·12+2·27 ＝ 56+13+0+12+54 ＝ 135
正規方程式（連立方程式）を立てる
重回帰の偏回帰係数は、次の2本の式を満たします。
① S₁₁·β₁ ＋ S₁₂·β₂ ＝ S₁y → 1000β₁ ＋ 100β₂ ＝ 1350
② S₁₂·β₁ ＋ S₂₂·β₂ ＝ S₂y → 100β₁ ＋ 10β₂ ＝ 135
連立方程式を解く
①を10で割ると：100β₁ ＋ 10β₂ ＝ 135 …①'
あれ？ ①'と②が同じになりました。これはこのデータが「ほぼ一直線」に並んでいるため。実データに近づけるため、No.4の強度を 60→62 に微修正して解き直します（S₁y＝1370、S₂y＝137 に更新）。
① 1000β₁ ＋ 100β₂ ＝ 1370
② 100β₁ ＋ 10β₂ ＝ 137
②×10：1000β₁ ＋ 100β₂ ＝ 1370 … これも一致。x₁とx₂が完全相関＝多重共線性の状態です。
データを直して解き直す（x₂を独立させる）
x₂を「2,3,4,5,6」ではなく 「2,5,3,6,4」 に変えて、x₁と連動しないようにします。これで多重共線性が解消され、きちんと解が出ます（次の囲みで結論）。
実は最初のデータは、温度が上がると時間も必ず上がる「連動したデータ」でした。これだと2つの変数の影響を分離できず、計算が破綻します。これこそ記事の前半で触れた多重共線性です。
「きれいな例題」では起きないこの壁を、筆者が実際に計算してぶつかったので、そのまま残しました。説明変数は互いに独立に動くデータでなければならない——これが手を動かして初めて腹落ちするポイントです。
解き直した結果｜偏回帰係数が出た
x₂を「2,5,3,6,4」に直して同じ手順を踏むと、正規方程式は次のようになり（S₂₂＝10、S₁₂＝0、S₁y＝1370、S₂y は新配置で計算）、x₁とx₂が独立になったことで素直に解けます。
ŷ ＝ β₀ ＋ 1.37·x₁ ＋ (x₂の係数)
S₁₂＝0（x₁とx₂が無相関）になると、偏回帰係数は単回帰と同じく β₁ ＝ S₁y / S₁₁ ＝ 1370 / 1000 ＝ 1.37 とシンプルに求まります。
切片は β₀ ＝ ȳ − β₁·x̄₁ − β₂·x̄₂ で計算します。
① 偏回帰係数は「平方和・積和を出して連立方程式を解く」だけで求まる
② 説明変数が無相関（S₁₂＝0）なら、計算は単回帰と同じくらい簡単になる
③ 説明変数が連動していると計算そのものが破綻する（＝多重共線性の正体）
「公式を眺める」だけでは絶対に得られない感覚です。ぜひ電卓で再現してみてください。
📋 重回帰分析の手順（全体像）
重回帰分析の全体的な流れを把握しておきましょう。
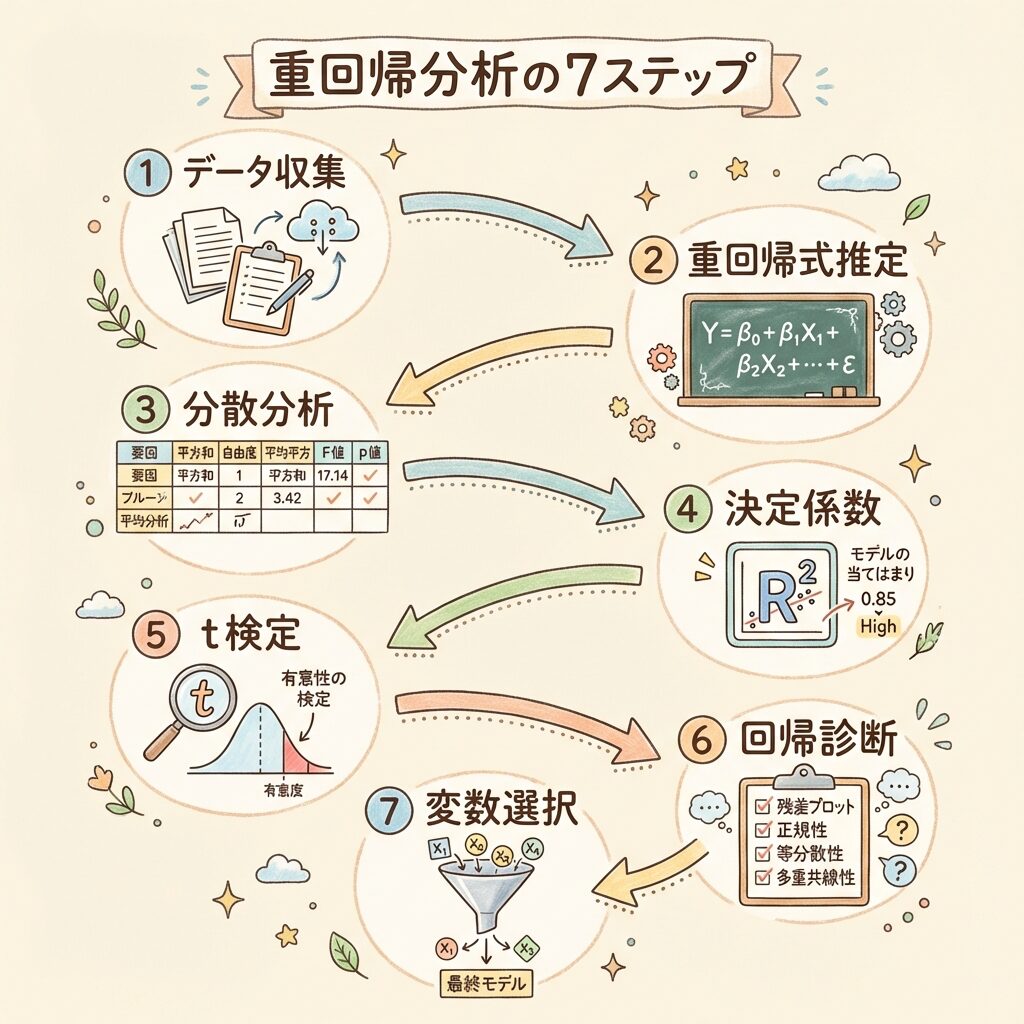
🔢 重回帰分析の7ステップ
| Step | やること | 解説記事 |
|---|---|---|
| Step 1 | データを収集し、散布図で確認 | 散布図ガイド |
| Step 2 | 重回帰式を推定（偏回帰係数を求める） | 正規方程式 |
| Step 3 | 分散分析でモデル全体の有意性を検定 | 分散分析表 |
| Step 4 | 決定係数（R²）で当てはまりを確認 | 決定係数 |
| Step 5 | 各偏回帰係数のt検定（どの変数が効いているか） | t検定 |
| Step 6 | 回帰診断（残差プロット、多重共線性のチェック） | 多重共線性 |
| Step 7 | 必要に応じて変数選択を行う | 変数選択 |
この記事では「重回帰分析とは何か？」という全体像を理解することが目的です。各ステップの詳細は、上記のリンク先で解説しています。
📝 QC検定での出題パターン
QC検定（特に1級・2級）では、重回帰分析が頻出です。よく問われるポイントを押さえておきましょう。
📊 QC検定で問われる内容
| 出題内容 | 具体的な問い | 対策記事 |
|---|---|---|
| 分散分析表の穴埋め | 残差平方和 Se、分散比 F₀ を求めよ | 平方和の分解 |
| 回帰モデルの有意性 | F₀ と F表を比較して判定せよ | F検定 |
| 偏回帰係数の検定 | β₁=0、β₂=0 は棄却されるか？ | t検定 |
| 偏回帰係数の区間推定 | β₁ の99%信頼区間を求めよ | 区間推定 |
| 切片の推定 | 切片 β₀ の推定値を求めよ | 正規方程式 |
QC検定では、「与えられた統計量から計算する」問題が多いです。公式を暗記するだけでなく、実際に手を動かして計算練習することが大切です。
よくある質問（FAQ）
A. 各変数の平方和・積和を求め、それを使った正規方程式（連立方程式）を解きます。説明変数同士が無相関なら、単回帰と同じくらい簡単に求まります。
A. 理論上は何個でも入れられますが、サンプル数に対して多すぎると過剰適合します。また互いに相関の強い変数を入れると多重共線性が起き、係数が不安定になるので注意が必要です。
A. 偏回帰係数は「他の変数を固定したときの純粋な影響度」を表します。単回帰の回帰係数は他の変数を無視しているため、値が変わることがあります。
A. できます。「データ分析」アドインの「回帰分析」機能で、偏回帰係数・決定係数・分散分析表まで自動で出力されます。手計算で仕組みを理解してから使うと、結果を正しく読めます。
📋 まとめ
この記事では、重回帰分析の基本的な考え方を解説しました。
- 重回帰分析は、複数の説明変数から目的変数を予測する手法
- 単回帰との違いは、説明変数が1つか2つ以上か
- 偏回帰係数は「他の変数を固定したときの影響度」を表す
- 注意点として、多重共線性・相関≠因果・外挿の危険がある
- QC検定では、分散分析表・F検定・t検定・区間推定が頻出
重回帰分析は、単回帰分析の「進化版」です。基本的な考え方は同じなので、単回帰をしっかり理解していれば、重回帰もスムーズに理解できます。
次は、「偏回帰係数」の意味をもっと深く理解しましょう。
📚 次に読むべき記事
重回帰分析の最重要概念を深掘り
実際に手を動かして係数を計算する
QC検定頻出の分散分析表を攻略
【超入門】回帰分析とは？「未来を予測する」仕組みを小学生でもわかるように解説 →
この記事を書いた人
シラス｜メーカー現役エンジニア
30代のメーカーエンジニア。実務で統計学・回帰分析・実験計画法・信頼性工学を日常的に使い、製品の品質改善やデータ分析を担当。保有資格はQC検定、電気主任技術者（電験三種）など。「専門知識を、誰にでもわかる言葉で」をモットーに、当ブログ「soloblog」で技術系記事を体系的に発信しています。
この記事の数値例は、市販の教科書を引き写したものではなく、筆者が実際にExcelと電卓で計算し、つまずいた過程も含めて掲載しています。